Материал из РУВИКИ — свободной энциклопедии

Решётчатая модель

Решётчатая модель
англ. lattice model
Область использования Финансовая математика
Дата появления 1979 год
Автор понятия Джон Кокс, Стивен Росс, Марк Рубинштейн

В современной финансовой математике решётчатая моде́ль (англ. lattice model)[1] — численный метод оценки стоимости производных финансовых инструментов, применимым в ситуациях, когда необходим пошаговый анализ временного процесса. Наиболее распространённый пример использования данной модели — оценка американских опционов на акции с дивидендами, когда инвестор вправе досрочно закрыть позицию в любой рабочий день до истечения срока опционного контракта.

Биномиальная решётка для акций с формулами CRR
Решётка для (встроенного) опциона на облигацию, иллюстрирующая опционно-скорректированный спред: верхнее значение в узле — краткосрочная ставка (выделена чёрным); динамика стоимости облигации (выделена красным) наглядно демонстрирует эффект подтягивания к номиналу

Классические непрерывные модели, такие, как модель Блэка — Шоулза, способны оценивать только европейские опционы, исполняемые строго в установленный срок экспирации.

Помимо прочего, решётчатые модели получили распространение при анализе процентных деривативов, поскольку позволяют эффективно учитывать искажения, вызванные недостатками непрерывных моделей, включая явление подтягивания к номиналу (англ. pull-to-par)[2], когда цена облигации по мере приближения срока погашения постепенно приближается к своему номиналу.

Метод особенно полезен при расчёте цен экзотических опционов, поскольку позволяет учитывать зависимость выплаты от динамики цен базового актива. Хотя классический метод Монте-Карло эффективен для простых инструментов, он имеет ограничения при учёте решений владельцев опционов о досрочном закрытии опционных контрактов[3]. Однако современные модификации метода Монте-Карло позволяют частично компенсировать этот недостаток и повысить точность оценки стоимости.

Производные финансовые инструменты на акции и товары

[править | править код]
Оценка опциона на акции с использованием древовидной (решётчатой) модели:

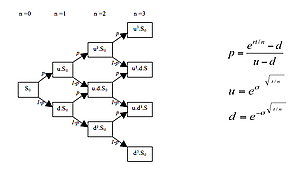
Шаг 1. Построение дерева цен акций одним из двух способов:

  • последовательное построение, при котором к текущей цене применяется повышающий () либо понижающий () коэффициент, так что на следующем временном шаге цена станет либо либо ;
  • если дерево является рекомбинирующим (то есть последовательность вверх-вниз приводит к той же цене, что и вниз-вверх), можно сразу вычислить цену в любом узле напрямую через формулу , где — количество шагов вверх и — количество шагов вниз.

Шаг 2. Построение соответствующего дерева опциона:

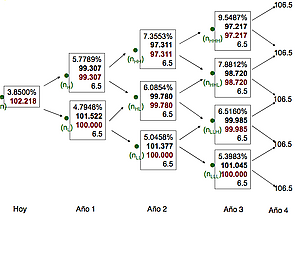
  • на каждом конечном узле дерева (то есть в момент истечения срока действия опциона) стоимость опциона равна просто его внутренней стоимости, или стоимости исполнения;
  • на более ранних узлах стоимость определяется через ожидание: , где  — вероятность роста цены. Для американских опционов стоимость в узле равна наибольшему из двух значений: расчётной ожидаемой стоимости (при продолжении владения опционом) или стоимости его немедленного исполнения при соответствующей цене акции в этом узле

В целом, алгоритм оценки опционов на акции и товары с помощью решётчатых моделей заключается в следующем: промежуток времени между текущим моментом и датой экспирации опциона делится на N дискретных временных шагов. На каждом временном интервале n модель описывает конечное число исходов на следующий шаг n + 1, таким образом охватывая в отдельной ветви каждую возможную вариацию изменения рыночной ситуации между этими двумя временными отметками. Этот процесс повторяется последовательно до тех пор, пока не будут учтены все возможные пути развития событий от начального периода n=0 до финального периода n=N. Затем оцениваются вероятности для каждого пути от n до n + 1. Эти значения вместе с итоговыми результатами перемещаются обратно по дереву до достижения корня, обеспечивая расчёт справедливой стоимости опциона на настоящий момент времени.

Варианты оценки европейских опционов на акции и товары[править | править код]

Для европейских опционов на акции и товары подход выглядит следующим образом:

Как уже отмечалось ранее, решётчатая модель особенно полезна при оценке американских опционов, где решение о досрочном исполнении опциона или удержании его до окончания срока может быть смоделировано для каждой отдельной комбинации времени и цены; это также верно и для бермудских опционов. По аналогичным причинам реальные опционы и опционы эмитента часто оцениваются с использованием решётчатого метода, хотя и с модифицированными допущениями. В каждом из вышеназванных случаев требуется третий шаг — на каждом узле решается, подлежит ли опцион исполнению или остаётся открытым, и соответствующая стоимость фиксируется на рассматриваемом узле дерева.

Некоторые экзотические опционы, такие как барьерные опционы, также легко моделируются с помощью этого подхода. Однако для других опционов, зависящих от истории цены, предпочтительны методы имитационного моделирования (например, метод Монте-Карло), хотя имеются и специализированные адаптации решётчатых методов для таких ситуаций[5][6].

Самой простой решётчатой моделью является биномиальная модель ценообразования опционов[7]; стандартный («канонический»)[8] метод был предложен в 1979 году Джоном Каррингтоном Коксом (англ. John Carrington Cox), Стивеном Россом (англ. Stephen Ross) и Марком Рубинштейном (англ. Mark Rubinstein) и получил название «биномиальная модель CRR»; формула приведена на диаграмме.

Позднее появились более двадцати альтернативных методов[9], каждый из которых построен на собственных предположениях о динамике изменения цены базового актива[4]. При росте числа временных шагов, эти модели постепенно приближаются в пределе к логнормальному распределению и, следовательно, дают ту же цену опциона, что и модель Блэка — Шоулза. Для достижения этого различные методы стремятся согласовать измеренные дискретно центральные моменты, начальные (или сырые) моменты и/или лог-моменты базового актива на каждом временном шаге. Новые усовершенствования нацелены на повышение устойчивости модели относительно модели Блэка — Шоулза при изменении числа временных шагов. Фактически современные модели проектируются с целью непосредственной сходимости к решению модели Блэка — Шоулза[9].

Разновидностью биноминальной модели является триномиальное дерево[10][11], которое в 1986 году предложил ирландский экономист Фелим Бойл (англ. Phelim Boyle). В отличие от биноминальной модели, где цена актива может двигаться только вверх или вниз, в триномиальном подходе добавляется ещё одна возможность — сохранение текущей цены. Таким образом, стоимость опциона оценивается на основании трёх потенциальных путей развития события на следующем временном шаге: рост, падение и стабилизация.

Подобно биноминальной модели, для триномиального подхода существует похожий (хотя и немного меньший по числу) набор методов оценки. При небольшом количестве временных шагов триномиальная модель даёт более точные результаты[12], чем биноминальная, и поэтому используется там, где критична скорость вычислений или ограничены вычислительные ресурсы. Для классических ванильных опционов увеличение числа шагов приводит к быстрому сближению результатов обеих моделей, и тогда биномиальная модель является предпочтительной из-за более простой реализации. Однако для экзотических опционов триномиальная модель (или её адаптации) иногда оказывается более стабильной и точной независимо от размера шага.

Для опционов с несколькими базовыми активами — например, радужного или корзинного — могут быть построены «мультиномиальные решётки»[13]. В данном варианте решётчатой модели каждый базовый актив будет иметь собственное дерево и стоимость опциона в каждом узле будет функцией соответствующих узлов на всех деревьях базовых активов. В случае двух активов такое дерево будет называться биномиальной пирамидой[13]. Здесь возникают две дополнительные сложности[14]: во-первых, количество узлов увеличивается экспоненциально с числом базовых активов; во-вторых, в этих продуктах значительную роль играет корреляция между активами, и она также должна учитываться при моделировании.

Измерение и управление рисками[править | править код]

Различные греки (показатели чувствительности) можно оценить непосредственно на решётке, где сами показатели вычисляются методом конечных разностей[15]. Например:

Дельта () и гамма Гамма () (чувствительности стоимости опциона к изменению цены актива) приблизительно определяются разницей в стоимости опциона, связанной с изменением уровня цены актива в одном и том же временном шаге. Тета () (чувствительность к течению времени) оценивается на основе разницы между стоимостью опциона на первом узле дерева и стоимостью того же опциона в последующей временной точке (на втором временном шаге для триномиальной модели, на третьем — для биномиальной. Заметим, что если коэффициент снижения () не равен обратному значению коэффициента роста (), этот способ оценки теты может потерять точность).

Что касается других греков, то измерения Ро () (чувствительности к процентной ставке) и Веги () (чувствительности к подразумеваемой волатильности) являются косвенными, так как стоимость опциона должна быть повторно рассчитана на новом дереве, построенном с незначительно изменёнными ставками или уровнем волатильности. Величина чувствительности определяется путём вычисления конечных разностей между первоначальными и новыми значениями. Также интересен показатель фугит (англ. fugit) — приблизительное время до исполнения американского опциона, которое обычно вычисляют с использованием методов на основе решёток.

После кризиса 1987 года, а особенно после финансового кризиса 2008 года, появилась необходимость учитывать в моделях ценообразования эффект улыбки волатильности (для разных уровней страйков) и поверхности волатильности (включающей также сроки экспирации). Это связано с осознанием того, что распределение колебаний цен базового актива неоднородно по срокам до экспирации (это явление известно как срочная структура волатильности) и не соответствует нормальному распределению, как это предполагается в модели Блэка — Шоулза; более подробно этот вопрос рассматривается в разделах Финансовая математика § Критика и Оценка опционов § Переосмысление моделей ценообразования опционов после кризиса 2008 года. Чтобы учесть эти особенности, банки перешли к применению стохастических или локальных моделей волатильности[16]. В рамках решётчатой методики строят так называемые вменённые деревья (англ. implied trees), которые фактически представляют собой дискретизацию указанных моделей. Такие деревья строятся так, чтобы идеально воспроизводить существующие рыночные цены опционов с различными страйками и сроками экспирации, гарантируя рынку соответствие теоретических цен европейским опционам (причём соответствие сохраняется для всех узлов дерева)[17]. Используя откалиброванную решётку, можно затем оценить опционы с комбинациями страйков и сроков, не котируемых на рынке, причём полученные цены будут согласованы с наблюдаемым поведением волатильности. Что касается управления рисками, то калибровка повышает точность «греков», то есть показателей чувствительности инструмента к ключевым факторам, влияющим на его стоимость.

Существует как биноминальный вариант вменённого дерева (часто называемый IBT Рубинштейна, или R-IBT (англ. implied binominal tree))[18], так и триномиальные вариант (известный как модель Дермана — Кани — Криса [DKC])[17]; она заменила собой DK-IBT[19]. DKC, по сути, является дискретизированной реализацией модели локальной волатильности.

Первая модель (биноминальное дерево R-IBT) проще в построении, но согласуется только с одним сроком погашения. Триномиальное дерево (DKC) согласовано сразу со всеми сроками и узлами, но требует наличия известных (или интерполированных) цен на каждом шаге и узле. Процесс построения подразумевает следующее:

В модели R-IBT первым шагом является восстановление вменённых конечных риск-нейтральных вероятностей для текущих цен актива. Затем, исходя из допущения, что все пути, ведущие к одному и тому же конечному узлу, имеют одинаковую риск-нейтральную вероятность, каждому конечному узлу присваивается «вероятность пути». После этого процесс упрощённо сводится к трём шагам: трёхэтапная обратная рекурсия позволяет восстановить вероятности узлов для каждого временного шага. Оценка опциона далее проводится стандартным способом и использует эти вероятности вместо изначального параметра .

В модели DKC первым шагом является восстановление цен состояний (англ. state prices), соответствующих каждому узлу дерева, таким образом, чтобы они согласовывались с наблюдаемыми ценами опционов (то есть с поверхностью волатильности). После этого для каждого узла находятся вероятности движения вверх, вниз и посередине (последнее — минимальное изменение или полная стабильность цены) так, чтобы:

  • суммы вероятностей равнялись единице;
  • цены смежных временных шагов следовали риск-нейтральному движению, учитывающему дивидендную доходность;
  • цены состояний «росли» на уровне безрисковой ставки[20].

Решение здесь является итеративным для каждого временного шага, а не одновременным для всего дерева. Далее, как и в случае с R-IBT, оценка опциона проводится стандартным методом обратной рекурсии.

В качестве альтернативы можно построить биноминальные деревья Эджворта (англ. Edgeworth binomial trees)[21], основанные на теории ряда Эджворта, которые позволяют аналитикам самостоятельно задавать требуемые значения асимметрии (англ. skew) и эксцесса (англ. kurtosis) (меры крутизны хвостов распределения) в колебаниях спотовых цен. В результате опционы с разными страйками покажут различные вменённые волатильности и дерево можно откалибровать к «улыбке волатильности» путём оптимального выбора параметров[22]. При оценке американских опционов стоимость будет определяться на основе биноминального варианта вменённого дерева (R-IBT), сочетаемого с откалиброванным распределением по срокам. Однако подход Эджворта ограничен в отношении набора пар асимметрии и эксцесса, для которых доступны правильные (валидные) распределения. В связи с этим более новые биномиальные деревья Джонсона[23] используют семейство распределений Джонсона, так как оно cпособно поддерживать любые пары значений асимметрии и эксцесса. Деревья Эджворта (или Джонсона) также полезны для других задач, где поведение базового актива существенно отклоняется от нормального распределения. В частности, их можно применить к мультиномиальным опционам (например, к корзиночным), используя аппроксимирующее распределение[24], которое формирует конечные узлы дерева и соответствующие уровни асимметрии и эксцесса.

Моделирование рисков с учётом поправки на кредитную стоимость (англ. Credit Valuation Adjustment, CVA) и иных корректировок стоимости деривативов (англ. X-Valuation Adjustment, XVA) с помощью решётчатых методов будет рассмотрено ниже.

Производные инструменты, привязанные к процентным ставкам

[править | править код]
Оценка опциона на облигации с использованием древовидной (решётчатой) модели:

Шаг 0. Построение дерева процентных ставок, согласованного с текущей кривой доходности.

Шаг 1. Построение дерева цен облигаций, где базовая облигация оценивается в каждом узле с помощью обратной индукции:

  • в конечных узлах стоимость облигации — просто номинальная стоимость (или 1 доллар) плюс купон (если предусмотрен); если дата облигации и дата узла дерева не совпадают, эти суммы дисконтируются к началу временного шага, используя краткосрочную ставку, специфичную для данного узла;
  • в каждом более раннем узле стоимость представляет собой дисконтированное ожидаемое значение узлов на более позднем временном шаге, с использованием вероятностей и из модели, плюс купонные платежи за текущий временной шаг, также дисконтированные к началу временного шага.

Шаг 2. Построение соответствующего дерева опционов на облигации, где стоимость опциона определяется аналогично оценке опционов на акции:

  • на дату экспирации опциона стоимость основывается на внутренней стоимости для всех узлов в этом временном шаге;
  • на более ранних узлах стоимость опциона равна дисконтированному ожидаемому значению стоимости опциона на следующем временном шаге, где дисконтирование производится по краткосрочной ставке текущего узла. Для американских опционов стоимость в узле равна наибольшему из двух значений: расчётной ожидаемой стоимости (при продолжении владения опционом) или стоимости его немедленного исполнения при соответствующей цене облигации в этом узле

Решётки обычно используются для оценки стоимости опционов на облигации, свопционов и других процентных производных инструментов[25][26].

В этих случаях оценка во многом схожа с описанной выше, но требует дополнительного, нулевого шага: построения дерева процентных ставок, на котором затем основывается цена базового актива. Следующий шаг также отличается: цена базового актива здесь строится с помощью обратной индукции (то есть движется в обратном направлении от даты погашения, накапливая приведённую стоимость запланированных денежных потоков в каждом узле), в отличие от прямого движения вперёд от даты оценки, как это было описано ранее.

Затем финальный шаг — оценка самого опциона — выполняется стандартным образом.

Подходы[править | править код]

Исходная решётка строится путём дискретизации либо модели краткосрочной ставки (например, модели Халла — Уайта или модели Блэка — Дэрмана — Тоя), либо модели форвардной ставки (такой как модели LIBOR или модели Хита — Джарроу — Мортона). Как и для акций, для этих моделей также могут применяться триномиальные деревья[27]; обычно это относится к деревьям Халла — Уайта.

В рамках модели Хита — Джарроу — Мортона[28] условие отсутствия арбитража подразумевает существование меры вероятности мартингала, а также определённых ограничений на коэффициенты дрейфа (англ. drift coefficients) форвардных ставок. Эти коэффициенты, в свою очередь, зависят от волатильности(ей) форвардных ставок[29]. Простое дискретное выражение для дрейфа[30] позволяет представить форвардные ставки в биноминальной решётке. Для этих моделей, основанных на форвардных ставках, древовидная структура может не сходиться[31][28] (это означает, что последовательность движений вверх-вниз даёт иной результат, нежели последовательность движений вниз-вверх). В таких случаях дерево иногда называют кустообразным (англ. bush), и число узлов растёт экспоненциально с ростом числа временных шагов. Альтернативой является подход с использованием биноминального дерева с рекурсивным соединением, реализованный в модели рынка LIBOR, который сохраняет свойство комбинирования узлов[32].

В свою очередь модели краткосрочной ставки подразделяются на равновесные (англ. equilibrium-based) (например, модель Васичека и CIR-модель) и свободные от арбитража (англ. arbitrage-free) (например, модель Хо — Ли и последующие). Различия заключаются в следующем[33]:

  • в равновесных моделях кривая доходности выводится из самой модели;
  • в моделях, свободных от арбитража, кривая доходности является входным параметром.

Подход равновесных моделей заключается в том, чтобы «калибровать» параметры таким образом, чтобы цены облигаций, полученные моделью в её непрерывной форме, наилучшим образом соответствовали наблюдаемым рыночным ценам[34]. Затем дерево строится как функция этих параметров. В случае свободных от арбитража моделей калибровка выполняется непосредственно на решётке: требуется добиться соответствия как текущей структуре процентных ставок (кривой доходности), так и соответствующей структуре волатильности. Здесь калибровка означает, что дерево процентных ставок воспроизводит цены бескупонных облигаций и любых других чувствительных к ставке ценных бумаг, которые использовались при построении кривой доходности. Подобный подход напоминает создание вменённых деревьев для акций, рассмотренных выше, и схож с техникой бутстрэппинга, которая применяется в финансах для реконструкции кривой доходности по доступным рыночным инструментам.

Для моделей, предполагающих нормальное распределение (например, модель Хо — Ли), калибровка может выполняться аналитически, в то время как для логнормальных моделей используется числовой метод нахождения корней уравнений (англ. root-finding algorithm).

Структура волатильности — иными словами, вертикальное расстояние между узлами — отражает волатильность ставок за квартал или другой период, соответствующий временному шагу решётки. Некоторые аналитики предпочитают использовать «реализованную волатильность», то есть историческую волатильность ставок для указанного временного шага. Однако большинство предпочитает придерживаться рыночно-консервативной практики и использует текущие рыночные цены на кэпы процентной ставки (англ. interest rate caps) и вменённую волатильность для ценообразования каждого компонентного кэплета (англ. caplet) по модели Блэка. Данная функциональная связь с волатильностью определяет существенные отличия в построении дерева процентных ставок по сравнению с вменённым деревом для акций: для процентных ставок волатильность известна для каждого временного шага (она задаётся структурой волатильности рынка) и значения узлов (то есть сами процентные ставки) должны быть рассчитаны для заданных риск-нейтральных вероятностей. Для акций, напротив, единую волатильность нельзя задать для каждого временного шага (эффект улыбки волатильности), и дерево строится путём расчёта вероятностей, соответствующих заданным значениям базового актива в каждом узле.

После калибровки решётка процентных ставок используется для оценки различных инструментов с фиксированным доходом и производных от них[28]. Описание подхода для опционов на облигации дано в описании справа — стоит отметить, что указанный подход решает проблему подтягивания к номиналу, характерную для закрытых аналитических методов. Логика оценки свопционов почти идентична описанной ранее, но вместо облигаций на шаге 1 рассматриваются свопы, а на шаге 2 вместо опционов на облигации — свопционы. Для кэпов (англ. caps) и флооров (англ. floors) шаги 1 и 2 объединены: стоимость на каждом узле определяется на основе значений соседних узлов в следующем временном шаге, а для каждого истекающего кэплета или флорлета прибавляется произведение разницы между контрактной фиксированной ставкой и текущей краткосрочной ставкой на данном узле, скорректированное на долю дня (по правилу расчёта временных интервалов) и номинальную сумму контракта. Для облигаций с правом отзыва (англ. callable) и досрочного погашения (англ. putable) потребуется третий шаг: прежде чем делать шаг назад во времени на каждом узле временного шага необходимо учесть влияние встроенного опциона на цену облигации и/или цену опциона (отметим, что эти опционы не являются взаимоисключающими, и поэтому облигация может иметь несколько встроенных опционов[35]; гибридные ценные бумаги рассматриваются ниже). Для других, более экзотических процентных производных инструментов аналогичные корректировки вносятся в шаг 1 и далее. Для вычисления греков (показателей чувствительности) применима та же логика, как и для акций (см. следующий раздел).

Альтернативный подход к моделированию американских опционов на облигации (в частности, тех, страйк которых привязан к доходности к погашению) использует модифицированные методы решёток для акций[36]. В этом случае аналитик строит CRR-дерево доходности к погашению, применяя допущение о постоянной волатильности, а затем рассчитывает цену облигации как функцию этой доходности в каждом узле — таким образом полученные цены демонстрируют тенденцию подтягивания к номиналу. Второй шаг заключается в том, чтобы затем учесть любую срочную структуру волатильности путём построения соответствующего DKC-дерева (основанного на каждом втором временном шаге в CRR-дереве, поскольку DKC является триномиальным, а CRR — биномиальным). Затем это дерево используется для оценки стоимости опциона.

Изменения в оценке после кризиса 2008 года[править | править код]

После финансового кризиса 2008 года оценка свопов стала происходить преимущественно в рамках так называемого подхода с несколькими кривыми (англ. multi-curve framework) вместо традиционного подхода с одной общей кривой процентных ставок (чаще всего LIBOR); подробнее см. статью Процентный своп § Ценообразование. Выплаты устанавливаются в зависимости от базисной ставки LIBOR, соответствующей нужному сроку, а дисконтирование осуществляется по ставке межбанковского овернайта (англ. overnight indexed swap (OIS)), признанной новой стандартной безрисковой ставкой[37]. Чтобы внедрить новую систему оценки в решётчатую модель, обе ставки — OIS и LIBOR — моделируются совместно в трёхмерном дереве, построенном таким образом, чтобы обеспечить совпадение полученных цен свопов с рыночными ценами свопов по OIS и LIBOR при сохранении корреляции между обоими видами ставок[38]. Достигнув нулевого шага, дальнейшая оценка проходит аналогично предыдущей схеме, начиная с шага 1, но теперь денежные потоки основываются на дереве LIBOR, а дисконтирование — на соответствующих узлах дерева OIS (аналогично описанному выше подходу с пирамидами).

Ещё одно изменение связано с тем, что банки вводят поправки на кредитный риск (CVA) и другие виды поправок (XVA) при оценке контрактов на производные инструменты. Цель этих поправок двояка: с одной стороны, это защита от возможных убытков, вызванных неспособностью контрагентов платить по контрактным обязательствам, а с другой — определение (и хеджирование) необходимого капитала банка согласно требованиям достаточности капитала. Хотя обычно такие поправки рассчитываются с помощью имитационного компьютерного моделирования, в ряде случаев можно использовать и решётчатые методы[39][40][41].

Например, в случае свопа[39] потенциальная будущая экспозиция (англ. potential future exposure (PFE)) банка на каждую дату представлена как средневзвешенное значение положительных выплат и стоимости свопа по всем узлам дерева на указанную дату. Вероятность каждого узла, в свою очередь, является функцией кумулятивных вероятностей повышения и понижения дерева. Затем PFE объединяется с внешней для дерева вероятностью дефолта контрагента и коэффициентом возмещения контрагента для вычисления ожидаемого убытка на эту дату. Наконец, агрегированная приведённая стоимость этих потерь составляет размер CVA для банка по данному контрагенту и позиции.

Гибридные ценные бумаги

[править | править код]

Гибридные ценные бумаги, сочетающие черты как акций, так и облигаций, также оцениваются с помощью деревьев[42]. Один из подходов к оценке конвертируемых облигаций, предложенный в 1998 году американскими специалистами Костасом Циверйотисом (англ. K. Tsiveriotis) и Крисом Фернандесом (англ. C. Fernandes)[43], заключается в том, чтобы разделить стоимость облигации на каждом узле на две составляющие: «акционную» компоненту, обусловленную ситуациями, когда облигация будет конвертирована в акции, и «долговую» компоненту, связанную с ситуациями, когда облигация будет погашена. Соответственно, создаются два параллельных дерева — в одном дисконтирование производится по безрисковой ставке (для долевой компоненты), а в другом — по ставке, скорректированной на кредитный риск (для долговой компоненты); сумма стоимостей этих двух компонент на каждом узле и представляет собой итоговую стоимость конвертируемой облигации[44]. Существуют и другие методы, использующие сочетание дерева акций и дерева коротких ставок[45]. Альтернативный подход, первоначально предложенный инвестиционным банком Goldman Sachs в 1994 году[46], не отделяет компоненты друг от друга. Вместо этого дисконтирование осуществляется по взвешенной по вероятности конвертации безрисковой и рискованной процентной ставке внутри одного дерева.

В широком смысле акции компаний можно рассматривать как колл-опцион на фирму[47]: если стоимость фирмы оказывается ниже объёма долговых обязательств, владельцы акций отказываются оплачивать долг и инициируют процедуру ликвидации (то есть осуществляют своё право по опциону). Если компания способна своевременно обслуживать долг, акционеры принимают решение о погашении обязательств[48]. Решётчатые модели применяются для анализа акций[49], особенно в компаниях, переживающих кризисные времена[50]. Практика рассмотрения акций как опциона получила распространение в США, где юридические нормы регулируют ответственность акционеров и процедуры банкротства[51]. Российское законодательство (Федеральный закон № 127-ФЗ «О несостоятельности (банкротстве)») также регламентирует взаимоотношения между ограниченной ответственностью акционеров и процедурой банкротства. Решётчатые модели широко применяются для анализа корпоративных долговых обязательств, особенно в условиях нестабильной рыночной среды или кризиса. Данные модели позволяют учитывать специфику российского правового поля и корректно оценивать кредитные риски[52].

Расчёт греков для процентных деривативов осуществляется так же, как и для инструментов на акции. Но существует дополнительная специфика, особенно важная для гибридных ценных бумаг: требуется оценить чувствительность к общим изменениям процентных ставок. Для облигаций с встроенными опционами стандартные методы расчёта длительности и выпуклости, основанные на доходности к погашению, не учитывают, как изменения процентных ставок повлияют на денежные потоки из-за исполнения опционов. Для решения этой проблемы вводятся понятия эффективной дюрации (англ. effective duration) и эффективной выпуклости (англ. effective convexity). Расчёт аналогичных показателей чувствительности, таких как Ро () и Вега (), проводится следующим образом: сначала дерево процентных ставок перестраивается дважды — один раз при параллельном повышении, а затем при параллельном снижении всей кривой доходности. Затем, исходя из соответствующих изменений стоимости облигации, интересующие нас греки рассчитываются численными методами[53].

Примечания

[править | править код]
  1. ↑ Investopedia Staff. Lattice-Based Model (17 ноября 2010).
  2. ↑ Hull, J. C. Options, futures, and other derivatives. — 9. — Pearson Education, 2015. — ISBN 0-13-345631-5.
  3. ↑ Cox, J. C., Ross, S. A., & Rubinstein, M. Option pricing: A simplified approach // Journal of Financial Economics. — 1979. — № 7(3). — С. 229–263.
  4. ↑ 1 2 Chance, Don M. A Synthesis of Binomial Option Pricing Models for Lognormally Distributed Assets (англ.) // Journal of Applied Finance. — 2008. — Vol. 18. Архивировано 4 марта 2016 года.
  5. ↑ Timothy Klassen. Simple, fast and flexible pricing of Asian options (англ.) // The Journal of Computational Finance. — 2001. — Vol. 4, iss. 3. — P. 89–124. — ISSN 1460-1559. — doi:10.21314/jcf.2001.067.
  6. ↑ John Hull and Alan White. Efficient procedures for valuing European and American path-dependent options . Fall 1993. 21–31. (англ.) // Journal of Derivatives. — 1993. — P. 21–31. — doi:10.3905/jod.1993.407869.
  7. ↑ Ronald Becker. Pricing in the Binomial Model. — African Institute for Mathematical Sciences. Архивировано 29 ноября 2015 года.
  8. ↑ Prof. Markus K. Brunnermeier. «Multi-period Model Options», Princeton University.
  9. ↑ 1 2 Mark S. Joshi (2008). «The Convergence of Binomial Trees for Pricing the American Put» Архивировано 2 июля 2015 года.
  10. ↑ Mark Rubinstein. On the Relation Between Binomial and Trinomial Option Pricing Models // The Journal of Derivatives. — 2000-11-30. — Т. 8, вып. 2. — С. 47–50. — ISSN 2168-8524 1074-1240, 2168-8524. — doi:10.3905/jod.2000.319149.
  11. ↑ Zaboronski et al (2010). Pricing Options Using Trinomial Trees. University of Warwick
  12. ↑ Option Pricing & Stock Price Probability Calculators – Hoadley. hoadley.net.
  13. ↑ 1 2 Rubinstein, Mark «Somewhere over the rainbow.» Risk 4.11 (1991): 61-63.
  14. ↑ Staff (2024). The Multi-Asset Binomial-Model, fastercapital.com
  15. ↑ D. M. Chance. CALCULATING THE GREEKS IN THE BINOMIAL MODEL. http://www.bus.lsu.edu/academics/finance/faculty/dchance/Instructional/ (14 января 2005).
  16. ↑ А. Смирнов. Анализ различных методов оценки исторической волатильности для опционной торговли // Международный научно-исследовательский журнал. — 2016. — Т. 9 (51). — С. 78—80.
  17. ↑ 1 2 Emanuel Derman, Iraj Kani, and Neil Chriss (1996). Implied Trinomial Trees of the Volatility Smile. Goldman Sachs, Quantitative Strategies Research Notes
  18. ↑ Mark Rubinstein (1994). Implied Binomial Trees. Journal of Finance. July 1994.
  19. ↑ Emanuel Derman and Iraj Kani (1994). The Volatility Smile and Its Implied Tree. Research Note, Goldman Sachs.
  20. ↑ Jim Clark, Les Clewlow, Chris Strickland. August 2008 // Energy Risk. — 2008. — Август. — С. 61—65. Архивировано 25 ноября 2025 года.
  21. ↑ Mark Rubinstein (1998). Edgeworth Binomial Trees. Journal of Derivatives, Spring 1998.
  22. ↑ Mary Jackson, Mike Staunton. Advanced Modelling in Finance using Excel and VBA. — Wiley. — ISBN 0-471-49922-6.
  23. ↑ Jean-Guy Simonato (2011)., Quantitative Finance, Volume 11, Pages 1165-1176. Johnson binomial trees // Quantitative Finance. — 2011. — Т. 11, № 8. — С. 1165—1176. — doi:10.1080/14697680902950821.
  24. ↑ Isabel Ehrlich (2012). Pricing Basket Options with Smile. Thesis, Imperial College
  25. ↑ Martin Haugh. Term Structure Lattice Models (англ.). Columbia University (2010).
  26. ↑ S. Benninga and Z. Wiener. (1998).Binomial Term Structure Models, Mathematica in Education and Research. Vol.7 No.3
  27. ↑ M. Leippold, Z. Wiener. Efficient Calibration of Trinomial Trees for One-Factor Short Rate Models (англ.) (7 мая 2003).
  28. ↑ 1 2 3 Pricing Interest Rate-dependent Financial Claims with Option Features, Ch 11. in Rendleman (2002), per Bibliography.
  29. ↑ Prof. Don Chance, Louisiana State University. The Heath-Jarrow-Morton Term Structure Model Архивировано 23 сентября 2015 года.
  30. ↑ Dwight M Grant, Gautam Vora. Implementing No-Arbitrage Term Structure of Interest Rate Models in Discrete Time When Interest Rates Are Normally Distributed // The Journal of Fixed Income. — 1999-03-31. — Т. 8, вып. 4. — С. 85–98. — ISSN 2168-8648 1059-8596, 2168-8648. — doi:10.3905/jfi.1999.319247.
  31. ↑ Rubinstein, Mark. Rubinstein on Derivatives. — Risk Books, January 1, 1999. — ISBN 9781899332533.
  32. ↑ S. Derrick, D. Stapleton and R. Stapleton (2005). The Libor Market Model: A Recombining Binomial Tree Methodology
  33. ↑ Dr. Graeme West (January 2007). Interest Rate Derivatives
  34. ↑ Calibrating the Ornstein-Uhlenbeck (Vasicek) model. sitmo.com. Дата обращения: 19 июня 2015. Архивировано 19 июня 2015 года.
  35. ↑ embedded option. thefreedictionary.com.
  36. ↑ Riskworx (c. 2000). American Bond Option Pricing, riskworx.com
  37. ↑ John C. Hull, Alan White. Libor vs. OIS: The Derivatives Discounting Dilemma (англ.) // SSRN Electronic Journal. — 2012. — ISSN 1556-5068. — doi:10.2139/ssrn.2211800.
  38. ↑ John Hull, Alan White. Multi-curve Modelling Using Trees (англ.) // Springer Proceedings in Mathematics & Statistics. — Cham: Springer International Publishing, 2016. — P. 171–189. — ISBN 978-3-319-33445-5, 978-3-319-33446-2. — doi:10.1007/978-3-319-33446-2_9.
  39. ↑ 1 2 Donald J. Smith. [http://www.na-businesspress.com/JAF/SmithDJ_Web16_8_.pdf Understanding CVA, DVA, and FVA: Examples of Interest Rate Swap Valuation] // Journal of Accounting and Finance. — 2016. — Т. Vol. 16, № 8. — С. 11—31.
  40. ↑ Laura Ballotta, Gianluca Fusai, Marina Marena. A Gentle Introduction to Default Risk and Counterparty Credit Modelling // SSRN Electronic Journal. — 2016. — ISSN 1556-5068. — doi:10.2139/ssrn.2816355.
  41. ↑ Wujiang Lou. Derivatives Discounting Explained // SSRN Electronic Journal. — 2017. — ISSN 1556-5068. — doi:10.2139/ssrn.3092447.
  42. ↑ Pricing Convertible Bonds.
  43. ↑ Kostas Tsiveriotis, Chris Fernandes. Valuing Convertible Bonds with Credit Risk // The Journal of Fixed Income. — 1998-09-30. — Т. 8, вып. 2. — С. 95–102. — ISSN 2168-8648 1059-8596, 2168-8648. — doi:10.3905/jfi.1998.408243.
  44. ↑ Kurt Hess. Description of Tree Model for the Valuation of a Convertible Bond with Credit Risk. University of Waikato, Hamilton, New Zealand. Дата обращения: 12 июня 2015. Архивировано 21 марта 2012 года.
  45. ↑ D. R. Chambers, Qin Lu. A Tree Model for Pricing Convertible Bonds with Equity, Interest Rate, and Default Risk. Journal of Derivatives. Дата обращения: 31 мая 2007. Архивировано 21 апреля 2016 года.
  46. ↑ Emanuel Derman(1994). Valuing Convertible Bonds as Derivatives Quantitative Strategies Research Notes. Goldman Sachs.
  47. ↑ Aswath Damodaran (2002). Valuing Firms in Distress
  48. ↑ Нужденов А.Д. Современные методы оценки реальных опционов в оценке бизнеса // Аудит и финансовый анализ. — 2015. — Апрель. — С. 129—133.
  49. ↑ Grant Thornton Presentation (June 12, 2013). Valuation Considerations Related to Complex Financial Instruments for Investment Companies. Дата обращения: 8 июля 2015. Архивировано 9 июля 2015 года.
  50. ↑ Aswath Damodaran. Option Pricing Applications in Valuation
  51. ↑ Mark Broadie and Ozgur Kaya (2007). «A Binomial Lattice Method for Pricing Corporate Debt and Modeling Chapter 11 Proceedings», Journal of Financial and Quantitative Analysis, Vol. 42, No. 2
  52. ↑ Пономарева С.А. Применение биноминальной опционной модели в расчете стандартных издержек при проведении процедуры оценки регулирующего воздействия // Государственная Служба. — 2018. — Т. 20, № 5. — С. 56—61. — doi:10.22394/2070-8378-2018-20-5-56-61.
  53. ↑ Frank Fabozzi (1998). 3rd ed.).John Wiley. Valuation of fixed income securities and derivatives. — John Wiley & Son, 1998. — ISBN 978-1-883249-25-0.

Литература

[править | править код]
  • David F. Babbel. Valuation of Interest-Sensitive Financial Instruments. — 1st. — John Wiley & Sons, 1996. — ISBN 978-1883249151.
  • Gerald Buetow. Valuation of Interest Rate Swaps and Swaptions / Gerald Buetow, Frank Fabozzi. — John Wiley, 2000. — ISBN 978-1883249892.
  • Gerald Buetow. Term-Structure Models Using Binomial Trees / Gerald Buetow, James Sochacki. — The Research Foundation of AIMR (CFA Institute), 2001. — ISBN 978-0-943205-53-3.
  • Les Clewlow. Implementing Derivative Models / Les Clewlow, Chris Strickland. — New Jersey : Wiley, 1998. — ISBN 978-0-471-96651-7.
  • Tree methods in finance, Encyclopedia of Quantitative Finance / Rama Cont. — Wiley, 2010. — ISBN 978-0-470-05756-8.
  • Frank Fabozzi. Valuation of fixed income securities and derivatives. — 3rd. — John Wiley, 1998. — ISBN 978-1-883249-25-0.
  • Espen Haug. The Complete Guide to Option Pricing Formulas. — New York : McGraw-Hill, 2006. — ISBN 978-0-07-138997-6.
  • Richard Rendleman. Applied Derivatives: Options, Futures, and Swaps. — 1st. — Wiley-Blackwell, 2002. — ISBN 978-0-631-21590-5.
  • Mark Rubinstein. Rubinstein On Derivatives. — 1st. — Incisive Media Risk Books, 2000. — ISBN 978-1899332533.
  • Steven Shreve. Stochastic Calculus for Finance I: The Binomial Asset Pricing Model. — Springer, 2004. — ISBN 978-0387249681.
  • Donald J. Smith. Valuation in a World of CVA, DVA, and FVA: A Tutorial on Debt Securities and Interest Rate Derivatives. — World Scientific, 2017. — ISBN 978-9813222748.
  • John van der Hoek. Binomial Models in Finance / John van der Hoek, Robert J. Elliott. — Springer, 2006. — ISBN 978-0-387-25898-0.
Источник — https://ru.ruwiki.ru/w/index.php?title=Решётчатая_модель&oldid=1217482022