Броуновское движение

Экспертиза РАН

Проводится экспертиза
Российской академией наук

Подробнее

Экспертиза РАН

Проводится экспертиза
Российской академией наук

Подробнее

Материал ОГЭ/ЕГЭ

База знаний для подготовки к ЕГЭ и ОГЭ, проверенная Российской Академией наук

Подробнее

Материал ОГЭ/ЕГЭ

База знаний для подготовки к ЕГЭ и ОГЭ, проверенная Российской Академией наук

Подробнее

Бро́уновское движе́ние (англ. Brownian motion) — случайное движение частиц, взвешенных в среде (в жидкости или газе). Традиционное математическое описание броуновского движения основано на винеровском процессе, который даже в математических работах часто называют броуновским движением.

Такое движение характеризуется случайными флуктуациями положения частицы внутри подпрообласти среды, чередующимися с переходами в другие области. Каждое перемещение сопровождается дополнительными флуктуациями внутри нового замкнутого объёма. Такая картина отражает свойства среды при тепловом равновесии и фиксированной температуре. В подобной среде отсутствует предпочтительное направление движения (как в транспортных явлениях). Суммарный линейный и угловой импульсы среды в среднем равны нулю. Кинетические энергии молекулярных броуновских движений, а также вращательные и колебательные энергии молекул, вместе определяют калорическую составляющую внутренней энергии среды согласно теореме равнораспределения энергии.

Явление получило название в честь шотландского ботаника Роберта Брауна, который впервые описал его в 1827 году, наблюдая через микроскоп за пыльцой растения Clarkia pulchella, погружённой в воду. В 1900 году французский математик Луи Башелье в своей докторской диссертации «Теория спекуляции» под руководством Анри Пуанкаре смоделировал стохастический процесс, ныне известный как броуновское движение. В 1905 году физик-теоретик Альберт Эйнштейн опубликовал статью, в которой объяснил движение частиц пыльцы как результат ударов отдельных молекул воды, что стало одной из его первых крупных научных работ.

Случайный характер движения объясняется тем, что направление и сила ударов атомов постоянно меняются, и частица сталкивается чаще с одной стороны, чем с другой. Такое объяснение броуновского движения стало убедительным доказательством существования атомов и молекул, что было подтверждено опытами Жана Перрена в 1908 году. В 1926 году Перрен был удостоен Нобелевской премии по физике «за работу по дискретному строению материи».

Задача точного описания многих взаимодействующих тел, приводящих к броуновской картине, неразрешима аналитически; описывать явление можно лишь с помощью вероятностных моделей на основе статистических ансамблей. Классические модели статистической механики для броуновского движения были разработаны Эйнштейном и Смолуховским. Кроме того, броуновское движение описывается как частный случай стохастических процессов. Существует как более простые, так и более сложные последовательности стохастических процессов, предельным случаем которых становится броуновское движение.

Двумерное случайное блуждание атома серебра (адатом) на поверхности Ag(111)

Моделирование броуновского движения крупной частицы, аналогичной пылинке, сталкивающейся с большим числом малых частиц, аналогичных молекулам газа, движущихся с различными скоростями в случайных направлениях

История

Воспроизведено по книге Ж. Перрена, Les Atomes; три траектории движения коллоидных частиц радиусом 0,53 мкм, наблюдаемых под микроскопом. Положения через каждые 30 секунд соединены прямыми отрезками (размер сетки — 3,2 мкм).

В поэме римского философа и поэта Лукреция «О природе вещей» (около 60 года до н. э.) описано движение пыли в лучах света, что автор приводит как доказательство существования атомов:

Взгляни: когда луч солнца в полумрак проникнет,
Видишь, клубится в нём без числа мельчайших частичек,
Вечно в движенье они, в неослабном и странном танце...
Видим мы в этом движенье явный признак скрытых
Движений материи, что нашим глазам невидимы.
Оно начинается с атомов, движимых самих по себе.
Тогда мельчайшие тела, близкие к ним по строению,
Захвачены ими и движутся, сталкиваясь невидимо,
Эти же — сталкивают тела чуть крупнее себя,
Постепенно движенье становится зримым на свету —
Таковы отклонения мельчайших частиц, движимых невидимыми ударами...

Хотя наблюдаемое движение пыли во многом определяется токами воздуха, характерное мерцание и подёргивание малых частиц объясняется истинной броуновской динамикой; Лукреций фактически описал броуновское движение, однако сам пример был неточен.

Открытие явления обычно приписывают ботанику Роберту Брауну, который в 1827 году наблюдал под микроскопом за пыльцой Clarkia pulchella в воде. Частицы размером около 1/4000 дюйма совершали беспорядочные движения. Повторяя опыт с неорганическими частицами, Браун исключил возможность связи эффекта с проявлением жизни, хотя природа движения осталась неясной.

Математические основы стохастических процессов, в том числе броуновского движения, были введены Луи Башелье в 1900 году в его докторской диссертации о биржевых и опционных рынках. Однако эта работа была почти неизвестна до 1950-х годов.

Альберт Эйнштейн (в числе работ 1905 года) объяснил броуновское движение исходя из атомарного и молекулярного строения вещества, когда их существование ещё обсуждалось. Эйнштейн доказал связь вероятностного распределения броуновской частицы с уравнением диффузии. Его уравнения были подтверждены экспериментами Ж. Перрена в 1908 году, после чего в 1923 году Норберт Винер дал полное математическое описание броуновского движения — винеровский процесс.

В 2010 году впервые была экспериментально измерена мгновенная скорость броуновской частицы (стеклянной микросферы, захваченной оптическими пинцетами в воздухе), подтвердившая распределение Максвелла — Больцмана и теорему равнораспределения энергии для броуновской частицы.

Теории статистической механики

Теория Эйнштейна

Теория Эйнштейна состоит из двух частей: первый этап связан с выводом уравнения диффузии для броуновских частиц, где коэффициент диффузии связывается с средним квадратичным смещением частицы, второй этап — с выражением коэффициента диффузии через измеряемые физические параметры. Это позволило Эйнштейну определить размеры атомов и число атомов в моле вещества, то есть число Авогадро. Согласно закону Авогадро, этот объём одинаков для всех идеальных газов — 22,414 литра при стандартных условиях, а определение числа Авогадро эквивалентно определению массы атома через отношение молярной массы к постоянной Авогадро.

Типичные распределения (колоколообразные кривые) диффузии броуновских частиц. Начальное распределение — дельта-функция Дирака, со временем огибающая становится шире.

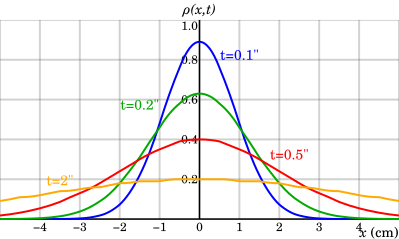
Эйнштейн рассмотрел изменение положения броуновской частицы за время $\tau$ в одномерном (x) пространстве и ввёл зависимость числа частиц $\rho (x,t)$ в окрестности x. Разложение функции в ряд Тейлора и симметрия задачи приводят к уравнению диффузии:

$${\frac {\partial \rho }{\partial t}}=D{\frac {\partial ^{2}\rho }{\partial x^{2}}}$$

с решением для начальных условий в виде нормального распределения:

$$\rho (x,t)={\frac {N}{\sqrt {4\pi Dt}}}\exp {\left(-{\frac {x^{2}}{4Dt}}\right)}$$

Среднеквадратическое смещение частицы: $\mathbb {E} {\left[x^{2}\right]}=2Dt.$ Отсюда смещение не пропорционально времени, а пропорционально квадратному корню из него.

Вторая часть теории связывает коэффициент диффузии с осреднённым смещением частицы и позволяет экспериментально определять число Авогадро и размеры молекул. Эйнштейн рассматривал динамическое равновесие противоположных по направлению потоков: например, в гравитационном поле частицы под действием силы тяжести оседают вниз, а диффузия стремится выравнивать концентрацию, перемещая их вверх. В равновесии скорости этих процессов равны, и можно записать: $D=\mu k_{\text{B}}T={\frac {\mu RT}{N_{\text{A}}}}={\frac {RT}{6\pi \eta rN_{\text{A}}}}$ где $\mu$ — подвижность частицы, $\eta$ — вязкость среды, $r$ — радиус частицы, $R$ — универсальная газовая постоянная, $T$ — абсолютная температура, и $N_{\text{A}}$ — постоянная Авогадро.

Экспериментальная проверка формулы Эйнштейна оказалась затруднительной. Лишь в 1908—1909 годах эксперименты Шодесега и Перрена подтвердили теорию, что стало важным эмпирическим подтверждением кинетической теории тепла.

Модель движения частицы красителя в воде (броуновское движение)

Модель Смолуховского

Смолуховский разработал альтернативную статистическую модель броуновского движения, получив то же распределение смещений частицы, что и Эйнштейн, но отличающийся множитель (27/64). Его подход объяснял, почему даже при равновероятных столкновениях влево-вправо суммарное смещение возрастает как корень из числа столкновений. Смолуховский также попытался объяснить, почему частица не ускоряется неограниченно, и показал, что в среднем её кинетическая энергия равна энергии окружающих молекул.

В 1906 году Смолуховский опубликовал одномерную модель для броуновского движения, которая, несмотря на простоту, дала качественное объяснение явления.

Уравнение Ланжевена

Уравнение Ланжевена служит более точной моделью эволюции положения частицы и учитывает случайные силы со стороны среды, отражая термические флуктуации. На больших временах динамику можно аппроксимировать броуновской динамикой.

Астрофизика: движение звёзд в галактиках

В звёздной динамике массивные объекты (звёзды, чёрные дыры) также могут испытывать броуновское движение под действием гравитационных сил от окружающих звёзд. Например, скорость броуновского движения сверхмассивной чёрной дыры Стрельца A* в центре Млечного Пути оценивается менее чем в 1 км/с.

Математическое описание

Пример двумерного случайного блуждания на торе. В пределе множества шагов процесс приближается к винеровскому.

В математике броуновское движение формализуется как винеровский процесс, непрерывный во времени стохастический процесс, введённый Норбертом Винером. Это один из наиболее известных процессов Леви (случайных процессов с независимыми и стационарными приращениями), встречающийся во многих разделах математики, экономики и физики.

Одна из реализаций трёхмерного броуновского движения на промежутке времени 0 ≤ t ≤ 2

Винеровский процесс W_t удовлетворяет свойствам:

1. 0
2. W_t почти наверное непрерывен
3. приращения W_t независимы
4. W_t - W_s \sim \mathcal{N}(0, t-s) для любых $0\leq s\leq t$

и является мартингалом с квадратичной вариацией t.

Винеровский процесс может быть построен как предельный случай случайного блуждания.

Модель броуновского движения описывает марковский процесс и задаётся стоxастическим интегральным уравнением.

См. также

• Случайное блуждание

Примечания

Литература

• Brown, Robert (1828). “A brief account of microscopical observations made in the months of June, July and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies” (PDF). Philosophical Magazine. 4 (21): 161—173. DOI:10.1080/14786442808674769. Архивировано из оригинала (PDF) 2022-10-09.
• Einstein, A. Investigations on the Theory of Brownian Movement. — New York : Dover, 1956. — ISBN 978-0-486-60304-9.
• Perrin, J. (1909). “Mouvement brownien et réalité moléculaire” [Броуновское движение и молекулярная реальность]. Annales de chimie et de physique. 8th series. 18: 5—114.
• von Smoluchowski, M. (1906). “Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen”. Annalen der Physik. 21 (14): 756—780. DOI:10.1002/andp.19063261405.
• Нельсон, Э. Dynamical Theories of Brownian Motion. (электронная версия).

Ссылки

• Броуновское движение в работах Эйнштейна (англ.)
• История, ботаника и физика открытий Броуна — с видеоматериалами (англ.)
• Наблюдение броуновской скорости — эксперимент (англ.)