Непрерывная функция

Термины непрерывность, непрерывный, разрывный в их современном смысле ввёл Коши, который привлёк понятие предела для формулировки непрерывности функции (1821). До него в эти слова вкладывалось другое значение. Эйлер, Лагранж, Фурье, Пуассон называли функцию непрерывной, если всюду в области определения она задана одним аналитическим выражением. В. Я. Буняковский ещё в 1839 году понимает непрерывность по Эйлеру, а для нового понятия — непрерывности по Коши — употребляет наименования «непрерывающаяся, сплошная линия», «сплошность». До этого в русской математике предлагалось название «разверзающиеся кривые».

Коши и Больцано писали о непрерывности функции на интервале. В рукописи Больцано (1830) содержится первое определение односторонней непрерывности. В статье 1875 года Дарбу дал определение непрерывности как локального свойства. Впервые Вейерштрасс дал определение в терминах ${\displaystyle \varepsilon -\delta }$ в 1861 году и с этого времени стал рассматривать свойства функций, непрерывных на замкнутом отрезке. Доказательства приобрели современный вид к 1874 году. Независимые исследования Дарбу относятся примерно к тем же годам.

Современное изложение в курсах математического анализа установилось после лекций Пеано (1884) и Жордана (1893). Стоит отметить, что до исследований Римана и Вейерштрасса непрерывные функции считались также и дифференцируемыми. В учебнике Дини (1878) впервые приведена классификация точек разрыва первого и второго рода. Вопрос о непрерывности функции нескольких переменных в точке впервые возник у Коши, который дал определение этому понятию в 1821 году. Но впоследствии оно было опровергнуто Стоксом (1848), Дюбуа-Реймоном (1869) и др. Современное определение непрерывности функции нескольких переменных в точке было дано Дарбу в 1872 году. Риман дал определение непрерывности функции комплексной переменной (1851)^[1].

Пусть точка ${\displaystyle a}$ принадлежит области задания функции ${\displaystyle f\{x\}}$ и любая ${\displaystyle \varepsilon }$-окрестность точки ${\displaystyle a}$ содержит отличные от ${\displaystyle a}$ точки области задания функции ${\displaystyle f\{x\}}$.

Функция ${\displaystyle f\{x\}}$ называется непрерывной в точке ${\displaystyle a}$, если функция ${\displaystyle f(x)}$ имеет в точке ${\displaystyle a}$ предел и этот предел равен частному значению ${\displaystyle f(a)}$ функции ${\displaystyle f(x)}$ в точке ${\displaystyle a}$: ${\displaystyle \lim _{x\to a}f(x)=f(a)}$.

Функция ${\displaystyle f(x)}$ называется непрерывной в точке ${\displaystyle a}$, если для любого ${\displaystyle \varepsilon >0}$ существует ${\displaystyle \delta >0}$ такое, что для всех значений аргумента ${\displaystyle x}$, удовлетворяющих условию ${\displaystyle |x-a|<\delta }$, справедливо неравенство ${\displaystyle |f(x)-f(a)|<\varepsilon }$.

Функция ${\displaystyle y=f(x)}$ называется непрерывной в точке ${\displaystyle a}$, если для любой сходящейся к ${\displaystyle a}$ последовательности значений аргумента ${\displaystyle x_{1},x_{2},...,x_{n}}$ соответствующая последовательность значений функции ${\displaystyle f(x_{1}),f(x_{2}),...,f(x_{n})}$ сходится к числу ${\displaystyle f(a)}$.

Из теоремы об эквивалентности определений предельного значения по Гейне и по Коши следует, что определения непрерывности функции по Гейне и по Коши эквивалентны^[2].

Пусть функция ${\displaystyle y=f(x)}$ определена в некоторой окрестности точки ${\displaystyle x_{0}}$. Считая ${\displaystyle x_{0}}$ исходной точкой, возьмём другое значение аргумента ${\displaystyle x=x_{0}+\Delta x}$, где величина ${\displaystyle \Delta x}$ — приращение аргумента. Величина изменения функции ${\displaystyle \Delta y=f(x_{0}+\Delta x)-f(x_{0})}$ — приращение функции ${\displaystyle f}$ в точке ${\displaystyle x_{0}}$, отвечающая приращению ${\displaystyle \Delta x}$ аргумента ${\displaystyle x}$.

Функция ${\displaystyle y=f(x)}$ называется непрерывной в точке ${\displaystyle x_{0}}$, если приращение ${\displaystyle \Delta y}$ функции в этой точке, отвечающее приращению ${\displaystyle \Delta x}$ аргумента, стремится к нулю при ${\displaystyle \Delta x\to 0}$: ${\displaystyle \lim _{\Delta x\to 0}\Delta y=0}$.

Все четыре определения непрерывности функции равносильны. В каждом конкретном случае пользуются тем определением, которое оказывается более удобным^[3].

Пусть область задания функции ${\displaystyle f\{x\}}$ включает точку ${\displaystyle a}$ и для любого ${\displaystyle \delta >0}$ найдётся хотя бы один элемент, лежащий на интервале ${\displaystyle [a;a+\delta )}$ (соответственно ${\displaystyle (a-\delta ;a]}$).

Функция ${\displaystyle f(x)}$ называется непрерывной в точке ${\displaystyle a}$ справа (слева), если правый (левый) предел этой функции в точке ${\displaystyle a}$ существует и равен частному значению ${\displaystyle f(a)}$ функции ${\displaystyle f(x)}$ в точке ${\displaystyle a}$: ${\displaystyle \lim _{x\to a+0}f(x)=f(a)}$ (слева${\displaystyle \lim _{x\to a-0}f(x)=f(a)}$).

Функция ${\displaystyle f(x)}$ называется непрерывной в точке ${\displaystyle a}$ справа (слева), если для любого ${\displaystyle \varepsilon >0}$ существует ${\displaystyle \delta >0}$ такое, что для всех значений аргумента ${\displaystyle x}$, удовлетворяющих условию ${\displaystyle a<x<a+\delta }$ (${\displaystyle a-\delta <x<a}$), справедливо неравенство ${\displaystyle |f(x)-f(a)|<\varepsilon }$.

Функция ${\displaystyle f(x)}$ называется непрерывной в точке ${\displaystyle a}$ справа (слева), если для любой сходящейся к ${\displaystyle a}$ последовательности значений аргумента ${\displaystyle f\{x_{n}\}}$, все элементы которой удовлетворяют условию ${\displaystyle x_{n}>a}$ (${\displaystyle x_{n}<a}$), соответствующая последовательность значений функции ${\displaystyle \{f(x_{n})\}}$ сходится к числу ${\displaystyle f(a)}$.

Эквивалентность определений по Гейне и по Коши вытекает из эквивалентности соответствующих определений предела функции.

Если функция ${\displaystyle f(x)}$ непрерывна в точке ${\displaystyle a}$ и слева, и справа, то она непрерывна в этой точке^[4].

Функция ${\displaystyle f(x)}$ непрерывна на множестве ${\displaystyle \{x\}}$, если она непрерывна в каждой точке этого множества.

Функция ${\displaystyle f(x)}$ непрерывна на отрезке ${\displaystyle [a,b]}$, если она непрерывна в каждой точке этого отрезка, и, кроме того, непрерывна справа в точке ${\displaystyle a}$ и слева в точке ${\displaystyle b}$.

Функция ${\displaystyle f}$ называется равномерно непрерывной на множестве ${\displaystyle E}$, если для любого ${\displaystyle \varepsilon >0}$ существует ${\displaystyle \delta >0}$ такое, что для любых двух точек ${\displaystyle x_{1}}$ и ${\displaystyle x_{2}}$ таких, что ${\displaystyle |x_{1}-x_{2}|<\delta }$, выполняется ${\displaystyle |f(x_{1})-f(x_{2})|<\varepsilon }$.

Функция ${\displaystyle f(x)}$ называется равномерно непрерывной на интервале ${\displaystyle (a,b)}$, если для всякого ${\displaystyle \varepsilon >0}$ существует такое ${\displaystyle \delta =\delta (\varepsilon )>0}$, что для любых точек ${\displaystyle x'}$ и ${\displaystyle x''}$ из интервала ${\displaystyle (a,b)}$, удовлетворяющих условию ${\displaystyle |x'-x''|<\delta }$ , верно неравенство ${\displaystyle |f(x')-f(x'')|<\varepsilon }$.

Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:

• функция ${\displaystyle f}$ называется полунепрерывной снизу в точке ${\displaystyle a}$, если для любого ${\displaystyle \varepsilon >0}$ существует такая окрестность ${\displaystyle U_{E}(a)}$, что ${\displaystyle f(x)>f(a)-\varepsilon }$ для всякого ${\displaystyle x\in U_{E}(a)}$;
• функция ${\displaystyle f}$ называется полунепрерывной сверху в точке ${\displaystyle a}$, если для любого ${\displaystyle \varepsilon >0}$ существует такая окрестность ${\displaystyle U_{E}(a)}$, что ${\displaystyle f(x)<f(a)+\varepsilon }$ для всякого ${\displaystyle x\in U_{E}(a)}$.

Между непрерывностью и полунепрерывностью имеется следующая связь:

• если взять функцию ${\displaystyle f}$, непрерывную в точке ${\displaystyle a}$, и уменьшить значение ${\displaystyle f(a)}$ (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке ${\displaystyle a}$;
• если взять функцию ${\displaystyle f}$, непрерывную в точке ${\displaystyle a}$, и увеличить значение ${\displaystyle f(a)}$ (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке ${\displaystyle a}$.

В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:

• если ${\displaystyle f(a)=-\infty }$, то будем считать такую функцию полунепрерывной снизу в точке ${\displaystyle a}$;
• если ${\displaystyle f(a)=+\infty }$, то будем считать такую функцию полунепрерывной сверху в точке ${\displaystyle a}$.

Пусть функция ${\displaystyle f(x)}$ определена в некоторой окрестности точки ${\displaystyle x_{0}}$. Согласно определению, непрерывность такой функции ${\displaystyle f(x)}$ в точке ${\displaystyle x_{0}}$ с использованием понятия односторонних пределов выражается соотношением: ${\displaystyle \lim _{x\to x_{0}-0}f(x)=\lim _{x\to x_{0}+0}f(x)=f(x_{0})}$^[5].

Если в точке ${\displaystyle x_{0}}$ функция ${\displaystyle f(x)}$ не является непрерывной, то говорят, что ${\displaystyle f(x)}$ разрывна в этой точке, и точку ${\displaystyle x_{0}}$называют точкой разрыва функции ${\displaystyle f(x)}$.

Точки разрыва функции классифицируются в зависимости от того, как именно нарушено условие её непрерывности: ${\displaystyle \lim _{x\to x_{0}-0}f(x)=\lim _{x\to x_{0}+0}f(x)=f(x_{0})}$.

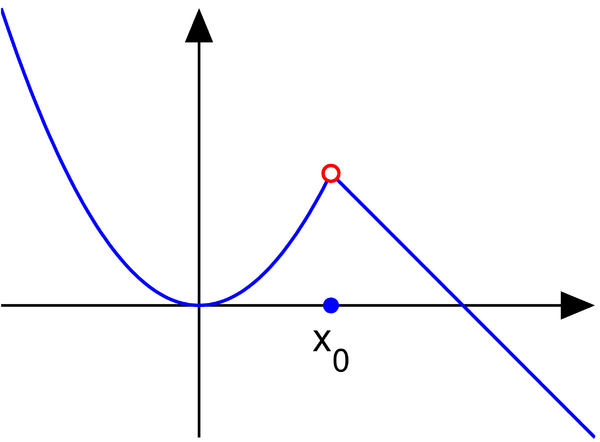
Если в точке ${\displaystyle x_{0}}$ функция ${\displaystyle f(x)}$ имеет предел слева и предел справа и они равны между собой, но не равны значению функции в точке ${\displaystyle x_{0}}$, то точка ${\displaystyle x_{0}}$ называется точкой устранимого разрыва функции ${\displaystyle f(x)}$: ${\displaystyle \lim _{x\to x_{0}-0}f(x)=\lim _{x\to x_{0}+0}f(x)\neq f(x_{0})}$.

Такое название оправдывается тем, что в этом случае достаточно изменить значение функции только в одной точке ${\displaystyle x_{0}}$, чтобы получить новую функцию, уже непрерывную в точке ${\displaystyle x_{0}}$. Если ${\displaystyle f(x)}$ имеет в точке ${\displaystyle x_{0}}$ устранимый разрыв, то функция ${\displaystyle F(x)={\begin{cases}f(x),&x\neq x_{0}\\\lim _{x\to x_{0}}f(x),&x=x_{0}\end{cases}}}$ непрерывна в точке ${\displaystyle x_{0}}$. Разрыв устранён с помощью изменения значения функции в точке ${\displaystyle x_{0}}$ (рис. 1).

Если ${\displaystyle \lim _{x\to x_{0}}f(x)}$ не существует, то точка ${\displaystyle x_{0}}$ называется точкой неустранимого paзрыва.

Если в точке ${\displaystyle x_{0}}$ функция ${\displaystyle f(x)}$ имеет конечные пределы слева и справа, но они разные${\displaystyle \lim \limits _{x\to x_{0}-0}f(x)\neq \lim \limits _{x\to x_{0}+0}f(x)}$, то точка ${\displaystyle x_{0}}$ называется точкой разрыва функции ${\displaystyle f(x)}$ с конечным скачком функции. 

При этом безразлично, совпадает или нет ${\displaystyle f(x_{0})}$ с одним из односторонних пределов (рис. 2).

Разрыв «полюс» возникает, если один из односторонних пределов бесконечен (рис. 3).

${\displaystyle \lim \limits _{x\to a-0}f(x)=\pm \infty }$ или ${\displaystyle \lim \limits _{x\to a+0}f(x)=\pm \infty }$.

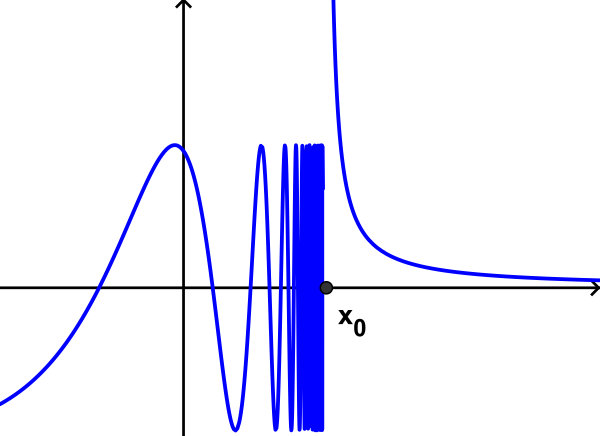
В точке существенного разрыва хотя бы один из односторонних пределов вообще отсутствует (рис. 4).

Точки устранимого разрыва и точки разрыва с конечным скачком функции называются точками разрыва первого рода. Каждая точка разрыва первого рода функции ${\displaystyle f(x)}$ характеризуется тем, что в этой точке функция ${\displaystyle f(x)}$ имеет конечный предел как слева, так и сnрава.

Все другие точки разрыва функции называются точками разрыва второго рода. Каждая точка разрыва второго рода функции ${\displaystyle f(x)}$ характеризуется тем, что в этой точке функция ${\displaystyle f(x)}$ не имеет конечного предела пo крайней мере с одной стороны — слева или справа^[6].

• если все значения ${\displaystyle x_{n}}$ последовательности ${\displaystyle \{x_{n}\}}$, стремящейся к числу ${\displaystyle \alpha }$, принадлежат ${\displaystyle [a,b]}$, то и ${\displaystyle \alpha \in [a,b]}$;
• если функция ${\displaystyle f}$ непрерывна на отрезке ${\displaystyle [a,b]}$, то она ограничена на нём;
• непрерывная на ${\displaystyle [a,b]}$ функция ${\displaystyle f}$ достигает в некоторых точках отрезка ${\displaystyle [a,b]}$ своих максимума и минимума, то есть существуют точки ${\displaystyle \alpha }$ и ${\displaystyle \beta }$, принадлежащие ${\displaystyle [a,b]}$, для которых имеют место равенства: ${\displaystyle \min _{x\in [a,b]}f(x)=f(\alpha )}$, ${\displaystyle \max _{x\in [a,b]}f(x)=f(\beta )}$. Таким образом, ${\displaystyle f(\alpha )\leqslant f(x)\leqslant f(\beta )}$ для всех ${\displaystyle x\in [a,b]}$;
• если функция ${\displaystyle f}$ непрерывна на отрезке ${\displaystyle [a,b]}$ и числа ${\displaystyle f(a)}$ и ${\displaystyle f(b)}$ не равны нулю и имеют разные знаки, то на интервале ${\displaystyle (a,b)}$ имеется по крайней мере одна точка ${\displaystyle c}$ такая, что ${\displaystyle f(c)=0}$;
• непрерывная на отрезке ${\displaystyle [a,b]}$ функция принимает все промежуточные значения между её значениями на концах отрезка ${\displaystyle [a,b]}$^[7].

К локальным свойствам относятся те свойства функции, которые справедливы в сколь угодно малой окрестности фиксированной точки области определения функции. Эти свойства характеризуют поведение функции при стремлении аргумента к исследуемой точке. Например, непрерывность функции в некоторой точке области её определения является локальным свойством этой функции.

К глобальным свойствам относятся свойства, связанные со всей областью определения функции^[8]:

• теорема о равномерной непрерывности: функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём;
• теорема Вейерштрасса о функции на компактном множестве: функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения;
• областью значений функции ${\displaystyle f}$, непрерывной на отрезке ${\displaystyle [a,b]}$, является отрезок ${\displaystyle [\min f,\ \max f],}$ где минимум и максимум берутся по отрезку ${\displaystyle [a,b]}$;
• теорема о промежуточном значении: если функция ${\displaystyle f}$ непрерывна на отрезке ${\displaystyle [a,b]}$ и число ${\displaystyle \varphi }$ удовлетворяет неравенству ${\displaystyle f(a)<\varphi <f(b)}$ или неравенству ${\displaystyle f(a)>\varphi >f(b),}$ то существует точка ${\displaystyle \xi \in (a,b),}$ в которой ${\displaystyle f(\xi )=\varphi }$;
• непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна;
• монотонная функция на отрезке ${\displaystyle [a,b]}$ непрерывна в том и только в том случае, когда область её значений является отрезком с концами ${\displaystyle f(a)}$ и ${\displaystyle f(b)}$;
• если функции ${\displaystyle f}$ и ${\displaystyle g}$ непрерывны на отрезке ${\displaystyle [a,b]}$, причём ${\displaystyle f(a)<g(a)}$ и ${\displaystyle f(b)>g(b),}$ то существует точка ${\displaystyle \xi \in (a,b),}$ в которой ${\displaystyle f(\xi )=g(\xi ).}$ Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.

Арифметические операции над непрерывными функциями приводят снова к непрерывным функциям^[9].

Теорема. Пусть на одном и том же множестве заданы функции ${\displaystyle f(x)}$ и ${\displaystyle {\text{g}}(x)}$, непрерывные в точке ${\displaystyle a}$. Тогда их сумма ${\displaystyle f(x)+{\text{g}}(x)}$, разность ${\displaystyle f(x)-{\text{g}}(x)}$, произведение ${\displaystyle f(x)\cdot {\text{g}}(x)}$, а также частное ${\displaystyle f(x) \over {{\text{g}}(x)}}$ (при дополнительном условии ${\displaystyle {\text{g}}(a)\neq 0}$) непрерывны в точке ${\displaystyle a}$.

Функции, полученные в результате суперпозиции двух или нескольких функций, называют сложными. Под суперпозицией двух функций понимают функцию, полученную в результате наложения или последовательного применения указанных двух функций в определённом порядке^[9].

Теорема. Пусть функция ${\displaystyle x=\varphi (t)}$ непрерывна в точке ${\displaystyle a}$, а функция ${\displaystyle y=f(x)}$ непрерывна в точке ${\displaystyle b=\varphi (a)}$. Тогда сложная функция ${\displaystyle y=f[\varphi (t)]=F(t)}$ непрерывна в точке ${\displaystyle a}$.

Теорема. Если функция ${\displaystyle u=\varphi (x)}$ в точке ${\displaystyle x_{0}}$ имеет предел, равный числу ${\displaystyle A}$, а функция ${\displaystyle y=f(u)}$ непрерывна в точке ${\displaystyle u=A}$, то сложная функция ${\displaystyle y=f[\varphi (x)]}$ в точке ${\displaystyle x_{0}}$ имеет предел, равный ${\displaystyle f(A)}$: ${\displaystyle \lim _{x\to x_{0}}f[\varphi (x)]=f\lim _{x\to x_{0}}[\varphi (x)]}$.

Это соотношение выражает правило перехода к пределу под знаком непрерывной функции^[10].

Если функция ${\displaystyle f(x)}$ непрерывна в точке ${\displaystyle x_{0}}$ и ${\displaystyle f(x_{0})\neq 0}$, то существует окрестность ${\displaystyle (x_{0}-\delta ,x_{0}+\delta )}$ точки ${\displaystyle x_{0}}$, в которой функция ${\displaystyle f(x)}$ не обращается в нуль и сохраняет один и тот же знак (знак числа${\displaystyle f(x_{0})}$)^[11].

Если функция ${\displaystyle y=f(x)}$ дифференцируема в данной точке ${\displaystyle x}$, то она непрерывна в этой точке. Обратное заключение неверно: из непрерывности функции ${\displaystyle f(x)}$ в некоторой точке ${\displaystyle x}$ не следует дифференцируемость функции в этой точке^[12].

Функции, которые получаются из основных с помощью конечного числа арифметических операций, а также операций взятия функции от функции, применённых конечное число раз, называются элементарными функциями. Все основные элементарные функции непрерывны в каждой точке своих областей определения^[13].

Функция ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,}$ задаваемая формулой

${\displaystyle f(x)={\begin{cases}{\frac {\sin x}{x}},&x\neq 0\\0,&x=0\end{cases}}}$,

непрерывна в любой точке ${\displaystyle x\neq 0.}$ Точка ${\displaystyle x=0}$ является точкой устранимого разрыва, ибо предел функции

${\displaystyle \lim \limits _{x\to 0}f(x)=\lim \limits _{x\to 0}{\frac {\sin x}{x}}=1\neq f(0).}$

Функция

${\displaystyle f(x)=\operatorname {sgn} x={\begin{cases}-1,&x<0\\0,&x=0\\1,&x>0\end{cases}},\quad x\in \mathbb {R} }$

называется функцией знака.

Эта функция непрерывна в каждой точке ${\displaystyle x\neq 0}$.

Точка ${\displaystyle x=0}$ является точкой разрыва первого рода, причём

${\displaystyle \lim \limits _{x\to 0-}f(x)=-1\neq 1=\lim \limits _{x\to 0+}f(x)}$,

в то время как в самой точке функция обращается в нуль.

Функция Хевисайда, определяемая как

${\displaystyle f(x)={\begin{cases}1,&x\geqslant 0\\0,&x<0\end{cases}},\quad x\in \mathbb {R} }$,

является всюду непрерывной, кроме точки ${\displaystyle x=0}$, где функция терпит разрыв первого рода. Тем не менее в точке ${\displaystyle x=0}$ существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.

Аналогично, ступенчатая функция, определяемая как

${\displaystyle f(x)={\begin{cases}1,&x>0\\0,&x\leqslant 0\end{cases}},\quad x\in \mathbb {R} }$,

является примером непрерывной слева функции на всей области определения.

Функция

${\displaystyle f(x)={\begin{cases}1,&x\in \mathbb {Q} \\0,&x\in \mathbb {R} \setminus \mathbb {Q} \end{cases}}}$

называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция разрывна в каждой точке, поскольку в сколь угодно малой окрестности любой точки имеются как рациональные, так и иррациональные числа.

Функция

${\displaystyle f(x)={\begin{cases}{\frac {1}{n}},&x={\frac {m}{n}}\in \mathbb {Q} ,\ {\text{НОД}}(m,n)=1\\0,&x\in \mathbb {R} \setminus \mathbb {Q} \end{cases}}}$

называется функцией Римана, или «функцией Тома».

Эта функция непрерывна на множестве иррациональных чисел (${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$), поскольку предел функции в каждой иррациональной точке равен нулю (если последовательность ${\displaystyle x_{k}=m_{k}/n_{k}\to x\notin \mathbb {Q} }$, то с необходимостью ${\displaystyle n_{k}\to \infty }$). Во всех же рациональных точках она разрывна.