Икосаэдр

Перейти к материалам ОГЭ/ЕГЭ

РУВИКИ для ОГЭ/ЕГЭ

        Переходите на портал РУВИКИ, где собраны материалы для подготовки к ОГЭ и ЕГЭ

Перейти

Выпуклый правильный икосаэдр

Деталь памятника Спинозе в Амстердаме

Икосаэдр (от др.-греч. εἴκοσι — двадцать и ἕδρα — площадка^[1]) — это многогранник с 20 гранями.

Существует бесконечно много непохожих икосаэдров, некоторые из которых имеют больше симметрий, другие меньше. Наиболее известен (выпуклый, незвёздчатый) правильный икосаэдр — один из правильных многогранников, гранями которого являются 20 правильных треугольников.

Правильный икосаэдр

Два вида правильных икосаэдров
Выпуклый правильный икосаэдр	Большой икосаэдр

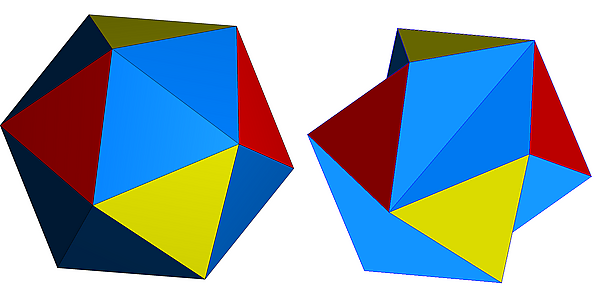
Имеется два тела, одно выпуклое и одно невыпуклое, оба из которых называются правильными икосаэдрами. Оба имеют 30 рёбер и 20 граней в виде правильных треугольников, которые сходятся по 5 в каждой из его 12 вершин. Оба имеют икосаэдральную симметрию. Термин «правильный икосаэдр» обычно относится к выпуклому виду, а невыпуклая форма называется большим икосаэдром.

Выпуклый правильный икосаэдр[править | править код]

Под выпуклым правильным икосаэдром обычно понимается правильный икосаэдр, один из пяти правильных многогранников, и он представлен символом Шлефли {3, 5}. Многогранник имеет 20 треугольных граней по 5 граней в каждой вершине.

Его двойственным многогранником является правильный додекаэдр {5, 3}, имеющий три правильных пятиугольных грани вокруг каждой вершины.

Большой икосаэдр[править | править код]

Большой икосаэдр является одним из четырёх звёздчатых тел Кеплера — Пуансо. Его Символ Шлефли равен ${\textstyle \left\{3,{\frac {5}{2}}\right\}}$ . Подобно выпуклому виду он имеет также 20 граней в виде правильных треугольников, но его вершинной фигурой служит пентаграмма, а не пятиугольник, что приводит к геометрически пересекающимся граням. Пересечения треугольников не представляют новых рёбер.

Его двойственным многогранником является большой звёздчатый додекаэдр ${\textstyle \left\{{\frac {5}{2}},3\right\}}$ , имеющий три правильных звёздчатых пятиугольных грани вокруг каждой вершины.

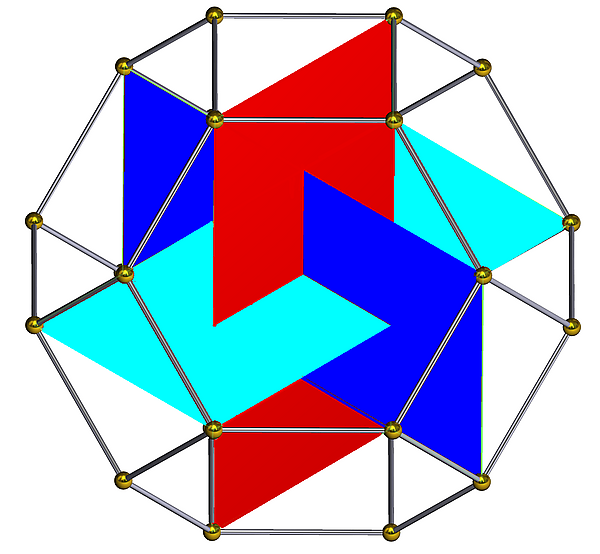
Звёздчатые формы икосаэдра

Образование звёздчатой формы — это процесс расширения граней или рёбер многогранника, пока они не соприкоснутся с образованием нового многогранника. Это осуществляется симметрично так, что результирующее тело сохраняет все симметрии родительского тела.

В книге «Пятьдесят девять икосаэдров» (The Fifty-Nine Icosahedra) Коксетера с соавторами перечислено 58 таких звёздчатых форм правильного икосаэдра.

Из них многие имеют отдельную грань в каждой из 20 плоскостей, а потому являются также икосаэдрами. Большой икосаэдр среди них.

Другие звёздчатые формы имеют более одной грани на каждой плоскости или формируются как соединение более простых многогранников. Они не являются, строго говоря, икосаэдрами, хотя и упоминаются часто как таковые.

Пиритоэдральная симметрия

Пиритоэдральная и тетраэдральная симметрии

Диаграммы Коксетера

(пираэдральная)

(тетраэдральный)

Символ Шлефли

s{3,4}
sr{3,3} или

s{\begin{Bmatrix}3\\3\end{Bmatrix}}

Грани

20 треугольников:
8 правильных
12 равнобедренных

Рёбра

30 (6 коротких + 24 длинных)

Вершины

12

Группа симметрии

T_h, [4,3⁺], (3*2), порядок 24

Группы вращений

T_d, [3,3]⁺, (332), порядок 12

Двойственный многогранник

пиритоэдр

Свойства

выпуклый

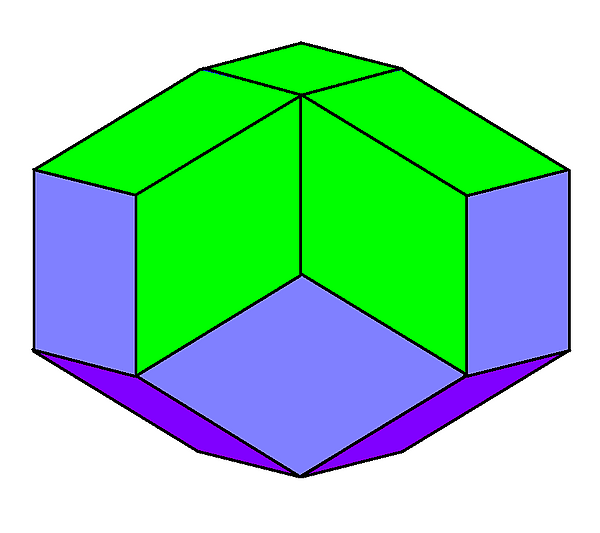
Развёртка


Правильный икосаэдр топологически идентичен кубооктаэдру с 6 квадратными гранями, разбитыми по диагоналям.

Правильный икосаэдр может быть искривлён или размечен так, что он будет обладать более низкой пироэдральной симметрией^[2] и он называется плосконосым октаэдром, плосконосым тетратетраэдом, плосконосым тетраэдром и псевдоикосаэдром. Его можно рассматривать как альтернированный усечённый октаэдр. Если все треугольники правильные, симметрии можно различить путём раскраски 8 и 12 наборов треугольников различным образом.

Пиритоэдральная симметрия имеет символ (3*2), [3⁺,4] и порядок 24. Тетраэдральная симметрия имеет символ (332), [3,3]⁺ и порядок 12. Эти низкие симметрии позволяют искривление из 20 равносторонних треугольных граней, получая 8 правильных треугольников и 12 конгруэнтных равнобедренных треугольников.

Эти симметрии дают диаграммы Коксетера: и соответственно, и оба обладают более низкой симметрией, чем симметрии , (*532), [5,3] порядка 120 правильного икосаэдра.

Декартовы координаты[править | править код]

Построение из вершин усечённого октаэдра, показаны внутренние прямоугольники.

Координаты 12 вершин могут быть заданы векторами, определёнными всеми положительными циклическими перестановками и изменениям знака координат вида (2, 1, 0). Эти координаты представляют усечённый октаэдр с альтернированным удалением вершин.

Это построение называется плосконосым тетраэдром, если образовано из вектора (ϕ, 1, 0), где ϕ является золотым сечением^[2].

Икосаэдр Йессена[править | править код]

Правильный икосаэдр и икосаэдр Йессена.

В икосаэдре Йессена, который иногда называют ортогональным икосаэдром Йессена, 12 равнобедренных граней расположены иначе, так что образуют невыпуклое тело. Он имеет прямые двугранные углы.

Он равносоставлен с кубом, что значит, что его можно разрезать на более мелкие многогранники, из которых можно составить полный куб.

Другие икосаэдры

Ромбоикосаэдр

Ромбоикосаэдр[править | править код]

Ромбоикосаэдр является зоноэдром, состоящим из 20 равных ромбов. Он может быть получен из ромботриаконтаэдра путём удаления 10 средних граней. Хотя все грани конгруэнтны, ромбоикосаэдр не гране транзитивен.

Симметрии пирамиды и призмы[править | править код]

Общие симметрии икосаэдра с пирамидами и призмами:

19-угольная пирамида (плюс 1 основание = 20).
18-угольная призма (плюс 2 основания = 20).
9-угольная антипризма (2 набора по 9 сторон + 2 основания = 20).
10-угольная бипирамида (2 набора по 10 сторон = 20).
10-угольный трапецоэдр (2 набора по 10 сторон = 20).

Правильногранные многогранники[править | править код]

Некоторые правильногранные многогранники являются икосаэдрами^[3]: даны обозначения Джонсона и Залгаллера

J₂₂ (М₄+А₆)	J₃₅ (М₄+П₆+М₄)	J₃₆ (М₄+П₆+М₄)	J₅₉ (М₃+М₁₅+М₃)	J₆₀ (М₁₅+2М₃)	J₉₂ (М₂₀)
Скрученно удлинённый трёхскатный купол	Удлинённый трёхскатный прямой бикупол	Удлинённый трёхскатный повёрнутый бикупол	Дважды противоположно наращённый додекаэдр	Дважды косо наращённый додекаэдр	Уплощённая треугольная клиноротонда

16 треугольников 3 квадрата 1 шестиугольник	8 треугольников 12 квадратов	8 треугольников 12 квадратов	10 треугольников 10 пятиугольников	10 треугольников 10 пятиугольников	13 треугольников 3 квадрата 3 пятиугольника 1 шестиугольник

См. также

Ромботриаконтаэдр

Примечания

↑ Jones, 2003.
↑ ¹ ² John Baez. Fool's Gold (неопр.) (11 сентября 2011). Дата обращения: 5 августа 2019. Архивировано 19 мая 2018 года.
↑ Icosahedron Архивная копия от 8 декабря 2020 на Wayback Machine on Mathworld.

Литература

Daniel Jones. English Pronouncing Dictionary / Peter Roach, James Hartmann, Jane Setter. — Cambridge: Cambridge University Press, 2003. — ISBN 3-12-539683-2.

[_2a759426f3139d59-1] Jones, 2003.

[Baez-2] ¹ ² John Baez. Fool's Gold (неопр.) (11 сентября 2011). Дата обращения: 5 августа 2019. Архивировано 19 мая 2018 года.

[MW-3] Icosahedron Архивная копия от 8 декабря 2020 на Wayback Machine on Mathworld.

[1]

[2]

[3]