Линейная операция

Лине́йная опера́ция над векторами — операция сложения векторов либо операция умножения вектора на число^[1]^[2]^[3]^[4]. Иногда к этим двум операциям добавляют операцию вычитания векторов^[5].

Линейные операции над векторами — операции сложения векторов, вычитания векторов и умножения вектора на скаляр. Эти операции называются линейными потому, что если над векторами $\mathbf {a}$ , $\mathbf {b}$ , $\mathbf {c}$ и $\mathbf {d}$ выполнить конечное количество произвольных действий сложения, вычитания и умножения на скаляр, то в результате получится новый вектор — линейная комбинация исходных векторов

\alpha \mathbf {a} +\beta \mathbf {b} +\gamma \mathbf {c} +\delta \mathbf {d}

,

где $\alpha ,\beta ,\gamma ,\delta$ — скаляры (действительные числа)^[5].

Сложе́ние векторо́в, или геометри́ческое сложе́ние векторо́в^[6] (англ. addition of vectors) — операция, ставящая в соответствие двум векторам третий вектор — сумму векторов^[7]. При этом сумма $\mathbf {a} +\mathbf {b}$ двух векторов $\mathbf {a}$ и $\mathbf {b}$ — это третий вектор $\mathbf {c} =\mathbf {a} +\mathbf {b}$ , проведённый из начала одного вектора к концу второго, причём конец первого вектора совпадает с началом второго (правило треугольника). Сумма векторов геометрически строится с помощью правил — алгоритмов построения вектора суммы по векторам-слагаемым (см. рисунок с треугольником сложения векторов справа)^[8]^[9]^[6]^[10].

Три вектора $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c} =\mathbf {a} +\mathbf {b}$ всегда компланарны, то есть параллельны одной плоскости^[11].

Векторы, которые складываются, называются слагаемыми векторами, а результат сложения — геометрической суммой, или результирующим вектором^[12].

Результат сложения векторов не зависит от расположения первого слагаемого, при его изменении треугольник сложения будет параллельно перенесён^[9].

Существуют два действия, обратных сложению векторов^[13]:

Законы сложения

Операция сложения в математике в векторной алгебре векторов как геометрическое построение по правилу многоугольника возникла как обобщение операции вычисления равнодействующей силы в механике. Правомерность названия «сложение» заключается также и в том, что операция сложения векторов подчиняется тем же двум законам, что и арифметическая операция сложения чисел, а именно^[14]:

Эти законы и аналогичные законы для сложения чисел записываются одинаково. Что не только важно, но и удобно, поскольку позволяет работать с векторными равенствами, не переучиваясь, так же, как с числовыми равенствами. Эта аналогия распространяется и на вычитание векторов, а также действия с равенствами векторов^[15].

Вычита́ние векторо́в, или геометри́ческое вычита́ние векторо́в (англ. subtraction of vectors) — операция, обратная сложению, ставящая в соответствие двум векторам третий вектор — разность векторов, другими словами, по сумме векторов и одному слагаемому определяется второе слагаемое^[16]^[17]^[18]^[19]^[20]. При этом разность $\mathbf {a} -\mathbf {b}$ двух векторов $\mathbf {a}$ и $\mathbf {b}$ — это третий вектор $\mathbf {c} =\mathbf {a} -\mathbf {b}$ такой, что $\mathbf {c} +\mathbf {b} =\mathbf {a}$ (см. рисунок справа с треугольником вычитания векторов)^[21]^[22]^[23]^[24]^[20]. Первый вектор разности называется уменьшаемым, а второй — вычитаемым^[25]^[18]^[19]^[20].

Умноже́ние ве́ктора на число́ (англ. scalar multiplication of a vector) — операция, ставящая в соответствие вектору и числу другой коллинеарный вектор — произведение вектора на это число^[26]. При этом произведение вектора и числа в случае ненулевых вектора и числа — новый вектор, у которого^[27]^[23]:

модуль равен произведению модуля исходного вектора на абсолютную величину числа;
направление, совпадающее с направлением исходного вектора, если число положительно, и противоположное, если число отрицательно (см. рисунок справа).

Обозначение произведения вектора $\mathbf {a}$ и скаляра $\lambda$ следующее^[27]^[23]:

\mathbf {a} \lambda

или

\lambda \mathbf {a} .

В итоге получаем^[27]:

|\lambda \mathbf {a} |=|\mathbf {a} \lambda |=|\lambda ||\mathbf {a} |.

Произведение вектора и числа равно нулевому вектору тогда и только тогда, когда хотя бы один из сомножителей равен нулю^[27]^[23]:

\lambda \mathbf {0} =0\mathbf {a} =\mathbf {0} .

Существуют два действия, обратных умножению вектора на число:

Законы умножения на скаляр

Три закона умножения вектора на скаляр те же самые, что и законы умножения чисел^[27]:

переместительности (коммутативность):

\lambda \mathbf {a} =\mathbf {a} \lambda

;

сочетательности (ассоциативность):

\lambda (\mu \mathbf {a} )=(\lambda \mu )\mathbf {a}

;

распределительности (дистрибутивность):

(\mathbf {a} +\mathbf {b} )\lambda =\mathbf {a} \lambda +\mathbf {b} \lambda

;

(\lambda +\mu )\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {a}

.

Разложение вектора

Геометрическое вычитание векторов — операция, обратная геометрическому сложению векторов. Кроме неё, обратной операцией к сложению векторов является геометрическое разложение вектора, или просто разложение вектора — операция представления данного вектора в виде замыкающей нескольких векторов. Геометрически строится ломаная линия, которую замыкает данный вектор. Но так эту операцию определить нельзя, и чтобы её определить, нужно наложить на геометрические слагаемые определённые условия^[13].

Применение линейных операций — использование линейных операций над векторами:

для решения математических и физических задач.

Коллинеарность и компланарность точек

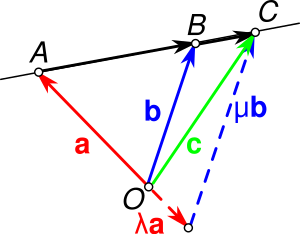
Задача 1. Три точки $A$ , $B$ и $C$ , где

{\overrightarrow {OA}}=\mathbf {a}

,

{\overrightarrow {OB}}=\mathbf {b}

,

{\overrightarrow {OC}}=\mathbf {c}

,

\mathbf {c} =\lambda \mathbf {a} +\mu \mathbf {b}

,

тогда и только тогда коллинеарны, то есть лежат на одной прямой, когда (см. рисунок справа)

\lambda +\mu =1

.

Исключение: коллинеарность векторов $\mathbf {a}$ и $\mathbf {b}$ , когда три точки $A$ , $B$ и $C$ всегда лежат на одной прямой при любых числах $\lambda$ и $\mu$ ^[28].

Решение^[29]

1. Необходимость. Пусть три точки $A$ , $B$ и $C$ лежат на одной прямой (см. рисунок справа вверху). Тогда векторы ${\overrightarrow {AB}}=\mathbf {b} -\mathbf {a}$ и ${\overrightarrow {AC}}=\mathbf {c} -\mathbf {a}$ коллинеарны, то есть

\mathbf {c} -\mathbf {a} =\mu (\mathbf {b} -\mathbf {a} )

,

следовательно,

\mathbf {c} =\mathbf {a} +\mu (\mathbf {b} -\mathbf {a} )=(1-\mu )\mathbf {a} +\mu \mathbf {b}

,

но разложение вектора $\mathbf {c}$ по векторам $\mathbf {a}$ и $\mathbf {b}$ единственно при их неколлинеарности, поэтому окончательно получаем^[28]:

\lambda =1-\mu

,

\quad \lambda +\mu =1

.

2. Достаточность. Обратно, пусть $\lambda +\mu =1$ , тогда

\mathbf {c} -\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {b} -\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {b} -(\lambda +\mu )\mathbf {a} =\mu (\mathbf {b} -\mathbf {a} )

,

поэтому векторы ${\overrightarrow {AC}}=\mathbf {c} -\mathbf {a}$ и ${\overrightarrow {AB}}=\mathbf {b} -\mathbf {a}$ коллинеарны и отложены от одной и той же точки $A$ , следовательно, три точки $A$ , $B$ и $C$ лежат на одной прямой^[29].

Замечание. Уравнение $\mathbf {c} =\lambda \mathbf {a} +\mu \mathbf {b}$ с ограничением $\lambda +\mu =1$ — относительно полюса $O$ векторное уравнение прямой, которая проходит через две заданные точки $A$ и $B$ , $\mathbf {a} ={\overrightarrow {OA}}$ , $\mathbf {b} ={\overrightarrow {OB}}$ , $\mathbf {c} ={\overrightarrow {OC}}$ . При этом значения коэффициентов $\lambda$ и $\mu$ вычисляются как частные векторов^[30]:

\lambda ={\frac {\overrightarrow {BC}}{\overrightarrow {BA}}};

\quad \mu ={\frac {\overrightarrow {AC}}{\overrightarrow {AB}}}.

Используя полученные результаты, найдем такой радиус-вектор ${\overrightarrow {OC}}=\mathbf {c}$ , который делит отрезок $AB$ в отношении ${\frac {x}{y}}$ . Итак, имеем, учитывая, что в данном случае коэффициенты $\lambda ,\mu \geqslant 0$ ^[30]:

{\frac {AC}{CB}}={\frac {x}{y}}

,

{\frac {AC}{AB}}={\frac {AC}{AC+CB}}={\frac {x}{x+y}}=\mu

,

\lambda =1-\mu ={\frac {y}{x+y}}

,

\mathbf {c} =\lambda \mathbf {a} +\mu \mathbf {b} ={\frac {y\mathbf {a} +x\mathbf {b} }{x+y}}

.

Задача 2. Четыре точки $A$ , $B$ , $C$ и $D$ , где

{\overrightarrow {OA}}=\mathbf {a}

,

{\overrightarrow {OB}}=\mathbf {b}

,

{\overrightarrow {OC}}=\mathbf {c}

,

{\overrightarrow {OD}}=\mathbf {d}

,

\mathbf {d} =\lambda \mathbf {a} +\mu \mathbf {b} +\mu \mathbf {c}

,

тогда и только тогда компланарны, то есть лежат в одной плоскости, когда (см. рисунок справа)

\lambda +\mu +\nu =1

.

Исключение: компланарность векторов $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ , когда четыре точки $A$ , $B$ , $C$ и $D$ всегда лежат в одной плоскости при любых числах $\lambda$ , $\mu$ и $\nu$ ^[30].

Решение^[31]

1. Необходимость. Пусть четыре точки $A$ , $B$ , $C$ и $D$ лежат в одной плоскости. Тогда векторы ${\overrightarrow {AB}}=\mathbf {b} -\mathbf {a}$ , ${\overrightarrow {AC}}=\mathbf {c} -\mathbf {a}$ и ${\overrightarrow {AF}}=\mathbf {d} -\mathbf {a}$ компланарны, то есть

\mathbf {d} -\mathbf {a} =\mu (\mathbf {b} -\mathbf {a} )+\nu (\mathbf {c} -\mathbf {a} )

,

следовательно,

\mathbf {d} =\mathbf {a} +\mu (\mathbf {b} -\mathbf {a} )+\nu (\mathbf {c} -\mathbf {a} )=(1-\mu -\nu )\mathbf {a} +\mu \mathbf {b} +\nu \mathbf {c}

,

но разложение вектора $\mathbf {d}$ по векторам $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ единственно при их некомпланарности, поэтому окончательно получаем^[31]:

\lambda =1-\mu -\nu

,

\quad \lambda +\mu +\nu =1

.

2. Достаточность. Обратно, пусть $\lambda +\mu +\nu =1$ , тогда

\mathbf {d} -\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {b} +\nu \mathbf {c} -\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {b} +\nu \mathbf {c} -(\lambda +\mu +\nu )\mathbf {a} =\mu (\mathbf {b} -\mathbf {a} )+\nu (\mathbf {c} -\mathbf {a} )

,

поэтому векторы ${\overrightarrow {AD}}=\mathbf {d} -\mathbf {a}$ , ${\overrightarrow {AB}}=\mathbf {b} -\mathbf {a}$ и ${\overrightarrow {AC}}=\mathbf {c} -\mathbf {a}$ компланарны и отложены от одной и той же точки $A$ , следовательно, четыре точки $A$ , $B$ , $C$ и $D$ лежат в одной плоскости^[32].

Замечание. Уравнение $\mathbf {d} =\lambda \mathbf {a} +\mu \mathbf {b} +\mu \mathbf {c}$ с ограничением $\lambda +\mu +\nu =1$ — относительно полюса $O$ векторное уравнение плоскости, которая проходит через три заданные точки $A$ , $B$ и $C$ , $\mathbf {a} ={\overrightarrow {OA}}$ , $\mathbf {b} ={\overrightarrow {OB}}$ , $\mathbf {c} ={\overrightarrow {OC}}$ , $\mathbf {d} ={\overrightarrow {OD}}$ ^[32].

Построение треугольника

Здесь приведены две задачи на построение треугольника.

Задача 3. Найти условие, которому отвечают три вектора, образующие треугольник (см. рисунок справа)^[33].

Решение. Рисунок справа показывает, что искомое условие для трёх векторов следующее:

\mathbf {a} +\mathbf {b} +\mathbf {c} =0

,

потому что тогда и только тогда ломаная линия $BCAB$ будет замкнута и получится треугольник^[33].

Задача 4. Доказать, что всегда можно построить треугольник с тремя сторонами, равными и параллельными трём медианам данного треугольника $ABC$ (см. рисунок справа)^[33].

Решение. Пусть $A'$ , $B'$ и $C'$ — середины сторон треугольника соответственно $BC$ , $CA$ и $AB$ . Разложим векторы ${\overrightarrow {AA'}}$ , ${\overrightarrow {BB'}}$ и ${\overrightarrow {CC'}}$ , которые представляют медианы треугольника, по векторам $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ . Разложим медиану ${\overrightarrow {AA'}}$ :

{\overrightarrow {BA'}}={\frac {1}{2}}{\overrightarrow {BC}}={\frac {1}{2}}\mathbf {a}

,

{\overrightarrow {AA'}}={\overrightarrow {AB}}+{\overrightarrow {BA'}}=\mathbf {c} +{\frac {1}{2}}\mathbf {a}

,

аналогично

{\overrightarrow {BB'}}=\mathbf {a} +{\frac {1}{2}}\mathbf {b}

,

{\overrightarrow {CC'}}=\mathbf {b} +{\frac {1}{2}}\mathbf {c}

,

и проверяем условие того, что векторы ${\overrightarrow {AA'}}$ , ${\overrightarrow {BB'}}$ и ${\overrightarrow {CC'}}$ составляют треугольник — условие задачи 3^[34]:

\mathbf {a} +\mathbf {b} +\mathbf {c} =0

,

{\overrightarrow {AA'}}+{\overrightarrow {BB'}}+{\overrightarrow {CC'}}=\mathbf {c} +{\frac {1}{2}}\mathbf {a} +\mathbf {a} +{\frac {1}{2}}\mathbf {b} +\mathbf {b} +{\frac {1}{2}}\mathbf {c} ={\frac {3}{2}}(\mathbf {a} +\mathbf {b} +\mathbf {c} )=0

.

Середина отрезка

Задача 5. По двум радиус-векторам ${\overrightarrow {OA}}=\mathbf {a}$ и ${\overrightarrow {OB}}=\mathbf {b}$ концов $A$ и $B$ отрезка $AB$ найти радиус-вектор ${\overrightarrow {OC}}=\mathbf {c}$ середины $C$ этого отрезка^[34].

Решение. Вычислим искомый радиус-вектор:

\mathbf {c} ={\overrightarrow {OC}}={\overrightarrow {OA}}+{\overrightarrow {AC}}={\overrightarrow {OA}}+{\frac {1}{2}}{\overrightarrow {AB}}=\mathbf {a} +{\frac {1}{2}}(\mathbf {b} -\mathbf {a} )={\frac {1}{2}}(\mathbf {a} +\mathbf {b} ).

Задача 6. Доказать, что если две диагонали произвольного четырёхугольника делят друг друга пополам, то такой четырёхугольник — параллелограмм^[34].

Решение. Пусть $\mathbf {a}$ , $\mathbf {b}$ , $\mathbf {c}$ и $\mathbf {d}$ — радиус-векторы четырёх последовательных вершин четырёхугольника $ABCD$ . Тогда

\mathbf {e'} ={\frac {1}{2}}(\mathbf {a} +\mathbf {c} )

—

радиус-вектор середины одной диагонали, а

\mathbf {e''} ={\frac {1}{2}}(\mathbf {b} +\mathbf {d} )

—

радиус-вектор середины другой диагонали. Поскольку диагонали делят друг друга пополам, то их середины совпадают:

{\frac {1}{2}}(\mathbf {a} +\mathbf {c} )={\frac {1}{2}}(\mathbf {b} +\mathbf {d} )

,

\mathbf {b} -\mathbf {a} =\mathbf {c} -\mathbf {d}

,

другими словами, вектор $\mathbf {b} -\mathbf {a}$ равен и параллелен вектору $\mathbf {c} -\mathbf {d}$ . Поскольку эти векторы представляют противоположные стороны четырёхугольника $ABCD$ , то $ABCD$ — параллелограмм^[35].

Пересечение трёх прямых в одной точке

Задача 7. Доказать, что медианы произвольного треугольника пересекаются в одной точке и найти радиус-вектор этой точки^[32].

Решение^[36]

Пусть вершины произвольного треугольника $A$ , $B$ и $C$ имеют радиус-векторы соответственно $\mathbf {r} _{1}={\overrightarrow {OA}}$ , $\mathbf {r} _{2}={\overrightarrow {OB}}$ и $\mathbf {r} _{3}={\overrightarrow {OC}}$ . Обозначим через $A'$ , $B'$ и $C'$ середины сторон соответственно $BC$ , $CA$ и $AB$ (см. рисунок к задаче 4). Тогда, по задаче 5, радиус-вектор

\mathbf {r} '={\overrightarrow {OA'}}={\frac {1}{2}}(\mathbf {r} _{2}+\mathbf {r} _{2}),

следовательно, по задаче задаче 1, уравнение прямой, проходящей серз две точки $A$ и $A'$ , то есть уравнение медианы $AA'$ ,

\mathbf {r} =\lambda \mathbf {r} _{1}+(1-\lambda ){\frac {1}{2}}(\mathbf {r} _{1}+\mathbf {r} _{3})=\lambda \mathbf {r} _{1}+{\frac {1-\lambda }{2}}(\mathbf {r} _{2}+\mathbf {r} _{3}),

где $\mathbf {r}$ — произвольный радиус-вектор. Аналогично уравнение медианы $BB'$ следующее^[32]:

\mathbf {r} =\mu \mathbf {r} _{2}+{\frac {1-\mu }{2}}(\mathbf {r} _{3}+\mathbf {r} _{1}).

Приравняем оба выражения и получим уравнение точки пересечения медиан $AA'$ и $BB'$ ^[32]:

\lambda \mathbf {r} _{1}+{\frac {1-\lambda }{2}}(\mathbf {r} _{2}+\mathbf {r} _{3})=\mu \mathbf {r} _{2}+{\frac {1-\mu }{2}}(\mathbf {r} _{3}+\mathbf {r} _{1}).

Теперь приравняем коэффициенты при $\mathbf {r} _{1}$ , $\mathbf {r} _{2}$ и $\mathbf {r} _{3}$ ^[32]:

\lambda ={\frac {1-\mu }{2}},\quad \mu ={\frac {1-\lambda }{2}},\quad {\frac {1-\lambda }{2}}={\frac {1-\mu }{2}},

откуда

\lambda =\mu ={\frac {1}{3}},

и уравнение точки пересечения медиан $AA'$ и $BB'$

\mathbf {r} =\lambda \mathbf {r} _{1}+{\frac {1-\lambda }{2}}(\mathbf {r} _{2}+\mathbf {r} _{3})={\frac {1}{3}}(\mathbf {r} _{1}+\mathbf {r} _{2}+\mathbf {r} _{3}).

При определении точки пересечения медиан $BB'$ и $CC'$ будет получен тот же результат по причине симметрии полученного выражения, поэтому третья медиана проходит через ту же точку^[37].

Задача 8. Доказать, что биссектрисы произвольного треугольника пересекаются в одной точке и найти радиус-вектор этой точки^[38].

Решение^[38]

Треугольник из векторов и биссектрисы

Пусть биссектрисы $AA'$ и $BB'$ треугольника $ABC$ пересекаются в точке $P$ (см. рисунок справа), и пусть

\mathbf {a} _{1}={\frac {\mathbf {a} }{|\mathbf {a} |}},\quad \mathbf {b} _{1}={\frac {\mathbf {b} }{|\mathbf {b} |}},\quad \mathbf {c} _{1}={\frac {\mathbf {c} }{|\mathbf {c} |}}

—

орты векторов

\mathbf {a} ={\overrightarrow {BC}},\quad \mathbf {b} ={\overrightarrow {CA}},\quad \mathbf {c} ={\overrightarrow {AB}}

соответственно. Отложим единичные векторы ${\overrightarrow {AK}}=\mathbf {c} _{1}$ и ${\overrightarrow {AL}}=\mathbf {b} _{1}$ на сторонах $AB$ и $AC$ соответственно и построим на этих ортах ромб $AKML$ (см. рисунок справа)^[37].

Диагональ $AM$ этого ромба — биссектриса угла $A$ . Вектор ${\overrightarrow {AP}}$ , направленный по биссектрисе угла $A$ , коллинеарен вектору $\mathbf {c} _{1}+(-\mathbf {b} _{1})$ :

{\overrightarrow {AP}}=x(\mathbf {c} _{1}-\mathbf {b} _{1})=x\left({\frac {\mathbf {c} }{|\mathbf {c} |}}-{\frac {\mathbf {b} }{|\mathbf {b} |}}\right),

где $x$ пока не определён^[37].

Либо таким же способом, то есть аналогично, либо заменой символов $a$ на $b$ , $b$ на $c$ , $c$ на $a$ , $x$ на $y$ , то есть циклической перестановкой, получается уравнение для вектора ${\overrightarrow {BP}}$ ^[37]:

{\overrightarrow {BP}}=y(\mathbf {a} _{1}-\mathbf {c} _{1})=y\left({\frac {\mathbf {a} }{|\mathbf {a} |}}-{\frac {\mathbf {c} }{|\mathbf {c} |}}\right).

Составим уравнение для нахождения $x$ и $y$ ^[37]:

{\overrightarrow {AP}}={\overrightarrow {AB}}+{\overrightarrow {BP}},

x\left({\frac {\mathbf {c} }{|\mathbf {c} |}}-{\frac {\mathbf {b} }{|\mathbf {b} |}}\right)=\mathbf {c} +y\left({\frac {\mathbf {a} }{|\mathbf {a} |}}-{\frac {\mathbf {c} }{|\mathbf {c} |}}\right).

В последнем уравнении нельзя приравнять коэффициенты при $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ , поскольку эти векторы компланарны, то есть

\mathbf {a} +\mathbf {b} +\mathbf {c} =\mathbf {0}

,

откуда выразим вектор $\mathbf {a}$ ^[37]:

\mathbf {a} =-\mathbf {b} -\mathbf {c} =\mathbf {0}

.

Теперь можно сократить количество векторов в уравнении до двух, исключив вектор $\mathbf {a}$ ^[37]:

x\left({\frac {\mathbf {c} }{|\mathbf {c} |}}-{\frac {\mathbf {b} }{|\mathbf {b} |}}\right)=\mathbf {c} +y\left(-{\frac {\mathbf {b} }{|\mathbf {a} |}}-{\frac {\mathbf {c} }{|\mathbf {a} |}}-{\frac {\mathbf {c} }{|\mathbf {c} |}}\right).

Поскольку разложение вектора по двум не коллинеарным векторам единственно, приравняем в последнем уравнении по отдельности коэффициенты при векторах $\mathbf {b}$ и $\mathbf {c}$ ^[39]:

-{\frac {x}{|\mathbf {b} |}}=-{\frac {y}{|\mathbf {a} |}},

{\frac {x}{|\mathbf {c} |}}=1-{\frac {y}{|\mathbf {a} |}}-{\frac {y}{|\mathbf {c} |}},

следовательно,

y={\frac {|\mathbf {a} ||\mathbf {c} |}{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}},\quad x={\frac {|\mathbf {b} ||\mathbf {c} |}{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}},

откуда

{\overrightarrow {AP}}={\frac {|\mathbf {b} |\mathbf {c} -|\mathbf {c} |\mathbf {b} }{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}},\quad {\overrightarrow {BP}}={\frac {|\mathbf {c} |\mathbf {a} -|\mathbf {a} |\mathbf {c} }{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}}.

Аналогично, если $P'$ — точка пересечения биссектрис $BB'$ и $CC'$ , то тогда

{\overrightarrow {BP'}}={\frac {|\mathbf {c} |\mathbf {a} -|\mathbf {a} |\mathbf {c} }{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}},\quad {\overrightarrow {CP'}}={\frac {|\mathbf {a} |\mathbf {b} -|\mathbf {b} |\mathbf {a} }{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}},

следовательно, ${\overrightarrow {BP}}={\overrightarrow {BP'}}$ , то есть точки $P$ и $P'$ совпадают и биссектрисы пересекаются в одной точке^[39].

Пусть теперь $\mathbf {r} _{1}={\overrightarrow {OA}}$ , $\mathbf {r} _{2}={\overrightarrow {OB}}$ и $\mathbf {r} _{3}={\overrightarrow {OC}}$ — радиус-векторы вершин соответственно $A$ , $B$ и $C$ треугольника $ABC$ , тогда радиус-вектор $\mathbf {r} ={\overrightarrow {OP}}$ точки пересечения биссектрис следующий^[39]:

\mathbf {r} =\mathbf {r} _{1}+{\overrightarrow {AP}}={\frac {(|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |)\mathbf {r} _{1}}{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}}+{\frac {|\mathbf {b} |(\mathbf {r} _{2}-\mathbf {r} _{1})-|\mathbf {c} |(\mathbf {r} _{1}-\mathbf {r} _{3})}{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}}=

={\frac {|\mathbf {a} |\mathbf {r} _{1}+|\mathbf {b} |\mathbf {r} _{2}+|\mathbf {c} |\mathbf {r} _{3}}{|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |}}.

Задача 9. В треугольнике $ABC$ точки $A'$ , $B'$ и $C'$ лежат произвольно на сторонах $BC$ , $CA$ и $AB$ соответственно. Найти соотношение между шестью отрезками $AC'$ , $C'B$ , $BA'$ , $A'C$ , $CB'$ и $B'C$ , при которых прямые $AA'$ , $BB'$ и $CC'$ пересекаются в одной точке $P$ ^[40].

Решение^[41]

Треугольник и три прямые, пересекающиеся в одной точке

Поместим точку $O$ вне плоскости треугольника $ABC$ , и пусть $\mathbf {r} _{1}={\overrightarrow {OA}}$ , $\mathbf {r} _{2}={\overrightarrow {OB}}$ и $\mathbf {r} _{3}={\overrightarrow {OC}}$ — радиус-векторы соответствующих вершин треугольника, а $\mathbf {r} ={\overrightarrow {P}}$ — радиус-вектор точки $P$ пересечения трёх прямых $AA'$ , $BB'$ и $CC'$ (см. рисунок справа). Разложим вектор $\mathbf {r}$ по трём некомпланарным векторам $\mathbf {r} _{1}$ , $\mathbf {r} _{2}$ и $\mathbf {r} _{3}$ ^[41]:

\mathbf {r} =\alpha _{1}\mathbf {r} _{1}+\alpha _{2}\mathbf {r} _{2}+\alpha _{3}\mathbf {r} _{3}

,

причём, по задаче 2,

\alpha _{1}+\alpha _{2}+\alpha _{3}=1

.

Александров П. С. Лекции по аналитической геометрии, пополненные необходимыми сведениями из алгебры с приложением собрания задач, снабжённых решениями, составленного А. С, Пархоменко. 2-е изд. М.: Наука, 1968. 912 с., ил.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия. 7—9 классы : учебник для общеобразовательных организаций. 2-е изд. М.: Просвещение, 2014. 383 с., ил.
Болтянский В. Г., Яглом И. М. Векторы и их применения в геометрии // Энциклопедия элементарной математики, книга четвёртая — геометрия / Гл. ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. Ред. книги 4: В. Г. Болтянский, И. М. Яглом. М.: Физматгиз, 1963. 568 с., ил. С. 291—381.
Векторное исчисление // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 109.
Выгодский М. Я. Справочник по высшей математике. Изд-е 12-е, стереотип. М.: Наука, 1977. 871 с., ил.
Вычитание // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 1 А—Г. М.: «Советская Энциклопедия», 1977. 1152 стб., ил. Стб. 828.
Вычитание // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 135.
Кочин Г. Ф. Векторное исчисление и начала тензорного исчисления. Изд-е 9-е. М.: Наука, 1965. 427 с., ил.
Лаптев Г. Ф. Элементы векторного исчисления. М.: Наука, 1975. 336 с., ил.
Линейные операции // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 320.
Линейные операции над векторами // Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Математический словарь высшей школы: Общая часть / Под. ред. Ю. С. Богданова. Минск: Высшая школа, 1984. 527 с., ил. С. 186.
Пытьев Ю. П. Векторная алгебра // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 1 А—Г. М.: «Советская Энциклопедия», 1977. 1152 стб., ил. Стб. 632—636.
Разность векторов // Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Математический словарь высшей школы: Общая часть / Под. ред. Ю. С. Богданова. Минск: Высшая школа, 1984. 527 с., ил. С. 369.
Сложение векторов // Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Математический словарь высшей школы: Общая часть / Под. ред. Ю. С. Богданова. Минск: Высшая школа, 1984. 527 с., ил. С. 412.
Умножение вектора на число // Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Математический словарь высшей школы: Общая часть / Под. ред. Ю. С. Богданова. Минск: Высшая школа, 1984. 527 с., ил. С. 462.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

Линейная операция

Определение

Сложение векторов

Законы сложения

Вычитание векторов

Умножение вектора на число

Законы умножения на скаляр

Разложение вектора

Применение линейных операций

Коллинеарность и компланарность точек

Построение треугольника

Середина отрезка

Пересечение трёх прямых в одной точке

Примечания

Источники

Категории