Параллелограмм

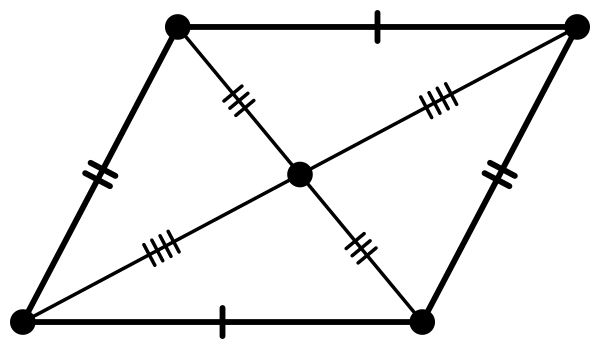
• Противолежащие стороны параллелограмма равны.
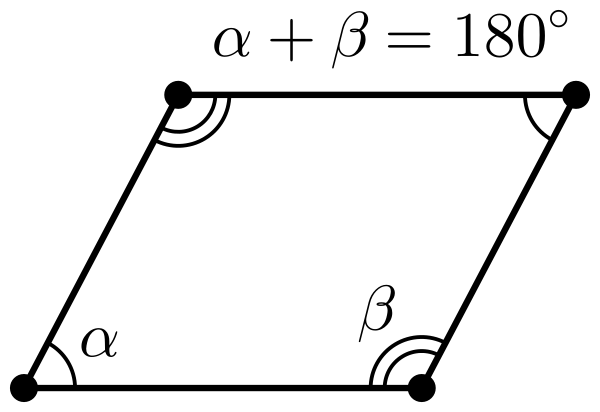
• Противолежащие углы параллелограмма равны.
• Сумма углов, прилежащих к одной (любой) стороне, равна 180° (по свойству параллельных прямых).
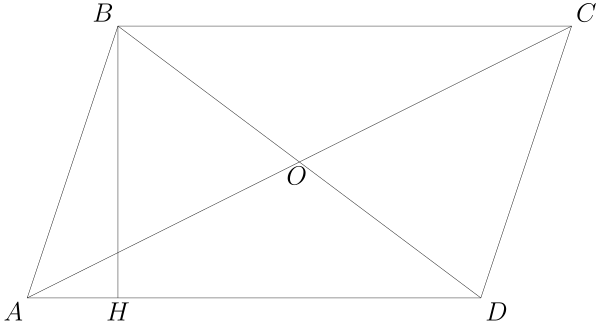
• Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

  ${\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}$.

• Точка пересечения диагоналей является центром симметрии параллелограмма.
• Параллелограмм диагональю делится на два равных треугольника.
• Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
• Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть

${\displaystyle a}$ — длина стороны ${\displaystyle AB}$,

${\displaystyle b}$ — длина стороны ${\displaystyle BC}$,

${\displaystyle d_{1}}$ и ${\displaystyle d_{2}}$ — длины диагоналей; тогда:

${\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}$

Тождество параллелограмма есть простое следствие формулы Эйлера для произвольного четырёхугольника: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей. У параллелограмма противоположные стороны равны, а расстояние между серединами диагоналей равно нулю.

• Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.
• В параллелограмме отношение меньшей из смежных сторон к большей из этих сторон не меньше тангенса половины угла между диагоналями данного параллелограмма. И указанное отношение равно указанному тангенсу тогда и только тогда, когда этот параллелограмм — прямоугольник или ромб.
• Угол между диагоналями произвольного параллелограмма (не тупой угол) содержит в своей внутренней области меньшую из смежных сторон данного параллелограмма.
• Диагонали ${\displaystyle d_{1}\leqslant d_{2}}$ параллелограмма, отличного от ромба, выражаются через длины ${\displaystyle a}$ и ${\displaystyle b}$ его смежных сторон и угол ${\displaystyle \theta }$ между диагоналями данного параллелограмма, содержащий во внутренней области сторону ${\displaystyle b}$:

${\displaystyle d_{1}={\sqrt {\frac {{\bigl (}a\cos {\frac {\theta }{2}}{\bigr )}^{2}-{\bigl (}b\sin {\frac {\theta }{2}}{\bigr )}^{2}}{\cos \theta }}}-{\sqrt {\frac {{\bigl (}b\cos {\frac {\theta }{2}}{\bigr )}^{2}-{\bigl (}a\sin {\frac {\theta }{2}}{\bigr )}^{2}}{\cos \theta }}}={\sqrt {a^{2}+b^{2}-{\sqrt {(2ab)^{2}-{\bigl (}(a^{2}-b^{2})\operatorname {tg} \theta {\bigr )}^{2}}}}}}$;

${\displaystyle d_{2}={\sqrt {\frac {{\bigl (}a\cos {\frac {\theta }{2}}{\bigr )}^{2}-{\bigl (}b\sin {\frac {\theta }{2}}{\bigr )}^{2}}{\cos \theta }}}+{\sqrt {\frac {{\bigl (}b\cos {\frac {\theta }{2}}{\bigr )}^{2}-{\bigl (}a\sin {\frac {\theta }{2}}{\bigr )}^{2}}{\cos \theta }}}={\sqrt {a^{2}+b^{2}+{\sqrt {(2ab)^{2}-{\bigl (}(a^{2}-b^{2})\operatorname {tg} \theta {\bigr )}^{2}}}}}}$.

• Угол ${\displaystyle \theta }$ между диагоналями произвольного параллелограмма (не тупой угол) является любым одним из положительных решений неравенства:

${\displaystyle \theta \leqslant \arccos {\frac {|k^{2}-1|}{k^{2}+1}}}$,

где ${\displaystyle k}$ — везде одно и то же отношение смежных сторон параллелограмма. Равенство здесь достигается тогда и только тогда, когда данный параллелограмм — прямоугольник (если при этом ${\displaystyle k\neq 1}$) или ромб (если ${\displaystyle k=1}$).

• Высоты ${\displaystyle h_{a}}$ и ${\displaystyle h_{b}}$, проведённые соответственно к сторонам ${\displaystyle a}$ и ${\displaystyle b}$ параллелограмма, который отличен от ромба и угол между диагоналями которого равен ${\displaystyle \theta }$, могут быть найдены по формулам:

${\displaystyle h_{a}={\frac {|a^{2}-b^{2}|\operatorname {tg} \theta }{2a}}}$;

${\displaystyle h_{b}={\frac {|a^{2}-b^{2}|\operatorname {tg} \theta }{2b}}}$. Здесь ${\displaystyle \theta }$ — угол, во внутренней области которого расположена меньшая из смежных сторон ${\displaystyle a}$, ${\displaystyle b}$ такого параллелограмма.

• Угол ${\displaystyle \alpha }$ (не тупой) между смежными сторонами параллелограмма, отличного от ромба, выражается через длины смежных сторон ${\displaystyle a}$, ${\displaystyle b}$ и угол ${\displaystyle \theta }$ (острый) между диагоналями данного параллелограмма как:

${\displaystyle \alpha =\arcsin {\frac {|a^{2}-b^{2}|\operatorname {tg} \theta }{2ab}}}$.

• Угол ${\displaystyle \theta }$ (острый) между диагоналями параллелограмма, отличного от ромба, выражается через длины смежных сторон ${\displaystyle a}$, ${\displaystyle b}$ и угол ${\displaystyle \alpha }$ между ними по формуле:

${\displaystyle \theta =\operatorname {arctg} {\frac {2ab\sin \alpha }{|a^{2}-b^{2}|}}=\operatorname {arctg} {\frac {2S}{|a^{2}-b^{2}|}}}$,

где ${\displaystyle S}$ — площадь данного параллелограмма.

• И ещё, если ${\displaystyle d_{1}}$ и ${\displaystyle d_{2}}$ — диагонали данного параллелограмма, а ${\displaystyle a}$ и ${\displaystyle b}$ — смежные его стороны, то угол ${\displaystyle \theta }$ между диагоналями этого параллелограмма, содержащий во внутренней области сторону ${\displaystyle b}$, можно найти как:

${\displaystyle \theta =\arccos {\frac {a^{2}-b^{2}}{d_{1}d_{2}}}}$.

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий (в этом случае выполняются и все остальные):

1. У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: ${\displaystyle AB=CD,AB\parallel CD}$.
2. Все противоположные углы попарно равны: ${\displaystyle \angle A=\angle C,\angle B=\angle D}$.
3. У четырёхугольника без самопересечений все противоположные стороны попарно равны: ${\displaystyle AB=CD,BC=DA}$.
4. Все противоположные стороны попарно параллельны: ${\displaystyle AB\parallel CD,BC\parallel DA}$.
5. Диагонали делятся в точке их пересечения пополам: ${\displaystyle AO=OC,BO=OD}$.
6. Сумма расстояний между серединами противоположных сторон выпуклого четырёхугольника равна его полупериметру.
7. Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: ${\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}$.

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для площади произвольных четырёхугольников.

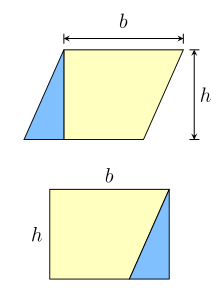
• Площадь параллелограмма равна произведению его основания на высоту:

${\displaystyle S=bh}$ , где ${\displaystyle b}$ — сторона, ${\displaystyle h}$ — высота, проведённая к этой стороне.

• Площадь параллелограмма равна произведению длин его смежных сторон и синуса угла между ними:

${\displaystyle S=ab\sin \alpha ,}$

где ${\displaystyle a}$ и ${\displaystyle b}$ — смежные стороны, ${\displaystyle \alpha }$ — угол между сторонами ${\displaystyle a}$ и ${\displaystyle b}$.

• Также площадь параллелограмма может быть выражена через стороны ${\displaystyle a,\ b}$ и длину любой из диагоналей ${\displaystyle d}$ по формуле Герона как сумма площадей двух равных примыкающих треугольников^[3]:

${\displaystyle S=2\cdot {\sqrt {p(p-a)(p-b)(p-d)}}}$,

где ${\displaystyle p=(a+b+d)/2.}$

• Если параллелограмм отличен от ромба, через длины смежных сторон ${\displaystyle a}$ и ${\displaystyle b}$ и угол ${\displaystyle \theta }$ между диагоналями данного параллелограмма можно определить:

${\displaystyle S={\frac {|a^{2}-b^{2}|\operatorname {tg} \theta }{2}}}$. Здесь ${\displaystyle \theta }$ — угол, во внутренней области которого расположена меньшая из смежных сторон этого параллелограмма.

• Площадь параллелограмма через длины ${\displaystyle d_{1}}$ и ${\displaystyle d_{2}}$ его диагоналей и длины его смежных сторон: ${\displaystyle a}$ и ${\displaystyle b}$:

${\displaystyle S={\frac {\sqrt {(d_{1}d_{2})^{2}-(a^{2}-b^{2})^{2}}}{2}}}$.