Метод трапеций

Пусть функция ${\displaystyle f(x)}$ определена на отрезке ${\displaystyle [a,b]}$, где ${\displaystyle a<b}$. Этот отрезок разбит на ${\displaystyle n}$ частей произвольными точками ${\displaystyle a=x_{0}<x_{1}<x_{2}<\ldots <x_{n}=b}$, и пусть ${\displaystyle \Delta x_{k}=x_{k}-x_{k-1}}$${\displaystyle (\Delta x_{k}>0)}$ — длины полученных частичных отрезков ${\displaystyle [x_{k-1},x_{k}]}$. В каждом частичном отрезке ${\displaystyle [x_{k-1},x_{k}]}$ есть произвольная точка ${\displaystyle \xi _{k}}$. Сумма значений заданной функции в этих точках ${\displaystyle f(\xi _{k})}$ называется интегральной суммой функции ${\displaystyle f(x)}$ нa заданном отрезке ${\displaystyle \sum \limits _{k=1}^{n}f(\xi _{k})\Delta x_{k}}$.

Если при любых разбиениях отрезка ${\displaystyle [a,b]}$, (${\displaystyle a<b}$) на частичные отрезки ${\displaystyle [x_{k-1},x_{k}]}$ (наибольший из которых имеет длину ${\displaystyle \lambda }$) и при любом выборе точек ${\displaystyle \xi _{k}}$ в них интегральные суммы ${\displaystyle \sum \limits _{k=1}^{n}f(\xi _{k})\Delta x_{k}}$ при ${\displaystyle \lambda \rightarrow 0}$ имеют один и тот же конечный предел, то этот предел называют определённым интегралом в смысле Римана от функции ${\displaystyle f(x)}$ по отрезку ${\displaystyle [a,b]}$ и записывают как ${\displaystyle \int \limits _{a}^{b}f(x)dx=\lim \limits _{\lambda \rightarrow 0}\sum \limits _{k=1}^{n}f(\xi _{k})\Delta x_{k}}$.

Функция ${\displaystyle f(x)}$ называется подынтегральной функцией^[1].

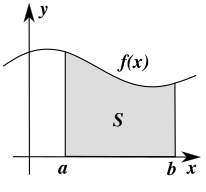
Определённый интеграл от неотрицательной функции ${\displaystyle \int \limits _{a}^{b}f(x)\,dx}$ численно равен площади фигуры, ограниченной осью абсцисс, прямыми ${\displaystyle x=a}$ и ${\displaystyle x=b}$ и графиком функции ${\displaystyle f(x)}$, называемой криволинейной трапецией (рис. 1).

Рис. 1

Существует несколько методов вычисления интегралов. Так, непосредственное интегрирование — это метод, при котором интеграл путём тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким интегралам элементарных функций. В случаях, когда непосредственное вычисление интегралов затруднительно, прибегают к их приближённому вычислению. Так, например, при решении физических задач приходится иметь дело с определёнными интегралами от непрерывных функций, первообразные которых не выражаются через элементарные функции. Это приводит к необходимости получения приближённых формул для вычисления определённых интегралов.

К наиболее употребительным методам приближённых вычислений относятся: метод прямоугольников, метод трапеций, метод Симпсона. Основная идея этих методов заключается в замене подынтегральной функции ${\displaystyle f(x)}$ многочленом, значения которого совпадают со значениями функции ${\displaystyle f(x)}$в некоторых точках^[2].

Пусть требуется вычислить интеграл ${\displaystyle \int _{a}^{b}f(x)dx}$, где функция ${\displaystyle f(x)}$ непрерывна на отрезке ${\displaystyle [a,b]}$.

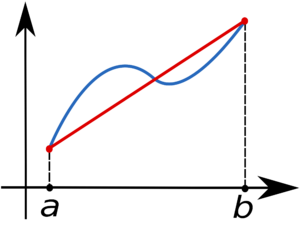
Заменив функцию ${\displaystyle f(x)}$ многочленом первого порядка, а именно линейной функцией ${\displaystyle y=kx+b}$, совпадающей с ${\displaystyle f(x)}$ в точках ${\displaystyle a}$ и ${\displaystyle b}$, получают приближённое значение интеграла ${\displaystyle \int _{a}^{b}f(x)dx}$, равное площади прямоугольной трапеции; ${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {f(a)+f(b)}{2}}(b-a)}$.

Рис. 2

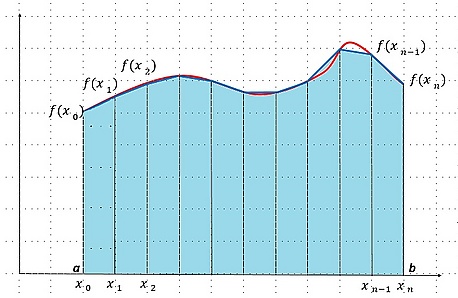
Пусть отрезок ${\displaystyle \left[a,b\right]}$ разбит на ${\displaystyle n}$ равных частей точками ${\displaystyle a=x_{0}<x_{1}<x_{2}<...<x_{n-1}<x_{n}=b}$ и с помощью прямых ${\displaystyle x=x_{k}(k=0,1,2,...,n)}$ построены ${\displaystyle n}$ прямолинейных трапеций (рис. 3). Тогда сумма площадей этих трапеций приближённо равна ${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {f(x_{0})+f(x_{1})}{2}}(x_{1}-x_{0})+{\frac {f(x_{1})+f(x_{2})}{2}}(x_{2}-x_{1})+...+{\frac {f(x_{n-1})+f(x_{n})}{2}}(x_{n}-x_{n-1})={\frac {b-a}{2n}}\left[f(a)+f(b)+2\sum _{k=1}^{n-1}f(x_{k})\right]}$, где ${\displaystyle f(x_{k-1})}$ и ${\displaystyle f(x_{k})}$ — соответственно основания трапеций, а ${\displaystyle x_{k}-x_{k-1}={\frac {b-a}{n}}}$ — их высоты (рис. 3).

Рис. 3

Таким образом, формула трапеций имеет вид: ${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{2n}}\left[f(a)+f(b)+2\sum _{k=1}^{n-1}f(x_{k})\right]}$.

Замечание: Если функция ${\displaystyle f(x)}$ имеет на ${\displaystyle \left[a,b\right]}$ непрерывную производную второго порядка ${\displaystyle f''(x)}$, то абсолютная величина погрешности не превосходит числа ${\displaystyle M{\frac {(b-a)^{3}}{12n^{2}}}}$, где ${\displaystyle M=\max _{a\leqslant x\leqslant b}|f''(x)|}$^[3].

Формулы приближённого вычисления определённого интеграла имеют вид приближённых равенств, в левой части которых стоит вычисляемый интеграл, а в правой — обобщение суммы Римана: линейная комбинация с постоянными коэффициентами значений подынтегральной функции в точках области интегрирования, называемых узлами. При ${\displaystyle n=1}$ такие формулы приближённого интегрирования называют квадратурными. В основу получения квадратурных формул положено требование, чтобы приближённое равенство обращалось в точное, когда подынтегральная функция является многочленом степени не выше ${\displaystyle m}$. Для краткости говорят, что квадратурная формула обладает ${\displaystyle m}$-свойством. Оно удачно учитывает индивидуальность подынтегральной функции: чем лучше функция может быть приближена многочленом, тем точнее результат вычисления интеграла с помощью квадратурной формулы^[4]. Простейшими квадратурными формулами являются формула прямоугольников и формула трапеций, которые дают точное значение интеграла для линейных функций^[5].

В левой части квадратурной формулы стоит интеграл, подлежащий вычислению. Подынтегральная функция записана в виде произведения, где ${\displaystyle p(x)}$ фиксирована для данной квадратурной формулы и называется весовой функцией. Сумма в правой части называется квадратурной суммой, числа ${\displaystyle x_{j}}$ называются узлами квадратурной формулы, а числа ${\displaystyle C_{j}}$ — коэффициентами:${\displaystyle \int _{a}^{b}p(x)f(x)dx=\sum _{j=1}^{N}C_{j}f(x_{j})}$^[6].

При равноотстоящих узловых точках получаются формулы, называемые формулами Ньютона — Котеса: ${\displaystyle \int _{a}^{b}f(x)\,dx={\frac {nh}{P_{n}}}\sum _{j=0}^{n}f(a+jh)p_{jn}+R_{n}[f]}$, где ${\displaystyle {P_{n}}=\sum _{j=0}^{n}p_{jn}}$, ${\displaystyle h={\frac {b-a}{n}}}$, ${\displaystyle a=x_{0}}$, ${\displaystyle x_{n}=b}$.

При ${\displaystyle n=1}$ приведённая выше формула называется формулой трапеций^[7].