Обратные тригонометрические функции

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки арк- . Эта приставка является частью латинского слова arcus, которое означает «лук, дуга, дугоподобная линия». В русской математической литературе слово аркус встречается с 1718 г.^[1]. В этом значении понятие обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу).

Первым автором, который использовал специальные символы для обратных тригонометрических функций был Д. Бернулли. В 1729 и в 1736 гг. он писал ${\displaystyle AS}$ и ${\displaystyle At}$ соответственно вместо ${\displaystyle \arcsin }$ и ${\displaystyle \operatorname {arctg} }$. Современные обозначения ${\displaystyle \arcsin x}$ и ${\displaystyle \operatorname {arctg} x}$ появились в 1772 г. в трудах венского математика К. Шерфера и закрепились благодаря Лагранжу. Обозначения были приняты сразу только французскими математиками (Кондорсе — 1772, Ламберт — 1776). В качестве других примеров можно привести ${\displaystyle \sin ^{-1}x}$, ${\displaystyle \cos ^{-1}x}$ Гершеля (1813) или ${\displaystyle {\frac {1}{\sin }}x}$, ${\displaystyle {\frac {1}{\cos }}x}$ Мартина Ома (1829). Современные обозначения утвердились только к концу XIX века^[2].

Функции, обратные к тригонометрическим функциям, называются обратными круговыми или обратными тригонометрическими функциями. Пусть k — целое число.

Функции, обратные к функциям ${\displaystyle {\begin{Bmatrix}y=\sin x\\y=\cos x\\y=\operatorname {tg} x\\y=\operatorname {ctg} x\end{Bmatrix}}}$, принадлежащие каждому промежутку ${\displaystyle {\begin{Bmatrix}\left[{\frac {2k-1}{2}}\pi ,{\frac {2k+1}{2}}\pi \right]\\\left[k\pi ,(k+1)\pi \right]\\\left({\frac {2k-1}{2}}\pi ,{\frac {2k+1}{2}}\pi \right)\\\left(k\pi ,(k+1)\pi \right)\end{Bmatrix}}}$, называются арксинусом, арккосинусом, арктангенсом, арккотангенсом и обозначаются ${\displaystyle {\begin{Bmatrix}y=\operatorname {Arcsin} x\\y=\operatorname {Arccos} x\\y=\operatorname {Arctg} x\\y=\operatorname {Arcctg} x\end{Bmatrix}}}$.

Поскольку тригонометрические функции периодичны, обратные к ним функции являются многозначными. Если положить в вышеприведённых интервалах ${\displaystyle k=0}$ , то получаются обратные тригонометрические функции, которые применяются наиболее часто (так называемые главные значения). Они обозначаются соответственно ${\displaystyle \arcsin x}$, ${\displaystyle \arccos x}$, ${\displaystyle \operatorname {arctg} x}$, ${\displaystyle \operatorname {arcctg} x}$^[3].

Арксинусом числа ${\displaystyle a}$ называется такое число из отрезка ${\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}$, синус которого равен ${\displaystyle a}$. Другими словами, ${\displaystyle \arcsin a}$ — дуга, синус которой равен ${\displaystyle a}$^[4].

• Область определения: ${\displaystyle [-1;1]}$ .
• Область значений:${\displaystyle \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}$.
• Чётность/нечётность: ${\displaystyle \arcsin(-x)=-\arcsin x}$ — функция нечётная .
• Нули: ${\displaystyle x_{0}=0}$.
• Промежутки знакопостоянства: ${\displaystyle \arcsin x>0}$ при ${\displaystyle 0<x\leqslant 1}$; ${\displaystyle \arcsin x<0}$ при ${\displaystyle -1\leqslant x<0.}$
• Промежутки монотонности: функция возрастает на всей области определения.
• Экстремумы: нет.
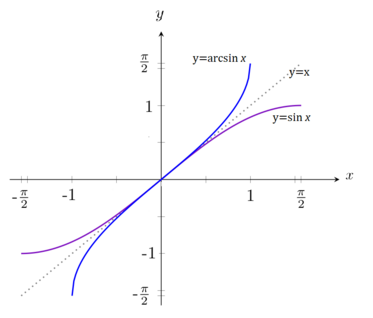
• График функции— часть синусоиды, зеркально отражённой относительно прямой ${\displaystyle y=x}$ (биссектрисы первого и третьего квадрантов). График имеет в начале координат точку перегиба^[5]. (Рис. 1).

Рис. 1

Арккосинусом числа ${\displaystyle a}$ называется такое число из отрезка ${\displaystyle \left[0;\pi \right]}$, косинус которого равен ${\displaystyle a}$. Другими словами, ${\displaystyle \arccos a}$ — дуга, косинус которой равен ${\displaystyle a}$^[6].

• Область определения: ${\displaystyle [-1;1]}$ .
• Область значений:${\displaystyle \left[0;\pi \right]}$.
• Чётность/нечётность: функция не является ни чётной, ни нечётной.
• Нули: ${\displaystyle x_{0}=1}$.
• Промежутки знакопостоянства: ${\displaystyle \arccos x>0}$ при ${\displaystyle -1\leqslant x<1.}$
• Промежутки монотонности: функция убывает на всей области определения.
• Экстремумы: нет.
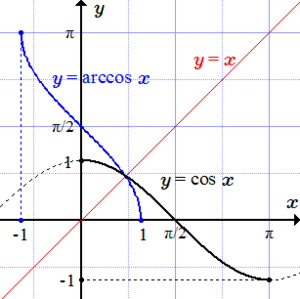
• График функции— часть косинусоиды, зеркально отражённой относительно прямой ${\displaystyle y=x}$ — имеет в точке${\displaystyle (0;{\frac {\pi }{2}})}$ точку перегиба^[5]. (Рис. 2).

Рис. 2

• ${\displaystyle \arccos x=\left\{{\begin{matrix}\arcsin {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\\pi -\arcsin {\sqrt {1-x^{2}}},\qquad -1\leqslant x\leqslant 0\end{matrix}}\right.}$
• ${\displaystyle \arccos x=\operatorname {arcctg} {\frac {x}{\sqrt {1-x^{2}}}}}$
• ${\displaystyle \arccos x=\left\{{\begin{matrix}\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\pi +\operatorname {arctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad -1\leqslant x<0\end{matrix}}\right.}$
• ${\displaystyle \arccos x=2\arcsin {\sqrt {\frac {1-x}{2}}}}$
• ${\displaystyle \arccos x=2\arccos {\sqrt {\frac {1+x}{2}}}}$
• ${\displaystyle \arccos x=2\operatorname {arctg} {\sqrt {\frac {1-x}{1+x}}}}$.

Арктангенсом числа ${\displaystyle a}$ называется такое число из интервала ${\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)}$, тангенс которого равен ${\displaystyle a}$.

• Область определения: ${\displaystyle \mathbb {R} }$.
• Область значений:${\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)}$.
• Чётность/нечётность: ${\displaystyle \operatorname {arctg} (-x)=-\operatorname {arctg} x}$ — функция нечётная.
• Нули: ${\displaystyle x_{0}=0}$.
• Промежутки знакопостоянства: ${\displaystyle \operatorname {arctg} x>0}$ при ${\displaystyle x>0}$; ${\displaystyle \operatorname {arctg} x<0}$ при ${\displaystyle x<0}$.
• Промежутки монотонности: функция возрастает на всей области определения.
• Экстремумы: нет^[7].
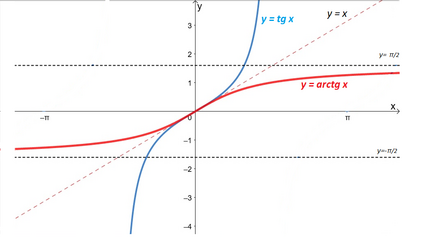
• График функции получают зеркальным отражением графика соответствующей ветви функции ${\displaystyle y=\operatorname {tg} x}$ относительно прямой ${\displaystyle y=x}$. В начале координат функция имеет точку перегиба.
• Асимптоты: прямые ${\displaystyle y=-{\frac {\pi }{2}}}$ и ${\displaystyle y={\frac {\pi }{2}}}$^[8]. (Рис. 3).

Рис. 3

• ${\displaystyle \operatorname {arctg} x=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}.}$
• ${\displaystyle \operatorname {arctg} x=\left\{{\begin{matrix}\arccos {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\geqslant 0\\-\arccos {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\leqslant 0\end{matrix}}\right.}$
• ${\displaystyle \operatorname {arctg} x=\pi /2-\operatorname {arcctg} x.}$
• ${\displaystyle \operatorname {arctg} x=\left\{{\begin{matrix}\operatorname {arcctg} {\frac {1}{x}},\qquad x>0\\\operatorname {arcctg} {\frac {1}{x}}-\pi ,\qquad x<0\end{matrix}}\right.}$.

Арккотангенсом числа ${\displaystyle a}$ называется такое число из интервала ${\displaystyle \left(0;\pi \right)}$, котангенс которого равен ${\displaystyle a}$.

• Область определения: ${\displaystyle \mathbb {R} }$.
• Область значений: ${\displaystyle (0;\pi )}$.
• Чётность/нечётность: функция не является ни чётной, ни нечётной.
• Нули: нет.
• Промежутки знакопостоянства: ${\displaystyle \operatorname {arcctg} x>0}$ при любых ${\displaystyle x.}$
• Промежутки монотонности: функция убывает на всей области определения.
• Экстремумы: нет^[9].
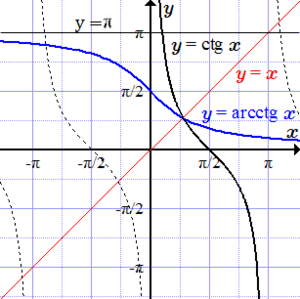
• График функции получают зеркальным отражением графика соответствующей ветви функции ${\displaystyle y=\operatorname {tg} x}$ относительно прямой ${\displaystyle y=x}$. В точке ${\displaystyle (0;{\frac {\pi }{2}})}$ функция имеет точку перегиба.
• Асимптоты: прямые ${\displaystyle y=0}$ и ${\displaystyle y=\pi }$^[8]. (Рис. 4).

Рис. 4

• ${\displaystyle \operatorname {arcctg} x=\arccos {\frac {x}{\sqrt {1+x^{2}}}}.}$
• ${\displaystyle \operatorname {arcctg} x=\left\{{\begin{matrix}\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\geqslant 0\\\pi -\arcsin {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\leqslant 0\end{matrix}}\right.}$
• ${\displaystyle \operatorname {arcctg} x=\pi /2-\operatorname {arctg} x.}$
• ${\displaystyle \operatorname {arcctg} x=\left\{{\begin{matrix}\operatorname {arctg} {\frac {1}{x}},\qquad x>0\\\operatorname {arctg} {\frac {1}{x}}+\pi ,\qquad x<0\end{matrix}}\right.}$.

Функции ${\displaystyle \operatorname {arcsec} x}$ и ${\displaystyle \operatorname {arccosec} x}$ являются малоупотребительными.

• ${\displaystyle \arcsin(-x)=-\arcsin x}$;
• ${\displaystyle \arccos(-x)=\pi -\arccos x}$;
• ${\displaystyle \operatorname {arctg} (-x)=-\operatorname {arctg} x}$;
• ${\displaystyle \operatorname {arcctg} (-x)=\pi -\operatorname {arcctg} x}$;
• ${\displaystyle \operatorname {arccosec} (-x)=-\operatorname {arccosec} x}$;
• ${\displaystyle \operatorname {arcsec} (-x)=\pi -\operatorname {arcsec} x}$^[10].

• ${\displaystyle \displaystyle \arcsin x=x+\sum _{n=1}^{\infty }{\frac {(2n-1)!!}{2n!!(2n+1)}}x^{2n+1}}$ , для ${\displaystyle \left|x\right|<1}$;
• ${\displaystyle \displaystyle \operatorname {arctg} \ x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}}$, для ${\displaystyle \left|x\right|<1}$^[11].

Для действительных и комплексных x:

${\displaystyle {\begin{aligned}\int \arcsin x\,dx&{}=x\,\arcsin x+{\sqrt {1-x^{2}}}+C,\\\int \arccos x\,dx&{}=x\,\arccos x-{\sqrt {1-x^{2}}}+C,\\\int \operatorname {arctg} \,x\,dx&{}=x\,\operatorname {arctg} \,x-{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arcctg} \,x\,dx&{}=x\,\operatorname {arcctg} \,x+{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\,\right)\!\right)+C,\\\int \operatorname {arccosec} \,x\,dx&{}=x\,\operatorname {arccosec} \,x+\ln \left(x\left(1+{\sqrt {{x^{2}-1} \over x^{2}}}\,\right)\!\right)+C.\end{aligned}}}$

Для действительных x ≥ 1:

${\displaystyle {\begin{aligned}\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C,\\\int \operatorname {arccosec} \,x\,dx&{}=x\,\operatorname {arccosec} \,x+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C.\end{aligned}}}$

См. также Список интегралов от обратных тригонометрических функций.

Обратные тригонометрические функции комплексного переменного ${\displaystyle z=x+iy}$ определяются как аналитические продолжения соответствующих обратных тригонометрических функций действительного переменного в комплексную плоскость^[12].

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

${\displaystyle {\begin{aligned}\arcsin z&{}=-i\ln(iz+{\sqrt {1-z^{2}}})={\frac {\pi }{2}}-i\ln(z+{\sqrt {z^{2}-1}})=-i\operatorname {arsh} \,iz,\end{aligned}}}$

${\displaystyle \arccos(z)={\dfrac {\pi }{2}}+i\ln(iz+{\sqrt {1-z^{2}}})=-i\operatorname {arch} (iz)}$

${\displaystyle \operatorname {arctg} (z)={\dfrac {i}{2}}(\ln(1-iz)-\ln(1+iz))=-i\operatorname {arth} (iz)}$

${\displaystyle \operatorname {arcctg} (z)={\dfrac {i}{2}}\left(\ln \left({\dfrac {z-i}{z}}\right)-\ln \left({\dfrac {z+i}{z}}\right)\right)=i\operatorname {arcth} (iz)}$

${\displaystyle \operatorname {arcsec} (z)=\arccos \left(z^{-1}\right)={\dfrac {\pi }{2}}+i\ln \left({\sqrt {1-{\dfrac {1}{z^{2}}}}}+{\dfrac {i}{z}}\right),}$

${\displaystyle \operatorname {arccosec} \,(z)=\arcsin \left(z^{-1}\right)=-i\ln \left({\sqrt {1-{\dfrac {1}{z^{2}}}}}+{\dfrac {i}{z}}\right).}$