Чётность и нечётность функции

Узнать больше

Узнать больше в энциклопедической статье

Перейти

Узнать больше

Узнать больше в энциклопедической статье

Перейти

Материал ОГЭ/ЕГЭ

База знаний для подготовки к ЕГЭ и ОГЭ, проверенная Российской Академией наук

Подробнее

Материал ОГЭ/ЕГЭ

База знаний для подготовки к ЕГЭ и ОГЭ, проверенная Российской Академией наук

Подробнее

Функция называется чётной при одновременном выполнении двух условий:

1. область определения функции обладает симметрией относительно начала координат,
2. для аргументов с одинаковым модулем и противоположным знаком сохраняется одинаковое значение функции, то есть ${\displaystyle f(x)=f(-x)}$.

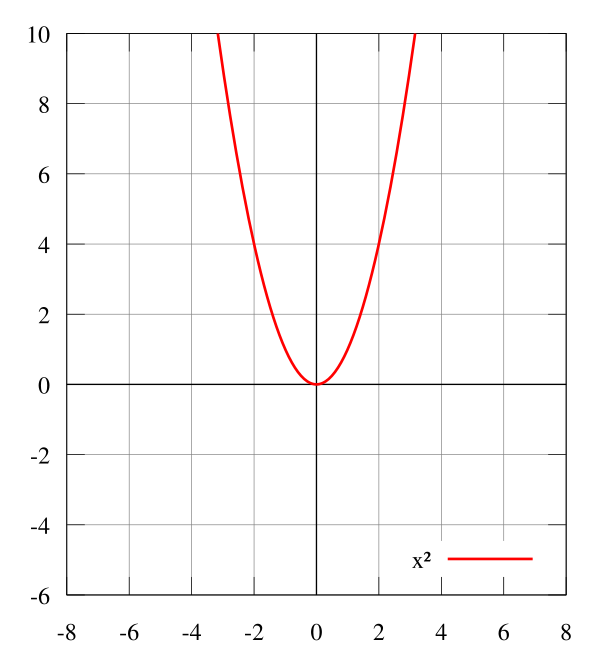
В качестве примера чётной функции приводят квадратичную функцию вида ${\displaystyle y(x)=x^{2}}$. В этом случае значение функции зависит только от модуля аргумента и не меняется при изменении его знака, поскольку возведение в квадрат даёт неотрицательный результат.

График любой чётной функции симметричен относительно оси ОУ. К числу таких функций относятся: степенная функция с чётным показателем степени (например, ${\displaystyle y=-x^{4}}$, график которой представляет собой перевёрнутую параболу), тригонометрическая функция ${\displaystyle y=\cos(x)}$, а также функции, в которых «x» заключён под знаком модуля (например, ${\displaystyle y={\frac {3}{2+|x|}}}$).

Функция называется нечётной при выполнении двух условий:

1. область значения функции симметрична относительно начала координат,
2. выполняется соотношение ${\displaystyle f(-x)=-f(x)}$.

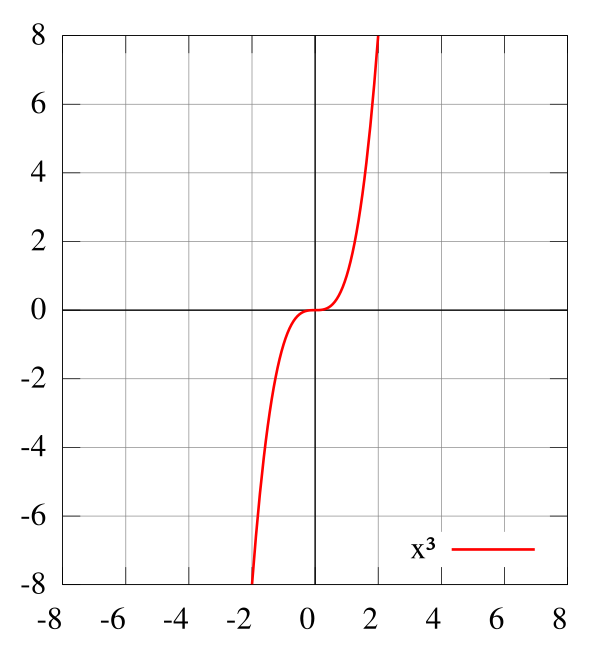
Примерами нечётных функций являются линейная функция ${\displaystyle y=x}$, степенная функция с нечётным показателем степени (например, ${\displaystyle y=x^{3}}$), обратная пропорциональность ${\displaystyle y={\frac {1}{x}}}$ и тригонометрическая функция ${\displaystyle y=\sin(x)}$.

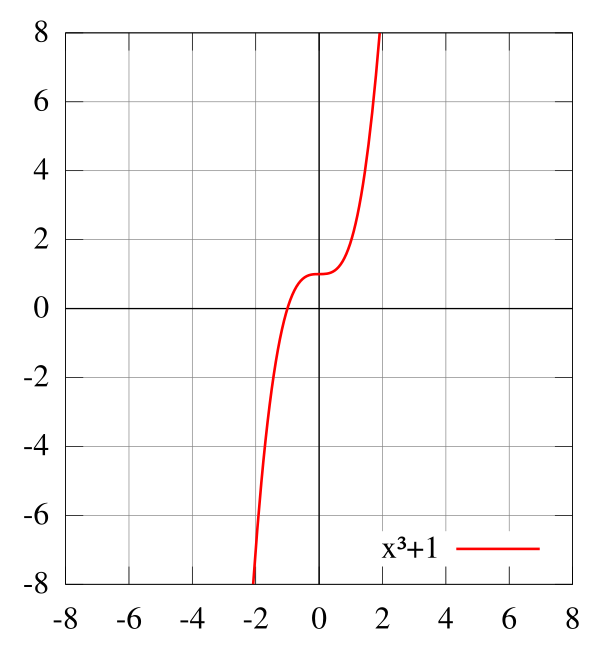
Существует множество функций, не подпадающих ни под определение чётных, ни под определение нечётных. Так, к таким относится функция ${\displaystyle y=x^{2}+5x-2}$.