Дуга окружности

Перейти к материалам ОГЭ/ЕГЭ

РУВИКИ для ОГЭ/ЕГЭ

        Читайте краткую версию статьи для подготовки к ОГЭ и ЕГЭ

Перейти

Дуга окружности с центральным углом

\alpha

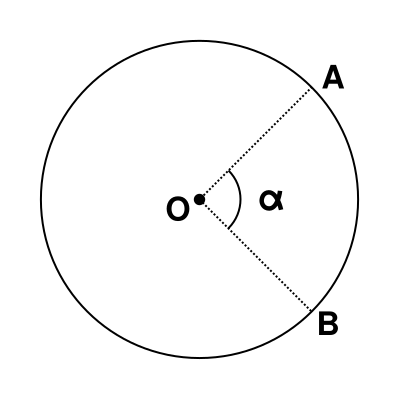
Дуга́ окру́жности (обозначается: ◡) — одна из двух частей (подмножеств) окружности, на которые её разбивают две различные принадлежащие ей точки. Любые две различные точки A и B окружности разбивают её на две части; каждая из этих частей называется дугой.

Если A и B — концы диаметра (то есть центральный угол AOB — развернутый), точка O — центр окружности, то они определяют две равные дуги, называемые полуокружностями. Если угол AOB не развернутый, то одна из двух дуг AB — это часть окружности, лежащая внутри угла AOB; говорят, что она меньше полуокружности, и что вторая дуга больше полуокружности. Эти углы и дуги называют дополнительными.

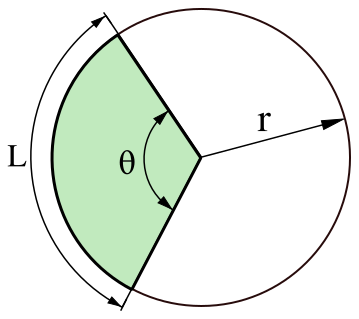
Дуги можно измерять в угловых единицах (например, в градусах или радианах), однако равные по центральным углам дуги разных окружностей не обязательно равны по длине — их длины прямо пропорциональны радиусу окружности, так что они равны только при равенстве радиусов.

Свойства

L

— дуга окружности

Длина дуги $L$ $L$ окружности радиуса $r$ $r$ вычисляется по формуле:
- $L=r\theta$ ; где $\theta$ — центральный угол, выраженный в радианах;
- $L=\pi r{\frac {a^{\circ }}{\displaystyle {180^{\circ }}}}$ ; где $a^{\circ }$ — центральный угол, выраженный в градусах.
Длина хорды $m$ $m$ , стягивающей дугу окружности радиуса $r$ $r$ с центральным углом $\theta$ $\theta$ :
- $m=2r\sin {\frac {\theta }{2}}=2{\frac {L}{\theta }}\sin {\frac {\theta }{2}}.$

Вариации и обобщения

В более широком смысле понятие «дуга» (простая дуга, жорданова дуга) может означать часть произвольной кривой, заключённую между двумя её точками и не содержащую точек самопересечения^[1].

См. также

Примечания

↑ Дуга // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2. — С. 391. — 1104 с.

Ссылки

«Углы, градусы и радианы» — перевод статьи Intuitive Guide to Angles, Degrees and Radians | BetterExplained (англ.)

[1] Дуга // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2. — С. 391. — 1104 с.

[1]