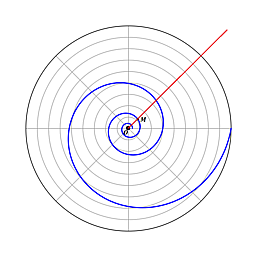
Логарифмическая спираль

Экспертиза РАН

Проводится экспертиза
Российской академией наук

Подробнее

Экспертиза РАН

Проводится экспертиза
Российской академией наук

Подробнее

Логарифмическая спираль
Область использования	Математика

Логарифми́ческая спира́ль или изогональная спираль — плоская трансцендентная кривая.

История

Спираль логарифмическая впервые упоминается в письме Декарта к Мерсенну (1638). Независимо от Декарта ее открыл Торричелли (1644). Особое внимание изучению свойств этой кривой уделял Я. Бернулли (1692), называвший ее spira mirabilis — «дивная спираль». Открытые им свойства инвариантности кривой относительно различных преобразований настолько поразили его, что он склонен был приписывать мистический смысл этой кривой и пожелал иметь на своей могиле изображение spira mirabilis с надписью “Eadem mutata resurgo” — «Изменённая воскресаю прежней». Так как при перемножении и показатели складываются, то оказывается, что кривая имеет свойства, роднящие ее с логарифмами. Поэтому Вариньон (1704) предложил назвать кривую логарифмической спиралью. Однако, по-видимому, это название употреблялось и раньше, в переписке.

Позднее логарифмическая спираль была предметом многочисленных исследований. Так, её кинематическое свойство найдено Э. Каталаном (1856).

Надгробие Бернулли

Якоб Бернулли хотел, чтобы на его могиле была выгравирована логарифмическая спираль, но вместо этого по ошибке на его надгробие поместили архимедову спираль. Тем не менее, надпись на латыни, выгравированная согласно завещанию вокруг спирали, «EADEM MUTATA RESURGO», свидетельствует о том, что имеется в виду именно логарифмическая спираль, которая обладает замечательным свойством восстанавливать свою форму после различных преобразований.

Определение

Пусть луч равномерно вращается около неподвижной точки $O$ (полюс) с постоянной угловой скоростью $\omega$, а точка $M$ движется вдоль луча, удаляясь от $O$ со скоростью, пропорциональной расстоянию $OM$ (Рис.1 ). Линия, описываемая точкой, называется логарифмической спиралью.

Рис. 1.

Уравнение в полярных координатах

Уравнение кривой $r=ae^{m\theta }$, где $\theta$ — угол отклонения точки от нуля, $r$ — радиус-вектор точки, $a$ — коэффициент, отвечающий за радиус витков, $m$ — коэффициент, отвечающий за расстояние между витками, $e$ — число Эйлера.

В параметрической форме может быть записана как

$x(t)=r\cos t=ae^{mt}\cos t\,,$

$y(t)=r\sin t=ae^{mt}\sin t\,,$

где $a,m$ — действительные числа, $t$ — аналог $\theta$ в выражении в полярных координатах.

Свойства

• Так как производная $r'_{\theta }=mae^{m\theta }$, так что $\operatorname {tg} \omega ={\frac {1}{m}}={\text{const}}$, и сам угол $\omega ={\text{const}}$. Таким образом, логарифмическая спираль обладает свойством, что угол между радиусом-вектором и касательной сохраняет постоянную величину. Иными словами, логарифмическая спираль пересекает все свои радиусы-векторы под постоянным углом.
• Свойством, описанным выше, логарифмическая спираль напоминает окружность, которая также пересекает радиусы-векторы, исходящие из центра, под постоянным (под прямым) углом. В этом смысле окружность можно рассматривать как частный случай логарифмической спирали, отвечающий $m=0$ .

• Производная функции $\mathbf {r} '(\vartheta )$ пропорциональна параметру m. Другими словами, он определяет, насколько плотно и в каком направлении закручивается спираль. В предельном случае, когда m = 0 $(\varphi =\pi /2)$ спираль вырождается в окружность радиуса a. Наоборот, когда m стремится к бесконечности $(\varphi \rightarrow 0),$ спираль стремится к прямой линии. Угол, дополняющий $\varphi$ до 90°, называется наклоном спирали.
• Когда угол $\theta$ растёт от $0$ до $+\infty$, точка делает бесчисленное множество оборотов вокруг полюса, быстро удаляясь от него в бесконечность; расстояния между витками уже не равны. Угол $\theta$ может принимать и отрицательные значения; когда $\theta$ стремится к $-\infty$, то радиус-вектор $r$ стремится к $0$. Кривая бесконечное множество раз заворачивается вокруг полюса, безгранично к нему приближаясь (но никогда не достигая); полюс является асимптотической точкой кривой.
• Поворачивая полярную ось вокруг полюса, можно добиться уничтожения множителя $a$ и привести уравнение логарифмической спирали к простейшему виду: $r=e^{m\theta }$.
• Если угол $\theta$ возрастает (или убывает) в арифметической прогрессии, то $r$ возрастает (убывает) в геометрической прогрессии.
• Радиус кривизны в каждой точке спирали пропорционален длине дуги спирали от её начала до этой точки.

Интересные факты

• 

  a=0.01, b=0.15

• 

  a=1, b=0.15

• 

  a=1000, m=0.15

• 

  Раковина моллюска по форме близка к логарифмической спирали

• 

  Область низкого давления над Исландией

• 

  Спиральная галактика Водоворот

Обобщение

Логарифмическая спираль есть Синусоидальная спираль при $n\to 1$;

Примечания

Литература

• Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. Изд. 3-е, испр. — М.: Издательство ЛКИ, 2008. — 248 с.
• Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, Главная редакция физико-математической литературы, 1981. — 720 с.
• Выгодский М. Я. Справочник по высшей математике. — М.: АСТ: Астрель, 2006. — 991 с.
• Соколов Д. Д. Логарифмическая спираль// Математическая энциклопедия (в 5 томах) / Гл. ред. И. М. Виноградов. — М.: Советская Энциклопедия, 1984. — Т. 3. — С. 406. — 1184 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: Наука, Главная редакция физико-математической литературы, 1970. — Т. 1. — 616 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: Наука, Главная редакция физико-математической литературы, 1970. — Т. 2. — 800 с.