Действительные числа

Действи́тельное (вещественное) число — это число, которое может принимать любое значение на числовой прямой, включая рациональные и иррациональные числа. Действительные числа используются для измерения непрерывных величин и являются фундаментальным понятием в математике^[1].

Основные понятия

Натуральные числа — числа, используемые при счёте предметов: 1, 2, 3, и так далее. Ноль не является натуральным числом.
Целые числа — натуральные числа, их отрицания и ноль.
Рациональные числа — числа, представимые в виде дроби ${\dfrac {p}{q}}$ , где $p$ — целое число, а $q$ — натуральное число. Их десятичное представление конечное или периодическое.
Иррациональные числа — числа, не представимые в виде обыкновенной дроби, но их можно записать в виде бесконечной непериодической дроби: ${\sqrt {2}}$ , $\pi$ , $e$ .
Действительные (вещественные) числа— объединение рациональных и иррациональных чисел^[2].

Обозначение числовых множеств

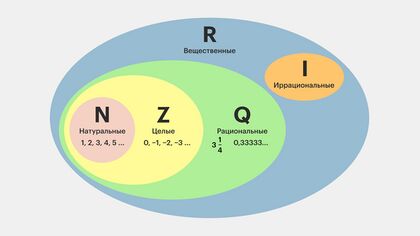
Изображение числовых множеств с помощью диаграммы Эйлера-Венна

Числовые множества принято обозначать следующими буквами:

$\mathbb {N}$ — множество натуральных чисел: $\mathbb {N} =\left\{1,2,3,...\right\}$ ;

$\mathbb {Z}$ — множество целых чисел: $\mathbb {Z} =\left\{...-2,-1,0,1,2,...\right\}$ ;

$\mathbb {Q}$ — множество рациональных чисел: $\mathbb {Q} =\left\{{\frac {p}{q}}|p\in Z,q\in N\right\}$ ;

$\mathbb {I}$ — множество иррациональных чисел;

$\mathbb {R}$ — множество действительных чисел.

Свойства действительных чисел

Упорядоченность

Действительные числа можно сравнивать: для любых $a$ и $b$ верно одно из соотношений $a<b$ , $a=b$ или $a>b$ .

Непрерывность

Между любыми двумя различными действительными числами всегда существует другое действительное число. Это означает, что числовая прямая непрерывна без «пробелов».

Поле действительных чисел

Действительные числа образуют поле, в котором определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), удовлетворяющие определённым аксиомам (коммутативность, ассоциативность, существование единицы и нуля и т. д.).

Представление действительных чисел

Понятие действительного числа является одним из основных в математике. Оно может быть представлено тремя методами. В школьной программе принято введение действительных чисел методом бесконечных десятичных дробей.

Десятичное разложение

Любое действительное число можно записать в виде десятичной дроби.

Рациональные числа:

 ${\dfrac {1}{2}}=0{,}5$ ; 
 ${\dfrac {1}{3}}=0{,}333\ldots =0,(3)$ .

Иррациональные числа:

 Любое число вида  ${\sqrt {p}}$ , где  $p$  — простое число ( ${\sqrt {2}},{\sqrt {3}},{\sqrt {5}}$  и т.д.):  ${\sqrt {2}}\approx 1,41421356...$ ; число  $\pi$  — отношение длины окружности к её радиусу:  $\pi \approx 3,14159...$  .

Геометрическое представление

Каждому действительному числу соответствует точка на числовой прямой, и каждой точке на этой прямой — действительное число. Изображение действительного числа — точка $M$ — называется координатой точки. Числовая прямая называется также координатной прямой.

Координатная прямая с точкой М

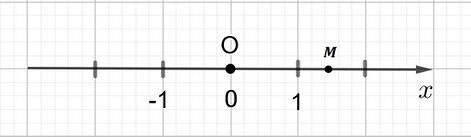
Множество действительных чисел $\mathbb {R}$ обозначается также $(-\infty ;+\infty )$ ^[3].

Применение действительных чисел

Математический анализ: изучение пределов, непрерывности, производных и интегралов.
Геометрия: измерение длин, площадей и объёмов.
Физика: описание непрерывных процессов и величин, таких как время, скорость и энергия.
Инженерные науки: расчёты в строительстве, электронике и других технических областях.

Заключение

Действительные числа являются основой для большинства разделов математики и её приложений. Они позволяют описывать и анализировать непрерывные процессы и величины, что необходимо для понимания и решения разнообразных задач в науке и технике.

Примечания

↑ Никольский С.М., Потапов М. К., Решетников Н. Н., Шевкин А. В. Алгебра. 7 класс: учебник для общеобразовательных организаций. — М.: Просвещение, 2021. — С. 30. — 294 с.
↑ Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Математика. Алгебра : 7-й класс : базовый уровень : учебник / под ред. С. А. Теляковского. — М.: Просвещение, 2024. — С. 9. — 255 с.
↑ Кожухов И.Б., Прокофьев А.А. Математика. Полный справочник. — М., 2008. — С. 48—49. — 352 с.

Литература

Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Учебник «Алгебра 7 класс. Учебник для общеобразовательных учреждений» (рус.). — 2013.
Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Учебник «Алгебра 8 класс. Базовый уровень» (рус.). — 2023.
Дорофеев Г. В., Суворова С. Б., Бунимович Е. А., Кузнецова Л. В., Минаева С. С., Рослова Л. О. Учебник «Алгебра. 9 класс» (рус.). — 2014.

[1] Никольский С.М., Потапов М. К., Решетников Н. Н., Шевкин А. В. Алгебра. 7 класс: учебник для общеобразовательных организаций. — М.: Просвещение, 2021. — С. 30. — 294 с.

[2] Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Математика. Алгебра : 7-й класс : базовый уровень : учебник / под ред. С. А. Теляковского. — М.: Просвещение, 2024. — С. 9. — 255 с.

[3] Кожухов И.Б., Прокофьев А.А. Математика. Полный справочник. — М., 2008. — С. 48—49. — 352 с.

[1]

[2]

[3]