Формула Пика

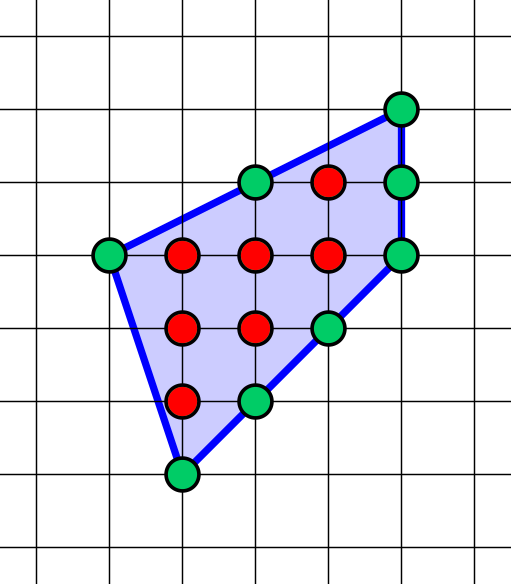
Площадь многоугольника с целочисленными вершинами^[1] равна ${\displaystyle {\text{В}}+{\dfrac {\text{Г}}{2}}-1}$, где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

• Площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2.
  • Этот факт даёт геометрическое доказательство формулы для разности подходящих дробей цепной дроби.

• Многочлен Эрара даёт один из вариантов обобщения формулы Пика на старшие размерности.

• Если все грани целочисленного многогранника ${\displaystyle M}$ центрально симметричны (в частности если многогранник является зонэдром) то его объём может быть вычислен по формуле

  ${\displaystyle V(M)={\tfrac {1}{4\pi }}\cdot \sum _{v}\alpha (v),}$

где суммирование ведётся по всем целочисленным точкам ${\displaystyle v\in M}$ и ${\displaystyle \alpha (v)}$ телесный угол ${\displaystyle M}$ при ${\displaystyle v}$; если ${\displaystyle v}$ лежит внутри ${\displaystyle M}$, то считается что ${\displaystyle \alpha (v)=4\cdot \pi }$.^[2]

• Аналогичное утверждение верно и в ${\displaystyle n}$-мерном евклидовом пространстве ${\displaystyle \mathbb {E} ^{n}}$

${\displaystyle V(M)={\tfrac {1}{\omega _{n}}}\cdot \sum _{v}\alpha (v),}$

где ${\displaystyle \omega _{n}}$ обозначает площадь единичной сферы в ${\displaystyle \mathbb {E} ^{n}}$.