Поверхность

Древние математики почти не рассматривали поверхностей, кроме плоскости, шара и некоторых поверхностей вращения (параболоида, эллипсоида, двуполосного гиперболоида). Они исследовали только части этих поверхностей с целью определения их площадей. Ферма сделал попытку ввести в теорию поверхностей, рассматриваемых как геометрические места, общую точку зрения. К этому же времени относятся отдельные эпизодические результаты: Рен (1669) и Паран (1702) установили, что однополосный гиперболоид — линейчатая поверхность. Паран (1705) вывел уравнение общей шаровой поверхности. С 1700 года, после исследования Парана, считается общепризнанным, что ${\displaystyle z=f(x,y)}$ — уравнение поверхности. Клеро считал очевидным, что уравнение между ${\displaystyle x,\,y,\,z}$ определяет поверхность. Лагир (1679), а затем Клеро (1731) вывели уравнения поверхностей вращения, в частности уравнения конуса, эллипсоида и однополосного гиперболоида. Параметрическое представление поверхности встречается у Эйлера (1766) и в картографических работах Лагранжа. Систематически оно использовалось Гауссом (с 1822).

Неизвестно, когда в математике появились конус и пирамида. Вавилонские математики знали усечённый конус вращения, усечённую пирамиду. Эллипсоиды, двуполостный гиперболоид и параболоид вращения рассматривались впервые Архимедом в трактате «О сфероидах и коноидах». Он нашёл объём шара и площадь поверхности сферы. Валлис в своём сочинении о конических сечениях рассмотрел эллипсоиды, эллиптические параболоиды общего вида (1655), а затем — однополосный гиперболоид вращения, названный им «цилиндроид» (1670). Рен в это же время рассмотрел линейчатые поверхности.

В 1728 году Эйлер рассмотрел цилиндрические, конические поверхности общего вида и поверхности вращения. Впервые поверхности второго порядка, представленные уравнениями второй степени, стали широко известными после работы Эйлера «Введение в анализ бесконечных» (1748). Начиная с этой работы, в классификации поверхностей повторяется выражение, составленное из коэффициентов уравнения поверхности. Основным методом исследования формы поверхности у Эйлера было преобразование системы координат и приведение уравнения к каноническому виду. Этим же путём следовал Монж, в работах которого только в начале XIX века появились современные названия невырожденных поверхностей второго порядка (1801). Исследование поверхностей методом сечений ввёл Коши, хотя Ферма уже рассматривал сечение поверхности координатными плоскостями как характеризующие поверхность.

Для восстановления взаимной однозначности конформного отображения Риман создал новый образ — многолистную поверхность (1851). Позже идеи Римана были разъяснены и в более доступной форме изложены его учениками. В учебники понятие поверхности Римана вошло через 20 лет (1874).

Поверхности, на которых некоторая функция имеет постоянное значение, впервые встречаются у Маклорена (1742) и Клеро (1743). Ламе в статьях 1834—1837 гг. рассмотрел не только поверхности уровня, но и производную по нормали к поверхности, установил величину наибольшей скорости роста функции, таким образом, в его изложении не хватало только векторных величин, чтобы оно было вполне современным. Результаты Ламе, переведённые на векторный язык Максвеллом (1873), полностью вошли в современные учебники^[2].

В элементарной геометрии рассматриваются плоскости, многогранные поверхности, а также некоторые кривые поверхности (например, сфера). Каждая из кривых поверхности определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, поверхность шара — множество точек, находящихся на заданном расстоянии от данной точки (центра шара). Понятие поверхности лишь поясняется, а не определяется. Например, говорят, что поверхность есть граница тела или след движущейся линии.

Математически строгое определение поверхности основывается на понятиях топологии. С точки зрения топологии поверхность является двумерным многообразием^[3]. Основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям или изгибаниям). Более точно простой поверхностью называется образ гомеоморфного (то есть взаимно однозначного и взаимно непрерывного) отображения внутренности квадрата. Этому определению можно дать аналитическое выражение. Пусть на плоскости с прямоугольной системой координат ${\displaystyle u}$ и ${\displaystyle v}$ задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам ${\displaystyle 0<u<1}$, ${\displaystyle 0<v<1}$. Гомеоморфный образ этого квадрата в пространстве с прямоугольной системой координат ${\displaystyle x,\,y,\,z}$ задаётся при помощи формул ${\displaystyle x=\varphi (u,v)}$, ${\displaystyle y=\psi (u,v)}$, ${\displaystyle z=\chi (u,v)}$ (параметрические уравнения поверхности). При этом от функций ${\displaystyle \varphi (u,v)}$, ${\displaystyle \psi (u,v)}$, ${\displaystyle \chi (u,v)}$ требуется, чтобы они были непрерывными и чтобы для различных точек ${\displaystyle (u,v)}$ и ${\displaystyle (u',v')}$ были различны соответствующие точки ${\displaystyle (x,y,z)}$ и ${\displaystyle (x',y',z')}$. Примером простой поверхности является полусфера. Вся же сфера не является простой поверхностью. Это вызывает необходимость дальнейшего обобщения понятия поверхности.

В трёхмерном евклидовом пространстве ${\displaystyle \mathbb {E} ^{3}}$ поверхность понимается как связное множество простых поверхностей. Обычно поверхность в ${\displaystyle \mathbb {E} ^{3}}$ задаётся вектор-функцией ${\displaystyle \mathbf {r} =\mathbf {r} (x(u,v),y(u,v),z(u,v))}$, где ${\displaystyle 0\leqslant u\leqslant 1}$, ${\displaystyle 0\leqslant v\leqslant 1}$, а ${\displaystyle x=x(u,v),y=y(u,v),z=z(u,v)}$ — функции параметров ${\displaystyle u}$ и ${\displaystyle v}$, удовлетворяющие некоторым условиям регулярности^[3].

В дифференциальной геометрии исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, то есть существования в каждой точке поверхности определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции ${\displaystyle \varphi (u,v)}$, ${\displaystyle \psi (u,v)}$, ${\displaystyle \chi (u,v)}$ предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. Кроме того, требуется, чтобы в каждой точке хотя бы один из определителей ${\displaystyle {\begin{vmatrix}\varphi '_{u}&\varphi '_{v}\\\psi '_{u}&\psi '_{v}\end{vmatrix}}}$, ${\displaystyle {\begin{vmatrix}\varphi '_{u}&\varphi '_{v}\\\chi '_{u}&\chi '_{v}\end{vmatrix}}}$, ${\displaystyle {\begin{vmatrix}\psi '_{u}&\psi '_{v}\\\chi '_{u}&\chi '_{v}\end{vmatrix}}}$ был отличен от нуля.

Поверхность определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений ${\displaystyle \Phi (x,\,y,\,z)=0}$. Определённая таким образом поверхность может и не иметь наглядного геометрического образа. В этом случае для сохранения общности говорят о мнимых поверхностях. Например, уравнение ${\displaystyle x^{2}+y^{2}+z^{2}+1=0}$ определяет мнимую сферу, хотя в действительном пространстве нет ни одной точки, координаты которой удовлетворяют этому уравнению^[1].

• В топологии, поверхность, окрестность каждой точки которой есть простая поверхность, называется правильной.
• В аналитической геометрии правильная поверхность определяется следующим образом:

Если функция ${\displaystyle \Phi (x,\,y,\,z)}$ непрерывна в некоторой точке и имеет в ней непрерывные частные производные ${\displaystyle {\frac {\partial \Phi }{\partial x}},{\frac {\partial \Phi }{\partial y}},{\frac {\partial \Phi }{\partial z}}}$ , по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением ${\displaystyle \Phi (x,\,y,\,z)=0}$, будет правильной поверхностью.

С точки зрения топологического строения поверхности, как двумерные многообразия, разделяются на несколько типов:

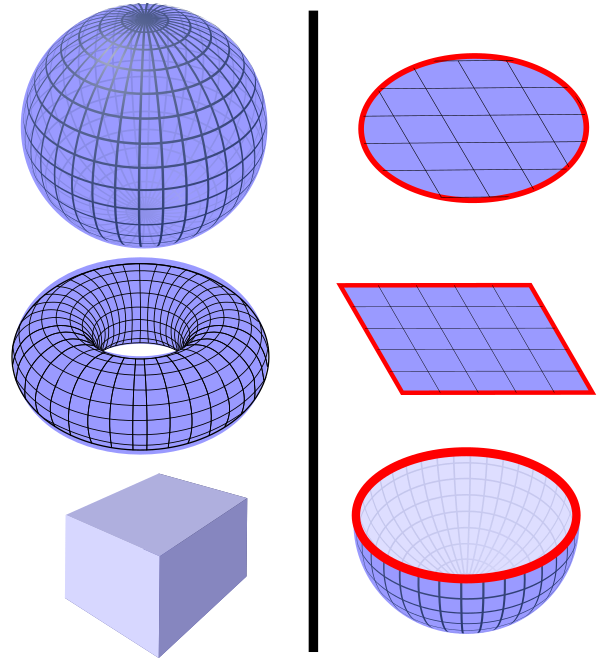
• замкнутые и открытые поверхности;
• ориентируемые и неориентируемые поверхности^[1].

Поверхность с трёхмерном пространстве можно определить следующим образом:

• в явной форме ${\displaystyle z=z(x,y)}$;
• в явной форме ${\displaystyle F(x,y,z)=0}$;
• в параметрической форме ${\displaystyle x=x(u,v),y=y(u,v),z=z(u,v)}$;
• в векторной форме ${\displaystyle \mathbf {r} =\mathbf {r} (u,\ v)}$, где ${\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k} }$ означает радиус-вектор точки поверхности ${\displaystyle M(x,y,z)}$: ${\displaystyle \mathbf {r} (u,\ v)=x(u,\ v)\mathbf {i} +y(u,\ v)\mathbf {j} +z(u,\ v)\mathbf {k} }$^[4].

Теория поверхностей является разделом дифференциальной геометрии. В классической теории поверхностей изучаются свойства поверхностей, не меняющихся при их движении, при любых изометрических преобразованиях всего пространства, поэтому они относятся к так называемой метрической теории поверхностей. Одна из основных задач теории — измерения на поверхности — возникла в геодезии, то есть связана с измерениями на поверхности Земли. Совокупность параметров, связанных с измерениями на поверхности, составляет внутреннюю геометрию поверхности. К внутренней геометрии поверхностей относятся такие понятия, как длина линии, угол между двумя направлениями, площадь области, а также геодезические линии, геодезическая кривизна линии и многое другое.

Внутреннюю геометрию определяет первая квадратичная форма поверхности ${\displaystyle ds^{2}=E\,du^{2}+2F\,du\,dv+G\,dv^{2}}$, где ${\displaystyle E=(r_{u},r_{u});F=(r_{u},r_{v});G=(r_{v})(r_{v})}$, ${\displaystyle r_{u}={\frac {\partial r}{\partial u}},r_{v}={\frac {\partial r}{\partial v}}}$, ${\displaystyle r=r(u,v)}$- радиус-вектор точки поверхности, ${\displaystyle u,v}$ — её криволинейные координаты, (⋅,⋅) означает скалярное произведение, выражающая квадрат дифференциала дуги линии на поверхности.

Если известны функции ${\displaystyle E=E(u,v)}$, ${\displaystyle F=F(u,v)}$, ${\displaystyle G=G(u,v)}$, то, зная внутренние уравнения линии ${\displaystyle u=u(t)}$, ${\displaystyle v=v(t)}$ и интегрируя ${\displaystyle ds}$, можно определить длину этой линии. Существуют формулы, которые при данных ${\displaystyle E,F,G}$ выражают угол между двумя линиями и площадь области по внутренним уравнениям этих линий и по внутреннему уравнению контура области.

Изучение пространственного строения окрестности точки на поверхности производится при помощи второй квадратичной формы поверхности ${\displaystyle 2h=L\,du^{2}+2M\,du\,dv+N\,dv^{2}}$, где ${\displaystyle L=(r_{uu},n);M=(r_{uv},n);N=(r_{vv},n)}$, ${\displaystyle n={\frac {[r_{u},r_{v}]}{|[r_{u},r_{v}]|}}}$ — единичный вектор нормали к поверхности, [⋅,⋅] означает векторное произведение^[5].

Первая квадратичная форма представляет собой двумерный вариант метрики поверхности. Для регулярной поверхности её дискриминант ${\displaystyle EG-F^{2}>0}$ во всех точках. Коэффициент ${\displaystyle F=0}$ в точке поверхности тогда и только тогда, когда в этой точке координатные кривые ортогональны. В частности, на плоскости с декартовыми координатами ${\displaystyle u,\ v}$ получается метрика ${\displaystyle ds^{2}=du^{2}+dv^{2}}$ (теорема Пифагора).

Метрика не определяет однозначно форму поверхности. Например, метрики геликоида и катеноида, параметризованных соответствующим образом, совпадают, то есть между их областями существует соответствие, сохраняющее все длины (изометрия).

Метрические коэффициенты ${\displaystyle E,\ F,\ G}$ определяют не только длины всех кривых, но и вообще результаты всех измерений внутри поверхности (углы, площади, кривизна и др.). Поэтому всё, что зависит только от метрики, относится к внутренней геометрии.

Касательная плоскость есть плоскость, содержащая касательные ко всем гладким кривым, проходящим через эту точку.

Пусть гладкая кривая на параметрически заданной поверхности ${\displaystyle \mathbf {r} =\mathbf {r} (u,\ v)}$ задана в виде:

${\displaystyle u=u(t);\ v=v(t)}$.

Направление ${\displaystyle \mathbf {v} }$ касательной к такой кривой даёт вектор:

${\displaystyle \mathbf {v} ={\frac {d\mathbf {r} }{dt}}={\frac {\partial \mathbf {r} }{\partial u}}{\frac {du}{dt}}+{\frac {\partial \mathbf {r} }{\partial v}}{\frac {dv}{dt}}}$.

Отсюда видно, что все касательные ко всем кривым в данной точке лежат в одной плоскости, содержащей векторы ${\displaystyle {\frac {\partial \mathbf {r} }{\partial u}},{\frac {\partial \mathbf {r} }{\partial v}}}$, которые мы выше предположили независимыми.

Уравнение касательной плоскости в точке ${\displaystyle \mathbf {r_{0}} =(x_{0},y_{0},z_{0})}$ имеет вид:

${\displaystyle \left(\mathbf {r} -\mathbf {r_{0}} ,{\frac {\partial \mathbf {r} }{\partial u}},{\frac {\partial \mathbf {r} }{\partial v}}\right)=0\quad }$ (смешанное произведение векторов).

В координатах уравнения касательной плоскости для разных способов задания поверхности приведены в таблице:

	Касательная плоскость к поверхности в точке ${\displaystyle (x_{0},y_{0},z_{0})}$
Неявное задание	${\displaystyle {\frac {\partial F}{\partial x}}(x-x_{0})+{\frac {\partial F}{\partial y}}(y-y_{0})+{\frac {\partial F}{\partial z}}(z-z_{0})=0}$
Явное задание	${\displaystyle {\frac {\partial f}{\partial x}}(x-x_{0})+{\frac {\partial f}{\partial y}}(y-y_{0})=(z-z_{0})}$
Параметрическое задание	${\displaystyle {\begin{vmatrix}x-x_{0}&y-y_{0}&z-z_{0}\\x_{u}'&y_{u}'&z_{u}'\\x_{v}'&y_{v}'&z_{v}'\end{vmatrix}}=0}$

Все производные берутся в точке ${\displaystyle (x_{0},y_{0},z_{0})}$.

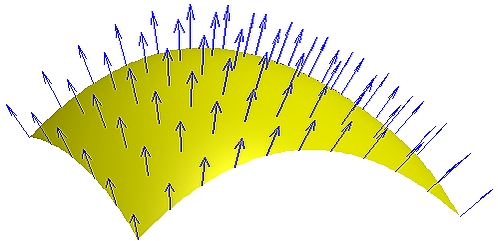
Одной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:

${\displaystyle n={\frac {[r_{u},r_{v}]}{|[r_{u},r_{v}]|}}}$.

Пусть ${\displaystyle M}$ — некоторая точка на поверхности ${\displaystyle S}$ и ${\displaystyle n}$ — единичный вектор нормали к поверхности в ${\displaystyle M}$. Линия ${\displaystyle L}$ пересечения ${\displaystyle S}$ с плоскостью, проходящей через ${\displaystyle n}$ в направлении ${\displaystyle dr=r_{u}du+r_{v}dv}$, называется нормальным сечением в этом направлении, а её кривизна — нормальной кривизной. Нормальная кривизна ${\displaystyle 1/R}$ вычисляется по формуле ${\displaystyle {\frac {1}{R}}={\frac {Ldu^{2}+2Mdudv+Ndv^{2}}{Edu^{2}+2Fdudv+Gdv^{2}}}}$.

Экстремальные значения нормальной кривизны в данной точке называются главными кривизнами, а соответствующие направления на поверхности — главными направлениями. Если главные кривизны в точке ${\displaystyle M}$ различны, то в этой точке существуют два главных направления. Линии, направления которых в каждой точке являются главными, называются линиями кривизны. Направления, в которых нормальная кривизна равна нулю, называются асимптотическими, а линии, имеющие в каждой точке асимптотическое направление, — асимптотическими линиями. Дальнейшее изучение свойств произвольных линий на поверхности (в первую очередь кривизн линий) тесно связано с кривизнами нормальных сечений. Кривизна в данной точке произвольной линии на поверхности может быть вычислена через кривизну нормального сечения с помощью формулы Мёнье, а кривизна произвольного нормального сечения в данной точке связана простым соотношением (формулой Эйлера) с главными кривизнами.

Поверхности, между точками которых можно установить такое взаимно однозначное соответствие, что длины соответствующих линий равны, называются изометричными. Изометричные поверхности имеют одинаковую геометрию, но их пространственное строение может быть различным и главные кривизны в соответствующих точках у них могут быть также различными. Однако произведение ${\displaystyle K}$ главных кривизн ${\displaystyle \kappa _{1}}$​ и ${\displaystyle \kappa _{2}}$​ не меняется при изометричных преобразованиях поверхности (теорема Гаусса, 1827) и поэтому может служить внутренней мерой искривлённости поверхности в данной точке. Величина ${\displaystyle K}$ называется полной или гауссовой кривизной поверхности в точке ${\displaystyle M}$ и выражается формулой ${\displaystyle K={\frac {LN-M^{2}}{EG-F^{2}}}}$. Полная кривизна в соответствии с теоремой Гаусса может быть выражена только через коэффициенты первой квадратичной формы и их производные.

Важное значение в теории поверхностей имеет вопрос о возможности изгибания поверхности, который можно сформулировать следующим образом: можно ли включить данную регулярную поверхность в однопараметрическое семейство изометричных неконгруэнтных регулярных поверхностей? При этом рассматриваются как сама возможность изгибания, так и изгибания специального вида. Задача изгибания поверхностей тесно связана с задачей определения поверхности по заданным основным квадратичным формам. Поскольку значение полной кривизны ${\displaystyle K}$ поверхности может быть выражено через коэффициенты первой квадратичной формы, то уравнение ${\displaystyle K={\frac {LN-M^{2}}{EG-F^{2}}}}$ является одним из соотношений, связывающих коэффициенты первой и второй форм. Другие два соотношения ${\displaystyle {\begin{matrix}{\frac {\partial \Delta }{\partial v}}-{\frac {\partial \Delta '}{\partial u}}+\Gamma _{22}^{2}\Delta -2\Gamma _{12}^{2}\Delta '+\Gamma _{11}^{2}\Delta ''=0,\\{\frac {\partial \Delta ''}{\partial u}}-{\frac {\partial \Delta '}{\partial v}}+\Gamma _{22}^{1}\Delta -2\Gamma _{12}^{1}\Delta '+\Gamma _{11}^{1}\Delta ''=0\end{matrix}}}$, где ${\displaystyle \Delta ={\frac {L}{\sqrt {EG-F^{2}}}}}$, ${\displaystyle \Delta '={\frac {M}{\sqrt {EG-F^{2}}}}}$, ${\displaystyle \Delta ''={\frac {N}{\sqrt {EG-F^{2}}}}}$, ${\displaystyle \Gamma _{jk}^{i}}$— символы Кристоффеля второго рода — были установлены К. М. Петерсоном (1853). Справедливо и обратное утверждение: если коэффициенты двух форм, одна из которых положительно определённая, удовлетворяют приведённым выше уравнениям, то существует определённая с точностью до движения и зеркального отражения поверхность, для которой указанные формы будут первой и второй квадратичными формами (теорема Бонне).

С начала двадцатого века в классической теории поверхностей появляется новое направление, в котором исследуется поверхность «в целом» по данным свойствам окрестностей её точек. Важные результаты в этой области получены Л. А. Люстерником и Л. Г. Шнирельманом, которыми утвердительно была решена проблема существования трёх замкнутых геодезических линий на регулярных замкнутых поверхностях, гомеоморфных сфере. Принципиально новые результаты были получены А. Д. Александровым и А. В. Погореловым в теории выпуклых поверхностей. Александров предложил новый метод исследования выпуклых поверхностей, основанный на приближении выпуклых поверхностей многогранниками. Н. В. Ефимов получил фундаментальные результаты по теории поверхностей отрицательной кривизны^[5].

Ещё один важный атрибут поверхности — её площадь, которая вычисляется по формуле:

${\displaystyle S=\iint \,|[\mathbf {r} '_{u}\times \mathbf {r} '_{v}]|\;\mathrm {d} \,u\,\mathrm {d} \,v}$.

Здесь ${\displaystyle \mathbf {r} '_{u}=\left\{{\frac {\partial x}{\partial u}},\,{\frac {\partial y}{\partial u}},\,{\frac {\partial z}{\partial u}}\right\},\ \mathbf {r} '_{v}=\left\{{\frac {\partial x}{\partial v}},\,{\frac {\partial y}{\partial v}},\,{\frac {\partial z}{\partial v}}\right\}}$.

В координатах получаем:

	Явное задание	Параметрическое задание
Выражение для площади	${\displaystyle \iint \,{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}\;\mathrm {d} \,x\,\mathrm {d} \,y}$	${\displaystyle \iint \,{\sqrt {\left({\frac {D(x,y)}{D(u,v)}}\right)^{2}+\left({\frac {D(y,z)}{D(u,v)}}\right)^{2}+\left({\frac {D(z,x)}{D(u,v)}}\right)^{2}}}\;\mathrm {d} \,u\,\mathrm {d} \,v}$

Площадь куска поверхности выражается следующими формулами^[6]:

• Общее выражение: ${\displaystyle S=\iint \limits _{D}{\frac {\operatorname {d} \!\sigma }{\cos \gamma }}}$, где область ${\displaystyle D}$ — проекция на плоскость ${\displaystyle XOY}$; в каждую точку области проецируется только одна точка поверхности; ${\displaystyle \gamma }$ — угол между касательной плоскостью и плоскостью ${\displaystyle XOY}$.
• В прямоугольных координатах: ${\displaystyle S=\iint {\sqrt {1+\left({\frac {\partial z}{\partial x}}\right)^{2}+\left({\frac {\partial z}{\partial y}}\right)^{2}}}\;\mathrm {d} \,x\,\mathrm {d} \,y}$.
• В полярных координатах: ${\displaystyle S=\iint {\sqrt {r^{2}+r^{2}\left({\frac {\partial z}{\partial \rho }}\right)^{2}+\left({\frac {\partial z}{\partial \varphi }}\right)^{2}}}\operatorname {d} \!r\operatorname {d} \!\varphi }$.

Кусок поверхности ${\displaystyle S}$, заданный в параметрической форме ${\displaystyle x=x(u,v),y=y(u,v),z=z(u,v)}$, где точка ${\displaystyle (u,v)}$ пробегает некоторую область ${\displaystyle G}$ плоскости ${\displaystyle u,v}$, называется гладким, если различные пары значений ${\displaystyle (u,v)}$ дают разные точки ${\displaystyle S}$, частные производные функций ${\displaystyle x(u,v),y(u,v),z(u,v)}$ непрерывны и ${\displaystyle {\mathsf {rang}}\left({{\frac {\partial x}{\partial u}}{\frac {\partial y}{\partial u}}{\frac {\partial z}{\partial u}} \atop {\frac {\partial x}{\partial v}}{\frac {\partial y}{\partial v}}{\frac {\partial z}{\partial v}}}\right)=2}$. Если поверхность ${\displaystyle S}$ состоит из конечного числа гладких кусков поверхности, то ${\displaystyle S}$ называется кусочно гладкой. Гладкая поверхность ${\displaystyle S}$ называется двусторонней, если в каждой точке поверхности можно выбрать нормаль так, что при обходе каждой замкнутой кривой, лежащей на ${\displaystyle S}$, возвращаются в исходную точку кривой с тем же направлением нормали. Стороны двусторонней поверхности могут быть охарактеризованы направлением соответствующих нормалей. В противном случае поверхность называют односторонней. Односторонней поверхностью является, например, лист или лента Мёбиуса (см. рис.).

Лента Мёбиуса

Всюду в дальнейшем под поверхностью понимается двусторонняя поверхность.

Пусть поверхность ${\displaystyle S}$ задана параметрически: ${\displaystyle x=x(u,v),y=y(u,v),z=z(u,v)}$, где точка ${\displaystyle (u,v)}$ пробегает некоторую область ${\displaystyle \Gamma }$ плоскости ${\displaystyle u,v}$. Тогда площадь ${\displaystyle \Delta S}$ поверхности определяется поверхностным интегралом ${\displaystyle \Delta S=\iint \limits _{(\Gamma )}{\sqrt {EG-F^{2}}}du\,dv}$, где ${\displaystyle E={\biggl (}{\frac {\partial x}{\partial u}}{\biggr )}^{2}+{\biggl (}{\frac {\partial y}{\partial u}}{\biggr )}^{2}+{\biggl (}{\frac {\partial z}{\partial u}}{\biggr )}^{2}}$, ${\displaystyle F={\frac {\partial x}{\partial u}}{\frac {\partial x}{\partial v}}+{\frac {\partial y}{\partial u}}{\frac {\partial y}{\partial v}}+{\frac {\partial z}{\partial u}}{\frac {\partial z}{\partial v}}}$, ${\displaystyle G={\biggl (}{\frac {\partial x}{\partial v}}{\biggr )}^{2}+{\biggl (}{\frac {\partial y}{\partial v}}{\biggr )}^{2}+{\biggl (}{\frac {\partial z}{\partial v}}{\biggr )}^{2}}$; подынтегральное выражение ${\displaystyle dS={\sqrt {EG-F^{2}}}du\,dv}$ называется элементом поверхности.

Если ${\displaystyle S}$ задана явно уравнением ${\displaystyle z=\varphi (x,y)}$, причём ${\displaystyle (x,y)}$ пробегает область ${\displaystyle S'}$ (проекцию области ${\displaystyle S}$ на плоскость ${\displaystyle xOy}$), то ${\displaystyle \Delta S=\iint \limits _{(S'')}{\sqrt {1+p^{2}+q^{2}}}dx\,dy}$, где ${\displaystyle p={\frac {\partial z}{\partial x}}}$, ${\displaystyle q={\frac {\partial z}{\partial y}}}$^[7].

Гладкие поверхности, для которых средняя кривизна равна 0, называются минимальными. Вопрос, существует ли минимальная поверхность с заданной границей, называется задачей Плато по имени бельгийского физика Жозефа Плато. Известно много примеров минимальных поверхностей, такие как катеноид, геликоид, поверхность Шерка и поверхность Эннепера.

Также важной характеристикой поверхности является её ориентация. Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным вектором нормали. Ориентированной называется двусторонняя поверхность с выбранным направлением нормали. Примерами односторонних и, следовательно, неориентируемых поверхностей являются бутылка Клейна или Лента Мёбиуса.

Цилиндрическая поверхность образуется прямой линией (образующей), перемежающейся параллельно заданному направлению вдоль некоторой кривой (направляющей). Тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, являющимися его основаниями, называется цилиндром.

• Круговой прямой цилиндр имеет в основании круг, и его образующие перпендикулярны к плоскости основания. Площадь полной поверхности такого цилиндра выражается формулой ${\displaystyle S=2\pi R(R+h)}$, где ${\displaystyle R}$ — радиус основания, ${\displaystyle h}$ — высота.
• Усечённый круговой цилиндр имеет площадь полной поверхности ${\displaystyle S=\pi R\left[h_{1}+h_{2}+R+{\sqrt {R^{2}+\left({\frac {h_{2}-h_{1}}{2}}\right)^{2}}}\right]}$.

Коническая поверхность образуется прямой линией (образующей), перемещающейся вдоль кривой линии (направляющей) и имеющей неподвижную точку (вершину). Тело, ограниченное конической поверхностью с замкнутой направляющей и плоскостью, образующей основание, называется конусом.

• Круговой прямой конус имеет в основании круг, и его высота проходит через центр круга. Площадь полной поверхности такого конуса выражается формулой ${\displaystyle S=\pi R(R+l)}$, где ${\displaystyle R}$ — радиус основания, ${\displaystyle l}$ — длина образующей^[8].

Если ${\displaystyle c\in W(f)}$, то точечное множество ${\displaystyle \{(x_{1},...,x_{n})|f(x_{1},...,x_{n})=c\}\subset {\mathsf {R}}^{n}}$ называется поверхностью уровня функции ${\displaystyle f}$. Таким образом, на поверхности уровня функция ${\displaystyle f}$ имеет постоянное значение. В случае ${\displaystyle n=2}$ это точечное множество называется линией уровня^[9].

Поверхность вращения может быть получена вращением кривой в плоскости xz вокруг оси z в предположении, что кривая не пересекает ось z. Предположим, что кривая задана выражением

${\displaystyle x=\varphi (t),\,\,z=\psi (t)}$

с t, лежащим в (a, b), и параметризованная длиной дуги, так что

${\displaystyle {\dot {\varphi }}^{2}+{\dot {\psi }}^{2}=1.}$

Тогда поверхность вращения является множеством точек

${\displaystyle M=\{(\varphi (t)\cos \theta ,\varphi (t)\sin \theta ,\psi (t))\colon t\in (a,b),\theta \in [0,2\pi )\}.}$

Гауссова кривизна и средняя кривизна задаются выражениями

${\displaystyle K=-{{\ddot {\varphi }} \over \varphi },\,\,K_{m}={-{\dot {\psi }}+\varphi ({\dot {\psi }}{\ddot {\varphi }}-{\ddot {\psi }}{\dot {\varphi }}) \over 2\varphi }.}$

Геодезические на поверхности вращения определяются отношением Клеро.

Поверхностями второго порядка в пространстве называются такие множества точек, координаты которых удовлетворяют уравнению вида

${\displaystyle a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{13}xz+2a_{23}yz+2a_{14}x+2a_{24}y+2a_{34}z+a_{44}=0}$;

в матричной форме: ${\displaystyle \mathbf {r} A\mathbf {r} ^{T}+2\mathbf {a} \mathbf {r} ^{T}+a_{44}=0}$, где ${\displaystyle \mathbf {r} =(x,y,z)}$, ${\displaystyle A={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}}$, ${\displaystyle \mathbf {a} =(a_{14},a_{24},a_{34})}$, ${\displaystyle (\mathbf {A} \neq 0)}$^[10].

Поверхность называется линейчатой, если она получается при движении в пространстве прямой (например, конус, цилиндр, однополостной гиперболоид, гиперболический параболоид). Если поверхность при этом может быть развёрнута на плоскость, то говорят о развёртывающейся поверхности (например, конус, цилиндр). Если пересечь поверхность плоскостью, приходящей через нормаль к поверхности в точке ${\displaystyle M}$, то образующаяся кривая называется нормальным сечением в точке ${\displaystyle M}$^[11].

Поверхности с постоянной отрицательной, нулевой и положительной кривизной Гаусса

Если поверхность имеет постоянную гауссову кривизну, она называется поверхностью постоянной кривизны.

• Единичная сфера в ${\displaystyle \mathbb {E} ^{3}}$ имеет постоянную гауссову кривизну +1.
• Евклидова плоскость и цилиндр имеют постоянную гауссову кривизну 0.
• Поверхность вращения с ${\displaystyle \varphi _{tt}=\varphi }$ имеет постоянную гауссову кривизну −1. Частный случай получается путём принятия ${\displaystyle \varphi (t)=C\mathrm {ch} \,t}$, ${\displaystyle C\mathrm {sh} \,t}$ и ${\displaystyle Ce^{t}}$. Последний случай является классической псевдосферой, образованной вращением трактрисы вокруг центральной оси. В 1868 году Эудженио Бельтрами показал, что геометрия псевдосферы была напрямую связана с геометрией гиперболической плоскости, открытой независимо Лобачевским (1830) и Бойяи (1832). Эта поверхность постоянной кривизны лучше понимается в терминах метрики Пуанкаре на верхней полуплоскости или единичном круге и может быть описана другими моделями, такими как модель Кляйна или гиперболоидная модель, полученная рассмотрением двулистного гиперболоида ${\displaystyle q(x,y,z)=-1}$ в трёхмерном пространстве Минковского, где ${\displaystyle q(x,y,z)=x^{2}+y^{2}-z^{2}}$. Каждая из этих поверхностей постоянной кривизны имеет транзитивную группу Ли симметрий.