Среднеквадратическое отклонение

В элементарной математике средним квадратичным отклонением называется квадратный корень из средних арифметических всех квадратов разностей между данными числами и их средним арифметическим: ${\displaystyle \sigma ={\sqrt {\frac {(a_{1}-m_{a})^{2}+...+(a_{n}-m_{a})^{2}}{n}}}}$, где ${\displaystyle a_{1},...,a_{n}}$ — данные числа, ${\displaystyle n}$ — их число, ${\displaystyle m_{a}}$ — их среднее арифметическое^[2].

В теории вероятностей средним квадратичным отклонением ${\displaystyle \sigma _{X}}$​ случайной величины ${\displaystyle X}$ называется арифметическое значение квадратного корня из её дисперсии^[3]: ${\displaystyle \sigma _{x}={\sqrt {d_{x}}}}$.

В математической статистике квадратичное отклонение употребляют как меру качества статистических оценок и называют в этом случае квадратичной ошибкой^[1].

Взвешенное квадратичное отклонение выражается формулой ${\displaystyle {\sqrt {\frac {p_{1}(x_{1}-a)^{2}+...+p_{n}(x_{n}-a)^{2}}{p_{1}+...+p_{n}}}}}$, где положительные числа ${\displaystyle p_{1},p_{2},...,p_{n}}$ называются весами, соответствующими величинам ${\displaystyle x_{1},x_{2},...,x_{n}}$. Взвешенное квадратичное отклонение достигает наименьшего значения при ${\displaystyle a}$, равном взвешенному среднему ${\displaystyle {\frac {p_{1}x_{1}+...+p_{n}x_{n}}{p_{1}+...+p_{n}}}}$. Наименьшее значение квадратичного отклонения достигается при ${\displaystyle a={\bar {x}}}$, где ${\displaystyle {\bar {x}}={\frac {(x_{1}+\ldots +x_{n})}{n}}}$ — среднее арифметическое величин ${\displaystyle x_{1},x_{2},...,x_{n}}$. В этом случае квадратичное отклонение может служить мерой рассеяния величин ${\displaystyle x_{1},x_{2},...,x_{n}}$^[1].

В математической статистике одной из центральных задач является оценивание теоретического распределения случайной величины на основе выборочных данных^[3].

Пусть произведена выборка объёма ${\displaystyle n}$. Выборочной средней ${\displaystyle {\bar {x}}_{B}}$ называют среднее арифметическое значений выборки. Для характеристики рассеивания выборочных значений относительно выборочной средней вводится понятие выборочной дисперсии. Выборочной дисперсией ${\displaystyle d_{B}}$ называется среднее арифметическое квадратов отклонений наблюдаемых значений от выборочного среднего: ${\displaystyle d_{B}={\frac {\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}_{B}\right)^{2}}{n}}}$.

Выборочным средним квадратичным отклонением называется арифметический квадратный корень из выборочной дисперсии: ${\displaystyle \sigma _{B}={\sqrt {d_{B}}}}$.

Рассматривая выборочные значения ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ как реализации случайных величин ${\displaystyle X_{1},X_{2},...,X_{n}}$, получивших конкретные значения в результате опытов, представим оценку ${\displaystyle \theta }$ как функцию этих случайных величин: ${\displaystyle \theta =\varphi \left(X_{1},X_{2},...,X_{n}\right)}$. Значит, что оценка тоже является случайной величиной. Если теперь определить математическое ожидание случайной величины ${\displaystyle \theta }$, то оно может совпасть или не совпасть с оцениваемым параметром^[3]:

Несмещённой называется статистическая оценка, математическое ожидание которой равно оцениваемому параметру: ${\displaystyle M(\theta )=\theta }$. В противном случае оценка называется смещённой.

Выборочная средняя ${\displaystyle {\bar {x}}_{B}}$ является несмещённой оценкой, а выборочная дисперсия ${\displaystyle d_{B}}$ — смещённой.

Чтобы «исправить» выборочную дисперсию, её нужно умножить на дробь ${\displaystyle {\frac {n}{n-1}}}$ . В результате получают «исправленную» выборочную дисперсию: ${\displaystyle S^{2}=\left[{\frac {n}{n-1}}\right]D_{B}}$, а для конкретной выборки ${\displaystyle s^{2}=\left[{\frac {n}{n-1}}\right]d_{B}}$. «Исправленным» выборочным средним квадратичным отклонением называется арифметический квадратный корень из «исправленной» выборочной дисперсии^[4].

Среднее квадратичное отклонение выборочной средней равно ${\displaystyle \sigma ({\bar {X}}_{B})={\sqrt {\frac {D_{x}}{n}}}={\frac {\sigma _{x}}{\sqrt {n}}}}$.

Для произвольной нормально распределённой случайной величины существует «Правило трёх сигм»^[5]:

Случайная величина ${\displaystyle \xi }$, распределённая по нормальному закону ${\displaystyle N(a,\sigma ^{2})}$, с вероятностью ${\displaystyle 0,9973}$ попадает в интервал ${\displaystyle (a-3\sigma ,a+3\sigma )}$, где ${\displaystyle a=M\xi }$ — математическое ожидание случайной величины.

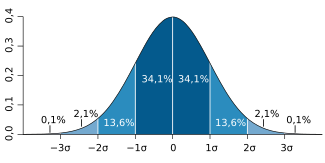
График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению

• В описательной статистике статистические показатели принято разбивать на несколько групп. Среднеквадратическое отклонение относится к показателям разброса, которые описывают степень разброса данных относительно своего центра (наряду с дисперсией выборки, размахом выборки и др.). Эти показатели говорят, насколько кучно основная масса данных группируется около центра^[5]. Среднеквадратическое отклонение используют вместо дисперсии случайной величины в случаях, когда необходимо, чтобы показатель разброса случайной величины выражался в тех же единицах, что и значение этой случайной величины^[6].
• В корреляционном анализе простейшим приёмом является нахождение коэффициента корреляции по принципу вариационных рядов. В этом случае расчёт коэффициента корреляции при оценке степени взаимосвязи двух рядов динамики ${\displaystyle X_{t}}$ и ${\displaystyle Y_{t}}$ определяется по следующей формуле:

${\displaystyle \mathbf {r} _{XY}={\frac {\mathbf {cov} _{XY}}{\mathbf {\sigma } _{X}{\sigma }_{Y}}}}$, где ${\displaystyle \mathbf {cov} _{XY}}$ — ковариация случайных величин ${\displaystyle X}$ и ${\displaystyle Y}$, а ${\displaystyle \sigma _{X},\sigma _{Y}}$ — их среднеквадратичные отклонения^[3].

• В техническом анализе рынков среднеквадратическое отклонение используется для построения линий Боллинджера, создающих рамку, в пределах которой цены считаются нормальными. Линии Боллинджера строятся в виде верхней и нижней границы вокруг скользящей средней, но ширина полосы не статична, а пропорциональна среднеквадратическому отклонению от скользящей средней за анализируемый период времени^[7].