Нечёткая логика

Нечёткая логика (англ. fuzzy logic) — разновидность многозначной логики, в которой истинностное значение переменных может принимать любое вещественное число между 0 и 1. Нечёткая логика используется для описания частичной истинности, когда значение может варьироваться между полностью истинным и полностью ложным. В отличие от этого, в булевой логике истинностные значения могут быть только 0 или 1.

Термин «нечёткая логика» был введён в 1965 году математиком Лотфи Заде в его публикации о нечётких множествах. Тем не менее, предпосылки для нечёткой логики рассматривались ещё в 1920-х годах в рамках бесконечномерной логики, в частности Яном Лукасевичем и Альфредом Тарским.

Нечёткая логика основывается на наблюдении, что люди принимают решения на основании неточной и недоопределённой информации. Нечёткие модели или нечёткие множества служат математическим инструментом для формализации неопределённости и неточных данных (отсюда и название). Такие модели позволяют распознавать, представлять, интерпретировать и использовать данные, обладающие размытыми характеристиками и неопределённостью.

Нечёткая логика нашла применение в различных областях — от теории управления до искусственного интеллекта.

Обзор

Классическая логика допускает только абсолютно истинные или ложные выводы. Однако существуют высказывания с переменным откликом, например при попытке определить цвет по мнению людей в группе. В таких случаях истинность выводится на основании неполных или приблизительных знаний, и ответы отображаются на некотором спектре.

Как степени истинности, так и вероятности принимают значения от 0 до 1, что на первый взгляд делает их схожими. Нечёткая логика использует степень истинности как математическую модель для описания неопределённости, в то время как вероятность — это модель незнания.

Использование истинностных значений

Базовый пример применения нечёткой логики — характеристика различных поддиапазонов непрерывной переменной. Например, для управления температурой (например, в антиблокировочной системе) могут быть определены отдельные функции принадлежности, соответствующие отдельным диапазонам температур. Каждая из таких функций сопоставляет температуре значение истинности от 0 до 1. Эти значения затем используются для вычисления и принятия управленческих решений. Теория нечётких множеств является одним из способов описания неопределённости.

Лингвистические переменные

В практических приложениях нечёткой логики для упрощения формулировок правил часто используются нечисловые значения.

Лингвистическая переменная, такой как «возраст», может принимать значения «молодой» или «старый». Поскольку в естественном языке не всегда достаточно терминов для отображения всего диапазона, часто применяются модификаторы — например, «довольно» или «несколько», позволяющие уточнить значение: «довольно старый», «немного молодой» и т.д.

Нечёткие системы

Система Мамдани

Наиболее известной является основанная на правилах система Мамдани (англ. Ebrahim Mamdani). Она использует следующий алгоритм:

1. Фаззифицировать все входные значения через функции принадлежности нечётким множествам.
2. Выполнить все применимые правила из базы знаний для вычисления выходных функций.
3. Дефаззифицировать выходные функции для получения «чёткого» результата.

Фаззификация

Фаззификация — процесс преобразования числового входа системы в нечёткие множества с определённой степенью принадлежности. Эта степень может быть любой в интервале [0,1]: 0 — не принадлежит множеству, 1 — принадлежит полностью. Промежуточные значения отражают уровень неопределённости членства. Обычно такие множества описываются словами, и после назначении входного значения соответствующим множествам над ними можно производить логические операции в лингвистически обоснованной форме.

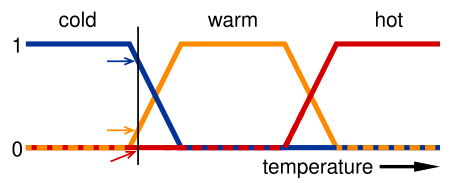
Например, на изображении ниже выражения «холодно», «тепло» и «жарко» представлены функциями, отображающими температурную шкалу. Точка на этой шкале может соответствовать трём значениям истинности — по одной для каждой функции. Например, синий цвет (0,8) — довольно холодно, оранжевый (0,2) — немного тепло, красный — 0 (не жарко). Соответственно, температура имеет степень принадлежности 0,2 к множеству «тепло» и 0,8 к «холодно».

Температурная шкала в нечёткой логике

Часто нечёткие множества определяются треугольными или трапециевидными функциями, т.е. с участком возрастания, пиком (где значение равно 1, с возможной ненулевой длиной) и убыванием. Также используются сигмоидальные функции. Одним из примеров служит стандартная логистическая функция:

$S(x)={\frac {1}{1+e^{-x}}}$

которая обладает симметрией:

$S(x)+S(-x)=1.$

Из этого следует:

$(S(x)+S(-x))\cdot (S(y)+S(-y))\cdot (S(z)+S(-z))=1$

Операторы нечёткой логики

Нечёткая логика работает с функциями принадлежности аналогично булевой логике, для чего вводятся аналоги булевых операций AND, OR, NOT — как правило, это так называемые операторы Заде:

Булева логика	Нечёткая логика
AND(x, y)	MIN(x, y)
OR(x, y)	MAX(x, y)
NOT(x)	1 – x

Для значений 1 (ИСТИНА) и 0 (ЛОЖЬ) результат совпадает с булевой логикой.

Существуют и другие операторы — т. н. «хеджес», выражающие нюансы языка («очень», «слегка», и др.), определяемые формулами.

Однако не любая таблица истинности определяет функцию нечёткой логики. В работе (Зайцев и др.) сформулирован критерий для распознавания, определяет ли заданная таблица выбора функцию нечёткой логики, и предложен алгоритм синтеза по концепции конституент минимумов и максимумов.

Альтернативный набор операторов основан на умножении:

x AND y = x * y
NOT x = 1 - x

x OR y = 1 - (1 - x) * (1 - y) = x + y - x*y

Имея две из операций AND/OR/NOT, третья выводится однозначно. Обобщением AND является t-норма.

IF-THEN правила

См. также: Нечёткое правило

Правила IF-THEN сопоставляют входные или вычисленные значения истинности требуемым выходным значениям, например:

IF температура ОЧЕНЬ ХОЛОДНАЯ ТО скорость_вентилятора = остановлен
IF температура ХОЛОДНАЯ ТО скорость_вентилятора = медленно
IF температура ТЁПЛАЯ ТО скорость_вентилятора = умеренно
IF температура ЖАРКАЯ ТО скорость_вентилятора = быстро

Если выходная переменная встречается в нескольких THEN, то значения комбинируются с помощью OR.

Дефаззификация

См. также: Дефаззификация

Требуется получить чёткое числовое значение на основании нечётких истинностных оценок.

Это делается путём сопоставления областей функций принадлежности соответствующим уровням истинности, поиском центра тяжести выделенной области и определением выходного значения по положению центра масс.

Однозначного алгоритма нет, хотя на практике часто применяют:

1. Для каждого уровня обрезать функцию принадлежности этим значением.
2. Объединить полученные кривые по OR.
3. Найти центр тяжести под кривой.
4. Абсцисса центра — конечный результат.

Система Такаги—Сугено—Канга (TSK)

Система TSK схожа с Мамдани, но включает дефаззификацию прямо на этапе применения правила. В качестве результата применяются полиномиальные функции (обычно линейные или постоянные). Например:

IF температура ОЧЕНЬ ХОЛОДНАЯ = 2

Здесь результат равен константе, аналогично, для обобщённого правила с двумя и более условиями результатом будет средневзвешенное всех выходов:

${\frac {\sum _{i}(h_{i}\cdot Y_{i})}{\sum _{i}h_{i}}}$

Аналогично для случая с линейной функцией:

IF температура ОЧЕНЬ ХОЛОДНАЯ И влажность ВЫСОКАЯ = 2 * температура + 1 * влажность

Здесь для вычисления берётся результат функции с параметрами как степени принадлежности. Для всех правил база знаний агрегируется средневзвешенным результатом.

Главное преимущество TSK — вычислительная эффективность, что делает её удобной для реализации в составе других методов (например, ПИД-регуляторов и адаптивных нейронных систем). Система Мамдани интуитивнее для пользователя, поэтому TSK обычно применяют в составе комплексных методов, таких как адаптивные нейронечёткие системы.

Согласование входов и нечётких правил

Поскольку выход нечёткой системы представляет консенсус по всем входам и правилам, такие системы устойчивы к отсутствию или недостоверности входных данных. Каждому правилу можно назначать вес, отражающий его приоритет, достоверность или согласованность. Вес может быть статичен или меняться динамически, что позволяет точно регулировать влияние отдельных правил на итоговые значения.

Применения

Нечёткая логика применяется в системах управления, позволяя экспертам формулировать нестрогие правила типа «если поезд близко к станции и движется быстро, увеличить тормозное усилие». Эти правила затем уточняются численно внутри системы.

Многие успешные ранние применения нечёткой логики были реализованы в Японии, в частности для метропоезда Сэндай — что позволило повысить комфорт, экономичность и точность движения. Также нечёткая логика применялась для распознавания рукописного ввода (устройства Sony), в авиационных помощниках, ЭВМ, управлении автотранспортом, бытовой технике (стиральные машины, пылесосы с автоматической регулировкой мощности), а также в системах раннего обнаружения землетрясений Сендайского бюро метеорологии Японии.

Искусственный интеллект

См. также: Нейронечёткая система

Нейронные сети и нечёткая логика близки по сути: нейросеть принимает множество входов, назначает им веса, несколько раз агрегирует промежуточные значения и формирует выход — без явно бинарных ветвлений, характерных для классической математики и программирования. В 1980-х годах велись споры о превосходстве подходов деревьев решений и нейросетей — первые отражают бинарную логику аппаратных устройств, но не дают желаемого качества, тогда как нейросети формируют сложные модели на практике. Сегодня такие системы реализуются и в аналоговой схемотехнике, что даёт выигрыш по энергоэффективности при допустимых погрешностях.

Медицинские решения

Нечёткая логика важна для медицинских экспертных систем, т.к. многие медицинские данные субъективны и нечетки.

Методы нечёткой логики применяются для анализа медицинских изображений, сигналов, сегментации данных и извлечения признаков. Главной проблемой является получение достаточного объёма доверительных «нечётких» данных для образования надёжных оценок.

Компьютерный диагноз по изображениям

Одна из распространённых сфер применения нечёткой логики — автоматизированный (поддерживаемый компьютером) диагноз по медицинским изображениям.

Нечёткие базы данных

Появление формальных средств задания нечётких отношений дало возможность создавать нечёткие реляционные базы данных. Первая подобная модель (FRDB) была предложена Марией Земанковой (1983). Позднее появились альтернативные модели: Баклза—Петри, Прада—Тестемаля, Умано—Фуками, GEFRED.

Для работы с такими данными разработаны языки запросов, поддерживающие нечёткие условия (например, SQLf, FSQL).

Логический анализ

В математической логике выделяют ряд формальных систем нечёткой логики, из которых большинство относятся к классу t-норм-неклассических логик.

Высказывательные нечёткие логики

Наиболее исследованные системы:

• Логика t-норм (MTL) — аксиоматизирована на основе левосторонней t-нормы (конъюнкция) и резидуального условия для импликации, модели — MTL-алгебры (полулинейные интегральные коммутативные решётки).
• Базовая нечёткая логика (BL) — расширение MTL, где конъюнкция определяется непрерывной t-нормой.
• Лукасевичева нечёткая логика — расширение BL с t-нормой Лукасевича (основа — двойное отрицание), модели — MV-алгебры.
• Нечёткая логика Гёделя — конъюнкция через t-норму Гёделя (минимум), есть аксиома идемпотентности, модели — G-алгебры.
• Нечёткая логика произведения — с операцией умножения как t-нормой, с аксиомой сокращаемости произведения, модели — алгебры произведений.
• Оценочная логика (EVŁ, логика Павелки) — обобщает синтаксис и семантику, позволяет каждой формуле иметь числовую оценку, обобщая теорему Гёделя о полноте.

Предикатные нечёткие логики

По аналогии с переходом от высказывательной к предикатной классической логике, в нечёткой логике возможно введение универсальных и существующих кванторов. Для интерпретации используют инфимум (для ∀) и супремум (для ∃) всех оценок.

Вопросы разрешимости

Понятия разрешимых и перечислимых множеств важны для классической математики и логики. Первые попытки их обобщения для нечётких множеств (фаззи-Тьюринг-машина, фаззи-программа) были предприняты E. S. Santos (1970). Позже Л. Бьячино и Дж. Герла показали, что попробованные определения некорректны для теории языков. Они предложили строгие определения: нечёткое множество s: S → [0,1] называется разрешимо перечислимым, если существует рекурсивная функция h: S×N → Q∩[0,1], возрастающая по n и сходящаяся к s(x). s разрешимо, если и s, и его дополнение разрешимо перечислимы. Любая строго аксиоматизированная теория нечёткой логики перечислима, и для некоторых случаев (полных теорий) разрешима.

Открытым остаётся вопрос о формулировке аналога тезиса Черча для нечёткой математики.

Сравнение с другими логиками

Вероятность

Нечёткая логика и вероятностная теория описывают разные аспекты неопределённости. В то время как обе могут выражать субъективную степень уверенности, нечёткая логика — это степень принадлежности к нестрого определённому множеству, а вероятность — частота или вероятность события. Концепция нечётких множеств развивалась в середине XX века в Беркли как ответ на отсутствие моделей одновременно для неопределённости и нечеткости.

Барт Коско (англ. Bart Kosko) утверждает, что вероятностная теория есть частный случай нечёткой логики. Лотфи Заде подчеркивал различие этих подходов, развил понятие нечеткой вероятности и предложил теорию возможностей.

В целом нечёткая логика является лишь одним из инструментов моделирования неопределённости, вызывающей трудности для классической логики и вероятности (например, теории Демпстера — Шефера).

Экоритмы

Теоретик вычислений Лесли Валиант (англ. Leslie Valiant) предложил термин экоритмы как обозначение подходов, подобных нечёткой логике, основанных на обучении на сложной среде. Такие методы позволяют учитывать непрерывное множество состояний среды без необходимости полного перечисления.

Логика Гёделя G_∞

См. также: G_∞-логика

Система, в которой значения истинности — числа на интервале [0,1], а AND/OR реализуются как MIN/MAX, — это логика Гёделя G_∞. Особенность здесь — иная дефиниция отрицания и импликации, делающая систему пригодной, например, для моделирования интуиционистской логики.

Компенсаторная нечёткая логика

Компенсаторная нечёткая логика — направление, в котором операции конъюнкции и дизъюнкции модифицированы так, что изменение одного компонента компенсируется изменением другого, возможно до определённого предела (порогового значения). Эта логика приближена к семантике естественного языка.

Стандартизация языков разметки

IEEE 1855 — стандарт на язык Fuzzy Markup Language (FML), разработанный IEEE для описания нечётких систем в открытом и аппаратно-независимом виде на базе XML. До появления FML обмен алгоритмами вёлся через обмен поддержкой Fuzzy Control Language (FCL) по стандарту IEC 61131.

См. также

• Случайная нечёткая переменная
• Операторы OWA типа 1
• Нечёткое понятие
• Построение t-норм
• Взвешенное усреднение по порядку

Примечания

Литература

• Arabacioglu, B. C. (2010). “Using fuzzy inference system for architectural space analysis”. Applied Soft Computing. 10 (3): 926—937. DOI:10.1016/j.asoc.2009.10.011.
• Biacino, Loredana; Gerla, Giangiacomo (1 октября 2002). “Fuzzy logic, continuity and effectiveness”. Archive for Mathematical Logic. 41 (7): 643—667. CiteSeerX 10.1.1.2.8029. DOI:10.1007/s001530100128. S2CID 12513452.
• The fuzzy systems handbook: a practitioner's guide to building, using, maintaining fuzzy systems. — Boston : AP Professional, 1994. — ISBN 978-0-12-194270-0.
• Gerla, Giangiacomo (март 2006). “Effectiveness and multivalued logics”. Journal of Symbolic Logic. 71 (1): 137—162. DOI:10.2178/jsl/1140641166. S2CID 12322009.
• Metamathematics of fuzzy logic. — Dordrecht : Kluwer, 1998. — ISBN 978-0-7923-5238-9.
• Hájek, Petr (август 1995). “Fuzzy logic and arithmetical hierarchy”. Fuzzy Sets and Systems. 73 (3): 359—363. DOI:10.1016/0165-0114(94)00299-M.
• Reasoning about uncertainty. — Cambridge, Massachusetts : MIT Press, 2003. — ISBN 978-0-262-08320-1.
• Fuzzy cluster analysis: methods for classification, data analysis and image recognition. — New York : John Wiley, 1999. — ISBN 978-0-471-98864-9.
• Introduction to Applied Fuzzy Electronics. — Englewood Cliffs, NJ : Prentice Hall, 1997. — ISBN 978-0-13-206400-2.
• Fuzzy sets, uncertainty, and information. — Englewood Cliffs, NJ : Prentice Hall, 1988. — ISBN 978-0-13-345984-5.
• Fuzzy set theory: foundations and applications. — Englewood Cliffs, NJ : Prentice Hall, 1997. — ISBN 978-0-13-341058-7.
• Fuzzy sets and fuzzy logic: theory and applications. — Upper Saddle River, NJ : Prentice Hall PTR, 1995. — ISBN 978-0-13-101171-7.
• Fuzzy thinking: the new science of fuzzy logic. — New York : Hyperion, 1993. — ISBN 978-0-7868-8021-8.
• Kosko, Bart; Isaka, Satoru (июль 1993). “Fuzzy Logic”. Scientific American. 269 (1): 76—81. Bibcode:1993SciAm.269a..76K. DOI:10.1038/scientificamerican0793-76.
• Lohani, A. K.; Goel, N. K.; Bhatia, K. K. S. (2006). “Takagi–Sugeno fuzzy inference system for modeling stage–discharge relationship”. Journal of Hydrology. 331 (1): 146—160. Bibcode:2006JHyd..331..146L. DOI:10.1016/j.jhydrol.2006.05.007.
• Lohani, A. K.; Goel, N. K.; Bhatia, K. K. S. (2007). “Deriving stage–discharge–sediment concentration relationships using fuzzy logic”. Hydrological Sciences Journal. 52 (4): 793—807. Bibcode:2007HydSJ..52..793L. DOI:10.1623/hysj.52.4.793. S2CID 117782707.
• Lohani, A. K.; Goel, N. K.; Bhatia, K. K. S. (2012). “Hydrological time series modeling: A comparison between adaptive neuro-fuzzy, neural network and autoregressive techniques”. Journal of Hydrology. 442–443 (6): 23—35. Bibcode:2012JHyd..442...23L. DOI:10.1016/j.jhydrol.2012.03.031.
• Masmoudi, Malek; Haït, Alain (ноябрь 2012). “Fuzzy uncertainty modelling for project planning; application to helicopter maintenance” (PDF). International Journal of Production Research. 50 (24). Архивировано из оригинала (PDF) 2017-09-22.
• Merigó, José M.; Gil-Lafuente, Anna M.; Yager, Ronald R. (февраль 2015). “An overview of fuzzy research with bibliometric indicators”. Applied Soft Computing. 27: 420—433. DOI:10.1016/j.asoc.2014.10.035.
• Mironov, A. M. (август 2005). “Fuzzy Modal Logics”. Journal of Mathematical Sciences. 128 (6): 3461—3483. DOI:10.1007/s10958-005-0281-1. S2CID 120674564.
• Montagna, Franco (2001). “Three complexity problems in quantified fuzzy logic”. Studia Logica. 68 (1): 143—152. DOI:10.1023/A:1011958407631. S2CID 20035297.
• Algebraic foundations of many-valued reasoning. — Dordrecht : Kluwer Academic, 1999. — ISBN 978-0-7923-6009-4.
• Fuzzy Sets and Their Applications. — Bristol : Adam Hilger, 1989. — ISBN 978-0-85274-583-0.
• Novák, Vilém (2005). “On fuzzy type theory”. Fuzzy Sets and Systems. 149 (2): 235—273. DOI:10.1016/j.fss.2004.03.027.
• Mathematical principles of fuzzy logic. — Dordrecht : Kluwer Academic, 1999. — ISBN 978-0-7923-8595-0.
• Onses, Richard. Second Order Experton: A new Tool for Changing Paradigms in Country Risk Calculation. — Universidad, Secretariado de Publicaciones, 1996. — ISBN 978-84-7719-558-0.
• Onses, Richard. Détermination de l'incertitude inhérente aux investissements en Amérique Latine sur la base de la théorie des sous ensembles flous. — Barcelona : Universitat de Barcelona, 1994. — ISBN 978-84-475-0881-5.
• Fuzzy control. — Boston : Addison-Wesley, 1998. — ISBN 978-0-201-18074-9.
• Fuzzy systems engineering: Toward Human-centric Computing. — Hoboken : Wiley-Interscience, 2007. — ISBN 978-0-471-78857-7.
• Pao-Ming, Pu; Ying-Ming, Liu (август 1980). “Fuzzy topology. I. Neighborhood structure of a fuzzy point and Moore-Smith convergence”. Journal of Mathematical Analysis and Applications. 76 (2): 571—599. DOI:10.1016/0022-247X(80)90048-7.
• Sahoo, Bhabagrahi; Lohani, A. K.; Sahu, Rohit K. (2006). “Fuzzy multiobjective and linear programming based management models for optimal land-water-crop system planning”. Water Resources Management. 20 (6): 931—948. Bibcode:2006WatRM..20..931S. DOI:10.1007/s11269-005-9015-x. S2CID 154264034.
• Santos, Eugene S. (1970). “Fuzzy Algorithms”. Information and Control. 17 (4): 326—339. DOI:10.1016/S0019-9958(70)80032-8.
• Scarpellini, Bruno (июнь 1962). “Die nichtaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz”. Journal of Symbolic Logic. 27 (2): 159—170. DOI:10.2307/2964111. HDL:20.500.11850/423097. JSTOR 2964111. S2CID 26330059.
• The Fuzzification of Systems. The Genesis of Fuzzy Set Theory and Its Initial Applications -- Developments up to the 1970s. — Springer-Verlag, 2007. — ISBN 978-3-540-71795-9.
• The Nonlinear Workbook: Chaos, Fractals, Cellular Automata, Neural Networks, Genetic Algorithms, Gene Expression Programming, Support Vector Machine, Wavelets, Hidden Markov Models, Fuzzy Logic with C++, Java and SymbolicC++ Programs. — 4. — World Scientific, 2008. — ISBN 978-981-281-852-2.
• Neural Cell Behavior and Fuzzy Logic. — Springer, 2008. — ISBN 978-0-387-09542-4.
• Wiedermann, J. (2004). “Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines”. Theoretical Computer Science. 317 (1—3): 61—69. DOI:10.1016/j.tcs.2003.12.004.
• Essentials of fuzzy modeling and control. — New York : Wiley, 1994. — ISBN 978-0-471-01761-5.
• Fuzzy Logic Applied to Daily Life. — Seattle, WA : No No No No Press, 2008. — ISBN 978-0-252-16341-8.
• Fuzzy logic and NeuroFuzzy applications explained. — Upper Saddle River, NJ : Prentice Hall PTR, 1995. — ISBN 978-0-13-368465-0.
• Wilkinson, R. H. (1963). “A method of generating functions of several variables using analog diode logic”. IEEE Transactions on Electronic Computers. 12 (2): 112—129. DOI:10.1109/PGEC.1963.263419.
• Zadeh, L. A. (февраль 1968). “Fuzzy algorithms”. Information and Control. 12 (2): 94—102. DOI:10.1016/S0019-9958(68)90211-8.
• Zaitsev, D. A.; Sarbei, V. G.; Sleptsov, A. I. (1998). “Synthesis of continuous-valued logic functions defined in tabular form”. Cybernetics and Systems Analysis. 34 (2): 190—195. DOI:10.1007/BF02742068. S2CID 120220846.
• Fuzzy set theory and its applications. — Boston : Kluwer Academic Publishers, 2001. — ISBN 978-0-7923-7435-0.

Ссылки

• IEC 1131-7 CD1 — спецификация стандарта IEC 1131-7
• Fuzzy Logic — статья в Scholarpedia
• Modeling With Words — статья Scholarpedia
• Fuzzy logic — статья в Stanford Encyclopedia of Philosophy
• Fuzzy Math — введение в нечёткую логику
• Fuzziness and exactness — обсуждение неточности в жизни и науке
• Fuzzylite — кроссплатформенная библиотека нечёткого управления (C++/QT4)
• More Flexible Machine Learning — пример применения MIT
• Semantic Similarity — реализованные детали семантики нечёткости (MIT)