Квантовая запутанность
Ква́нтовая запу́танность[1][2] — квантовомеханическое явление, при котором квантовые состояния двух или большего числа объектов оказываются взаимозависимыми. Например, можно получить пару фотонов, находящихся в запутанном состоянии, и тогда если при измерении спина первой частицы её спиральность оказывается положительной, то спиральность второй всегда оказывается отрицательной, и наоборот.
Такая взаимозависимость сохраняется, даже если эти объекты разнесены в пространстве за пределы любых известных взаимодействий. Измерение параметра одной частицы сопровождается мгновенным (быстрее скорости света[3]) прекращением запутанного состояния другой, что может находиться в логическом противоречии с принципом локальности, но при этом информация не передаётся и теория относительности не нарушается.
История изучения
На Пятом Сольвеевском конгрессе 1927 года одним из центров дискуссии стал спор Бора и Эйнштейна о принципах Копенгагенской интерпретации квантовой механики[4], которая, впрочем, ещё не имела этого названия, закрепившегося только в 1950-е годы[5]. Эйнштейн настаивал на сохранении в квантовой физике принципов детерминизма классической физики и на трактовке результатов измерения с точки зрения «несвязанного наблюдателя» (англ. «detached observer»). С другой стороны, Бор настаивал на принципиально недетерминированном (стохастическом) характере квантовых явлений и на неустранимости эффекта влияния измерения на само состояние. Как квинтэссенция этих споров часто приводится диалог Эйнштейна с Бором: «— Бог не играет в кости. — Альберт, не указывай Богу, что ему делать.», а также саркастический вопрос Эйнштейна: «Вы действительно считаете, что Луна существует, только когда вы на неё смотрите?»[6]
В продолжение начавшихся споров в 1935 году Эйнштейн, Подольский и Розен сформулировали ЭПР-парадокс, который должен был показать неполноту предлагаемой модели квантовой механики. Их статья «Можно ли считать квантово-механическое описание физической реальности полным?» была опубликована в № 47 журнала «Physical Review»[7].
В ЭПР-парадоксе мысленно нарушался принцип неопределённости Гейзенберга: при наличии двух частиц, имеющих общее происхождение, можно измерить состояние одной частицы и по нему предсказать состояние другой, над которой измерение ещё не производилось. Анализируя в том же году подобные теоретически взаимозависимые системы, Шрёдингер назвал их «спутанными» (англ. entangled)[8]. Позднее англ. entangled и англ. entanglement стали общепринятыми терминами в англоязычных публикациях[9]. Сам Шрёдингер считал частицы запутанными, только пока они физически взаимодействовали друг с другом. При удалении за пределы возможных взаимодействий запутанность исчезала[9]. То есть значение термина у Шрёдингера отличается от того, которое подразумевается в настоящее время.
Эйнштейн не рассматривал ЭПР-парадокс как описание какого-либо действительного физического феномена. Это была именно мысленная конструкция, созданная для демонстрации противоречий принципа неопределённости. В 1947 году в письме Максу Борну он назвал подобную связь между запутанными частицами «призрачным дальнодействием» (нем. spukhafte Fernwirkung, англ. spooky action at a distance в переводе Борна)[10]:
Поэтому я не могу в это поверить, так как (эта) теория непримирима с принципом того, что физика должна отражать реальность во времени и пространстве, без (неких) призрачных дальнодействий.
Оригинальный текст (нем.)[показатьскрыть]Ich kann aber deshalb nicht ernsthaft daran glauben, weil die Theorie mit dem Grundsatz unvereinbar ist, dass die Physik eine Wirklichkeit in Zeit und Raum darstellen soll, ohne spukhafte Fernwirkungen.— «Entangled systems: new directions in quantum physics»[11]
Уже в следующем номере «Physical Review» Бор опубликовал свой ответ в статье с таким же заголовком, как и у авторов парадокса[12]. Сторонники Бора посчитали его ответ удовлетворительным, а сам ЭПР-парадокс — вызванным неправильным пониманием сути «наблюдателя» в квантовой физике Эйнштейном и его сторонниками[9]. В целом большинство физиков просто устранилось от философских сложностей Копенгагенской интерпретации. Уравнение Шрёдингера работало, предсказания совпадали с результатами, и в рамках позитивизма этого было достаточно. Гриббин пишет по этому поводу[13]: «чтобы добраться из точки А в точку Б, водителю необязательно знать, что происходит под капотом его машины». Эпиграфом же к своей книге Гриббин поставил слова Фейнмана:
Думаю, я могу ответственно заявить, что никто не понимает квантовую механику. Если есть возможность, прекратите спрашивать себя «Да как же это возможно?» — так как вас занесёт в тупик, из которого ещё никто не выбирался.
Такое состояние дел оказалось не слишком удачным для развития физической теории и практики. «Запутанность» и «призрачные дальнодействия» игнорировались почти 30 лет[9], пока ими не заинтересовался ирландский физик Джон Белл. Вдохновлённый идеями Бома[14] (теория де Бройля — Бома), Белл продолжил анализ ЭПР-парадокса и в 1964 сформулировал свои неравенства[15][16]. Весьма упрощая математические и физические составляющие, можно сказать, что из работы Белла следовали две однозначно распознаваемые ситуации при статистических измерениях состояний запутанных частиц. Если состояния двух запутанных частиц определённы в момент разделения, то должно выполняться одно неравенство Белла. Если состояния двух запутанных частиц неопределённы до измерения состояния одной из них, то должно выполняться другое неравенство.
Неравенства Белла предоставили теоретическую базу для возможных физических экспериментов, однако по состоянию на 1964 год техническая база не позволяла ещё их поставить. Первые успешные эксперименты по проверке неравенств Белла были осуществлены Клаузером и Фридманом в 1972 году[17]. Из результатов следовала неопределённость состояния пары запутанных частиц до проведения измерения над одной из них. И всё же вплоть до 1980-х годов большинство физиков рассматривали квантовую сцеплённость «не как новый неклассический ресурс, который можно использовать, а скорее как конфуз, ждущий окончательного разъяснения»[9].
Однако за экспериментами группы Клаузера последовали эксперименты Аспе в 1981 году[17]. В классическом эксперименте Аспе (см. схему) два потока фотонов с нулевым суммарным спином, вылетавшие из источника S, направлялись на призмы Николя a и b. В них за счёт двойного лучепреломления происходило разделение поляризаций каждого из фотонов на элементарные, после чего пучки направлялись на детекторы D+ и D-. Сигналы от детекторов через фотоумножители поступали в регистрирующее устройство R, где вычислялось неравенство Белла.
Результаты, полученные как в опытах Фридмана — Клаузера, так и в опытах Аспе, чётко говорили в пользу отсутствия эйнштейновского локального реализма: «призрачное дальнодействие» из мысленного эксперимента окончательно стало физической реальностью. Последний удар по локальности был нанесён в 1989 году многосвязными состояниями Гринбергера — Хорна — Цайлингера[18], заложившими базис квантовой телепортации. В 2010 году Джон Клаузер, Ален Аспе и Антон Цайлингер стали лауреатами премии Вольфа по физике «за фундаментальный концептуальный и экспериментальный вклад в основы квантовой физики, в частности за серию возрастающих по сложности проверок неравенств Белла (или расширенных версий этих неравенств) с использованием запутанных квантовых состояний»[19].
Лауреаты премии Вольфа по физике 2010 года
Современные версии описанного выше эксперимента создают сегменты Sa и Sb такой длины, чтобы регистрация фотонов происходила в заведомо не связанных известными взаимодействиями областях пространства-времени. В 2007 году исследователям из Мичиганского университета удалось разнести запутанные фотоны на рекордное в тот момент расстояние в 1 м[20][21].
В 2008 году группе швейцарских исследователей из Университета Женевы удалось разнести два потока запутанных фотонов на расстояние 18 километров. Помимо прочего, это позволило произвести временны́е измерения с недостижимой ранее точностью. В результате было установлено, что если некое скрытое взаимодействие и происходит, то скорость его распространения должна как минимум в 100 000 раз превышать скорость света в вакууме. При меньшей скорости временные задержки были бы замечены[22][23].
Летом того же года другой группе исследователей из австрийского Института квантовой оптики и квантовой информации, включая Цайлингера, удалось поставить ещё более масштабный эксперимент, разнеся потоки запутанных фотонов на 144 километра, между лабораториями на островах Пальма и Тенерифе. Обработка и анализ столь масштабного эксперимента продолжаются, последняя версия отчёта была опубликована в 2010 году[24][25]. В данном эксперименте удалось исключить возможное влияние недостаточного расстояния между объектами в момент измерения и недостаточной свободы выбора настроек измерения. В результате были ещё раз подтверждены квантовая запутанность и, соответственно, нелокальная природа реальности. Правда, осталось третье возможное влияние — недостаточно полной выборки. Эксперимент, в котором все три потенциальных влияния будут исключены одновременно, на сентябрь 2011 года является вопросом будущего.
В большинстве экспериментов с запутанными частицами используются фотоны. Это объясняется относительной простотой получения запутанных фотонов и их передачи в детекторы, а также бинарной природой измеряемого состояния (положительная или отрицательная спиральность). Однако явление квантовой запутанности существует и для других частиц и их состояний. В 2010 году международный коллектив учёных из Франции, Германии и Испании получил и исследовал[26][27] запутанные квантовые состояния электронов, то есть частиц с массой, в твёрдом сверхпроводнике из углеродных нанотрубок. В 2011 году исследователям из Института квантовой оптики общества Макса Планка удалось создать состояние квантовой запутанности между отдельным атомом рубидия и конденсатом Бозе — Эйнштейна, разнесёнными на расстояние 30 м[28][29].
В 2017 г. удалось экспериментально зафиксировать связанные состояния из трёх фотонов внутри облака атомов рубидия, возникающие под действием лазерных импульсов[30].
Название явления в русскоязычных источниках
При устойчивом английском термине quantum entanglement, достаточно последовательно использующимся в англоязычных публикациях, русскоязычные работы демонстрируют широкое разнообразие узуса. Из встречающихся в источниках по теме терминов можно назвать (в алфавитном порядке):
- Запутанные квантовые состояния[31]
- Квантовая запутанность
- Квантовая зацепленность[32]
- Квантовые корреляции[33][34] (термин неудачен из-за неоднозначности[35][36])
- Квантовая нелокальность[37]
- Квантовая перепутанность[38]
- Несепарабельность[39] (как уточнение к «квантовым корреляциям»)
- Квантовая сцепленность[1]
В популярной прессе употребляется также выражение «квантовая спутанность»[40].
Такое разнообразие можно объяснить несколькими причинами, в том числе объективным наличием двух обозначаемых объектов: а) само состояние (англ. quantum entanglement) и б) наблюдаемые эффекты в этом состоянии (англ. spooky action at a distance), которые во многих русскоязычных работах различаются по контексту, а не терминологически.
Математическая формулировка
Получение запутанных квантовых состояний
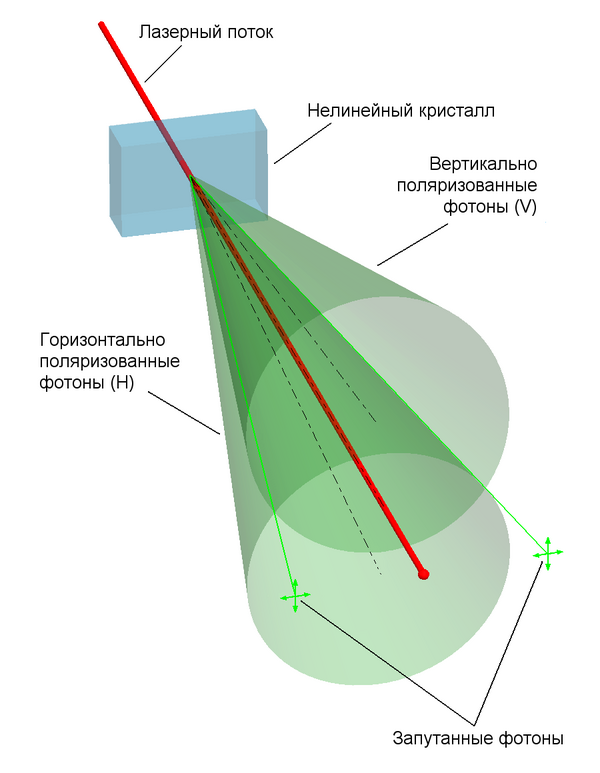
В простейшем случае источником S потоков запутанных фотонов служит определённый нелинейный материал, на который направляется лазерный поток определённой частоты и интенсивности (схема с одним эмиттером)[41]. В результате спонтанного параметрического рассеяния (СПР) на выходе получаются два конуса поляризации H и V, несущие пары фотонов в запутанном квантовом состоянии (бифотоны)[42].
| подробнее[43] |
|---|
| При СПР типа II под воздействием поляризованного лазерного излучения накачки в кристалле бета-бората бария спонтанно рождаются бифотоны, сумма частот которых равна частоте излучения накачки:
ω1 + ω2 = ω а поляризации ортогональны в базисе, определяемом ориентацией кристалла. Благодаря двойному лучепреломлению, при определённых условиях фотоны имеют одну частоту и излучаются вдоль двух конусов, не имеющих общей оси. При этом в одном конусе поляризация вертикальная, а во втором — горизонтальная (по отношению к ориентации кристалла и поляризации излучения накачки). При СПР для волновых векторов также верно
поэтому, если забирать один фотон бифотонной пары из одной линии пересечения конусов, то второй фотон можно всегда забрать из второй линии пересечения. В кристалле фотоны разных поляризаций распространяются с разной скоростью, поэтому в реальной экспериментальной установке каждый пучок дополнительно пропускается через такой же кристалл половинной толщины, повёрнутый на 90°. Кроме того, для нивелирования поляризационных эффектов, в одном из пучков вертикальная и горизонтальная поляризации меняются местами при помощи комбинации полуволновой и четвертьволновой пластинок. Создаваемые в результате СПР члены бифотонной пары можно обозначить индексами 1 и 2, при этом:
По аналогии с двухщелевым экспериментом два возможных варианта измерений поляризации (после поворота в одном из пучков поляризации одинаковы) можно описать суперпозицией произведений и , а возможные варианты измерения пространственных мод и . Так как состояние поляризации и пространственные моды независимы друг от друга, то общая волновая функция принимает вид:
Фотоны являются бозонами, поэтому волновая функция пары фотонов должна быть симметрична относительно перестановки индексов. В результате симметризации получаем:
Ориентацией компенсационных кристаллов фазовый множитель можно привести к 1 и мы получаем окончательный вид волновой функции бифотона:
Множитель, описывающий состояние поляризации, является одним из четырёх белловских максимально запутанных состояний:
|
Выбор конкретного материала зависит от задач эксперимента, используемой частоты и мощности[44][45]. В таблице ниже приводятся лишь некоторые часто используемые неорганические нелинейные кристаллы с регулярной доменной структурой[46] (РДС-кристаллы, англ. periodically poled):
| Вещество | Формула | Аббревиатура |
|---|---|---|
| бета-борат бария | β-BaB2O4 | BBO |
| триборат лития | LiB3O5 | LBO |
| титанил фосфат калия | KTiOPO4 | KTP |
| ниобат калия | KNbO3 | — |
Интересным и сравнительно молодым направлением стали нелинейные кристаллы на органической основе[47][48]. Предполагалось, что органические составляющие живых организмов должны обладать сильными нелинейными свойствами из-за позиций орбиталей в π-связях. Эти предположения подтвердились, и несколькими группами исследователей были получены высококачественные нелинейные кристаллы путём дегидратации насыщенных растворов аминокислот. Некоторые из этих кристаллов:
| Вещество | Формула | Аббревиатура |
|---|---|---|
| L-аргинин малеин дигидрат | C6H14N4O2 + C4H4O4 | LAMD |
| 2-L-метионин малеин дигидрат | C5H11NO2S + C4H4O4 | LMMM |
LMMM из таблицы получается кристаллизацией смеси в пропорции два к одной L-метионина (метаболическое средство) и малеиновой кислоты (пищевая промышленность), то есть из массово производимых веществ. При этом эффективность правильно выращенного кристалла составляет 90 % от более дорогого и труднодоступного неорганического KTP[48].
Идеи применения
Всего через год после эксперимента Аспэ, в 1982 году, американский физик Ник Херберт предложил журналу «Foundations of Physics» статью с идеей своего «сверхсветового коммуникатора на основе нового типа квантовых измерений» FLASH (First Laser-Amplified Superluminal Hookup). По позднейшему рассказу Ашера Переса[49], бывшего в тот момент одним из рецензентов журнала, ошибочность идеи была очевидной, но, к своему удивлению, он не нашёл конкретной физической теоремы, на которую мог бы кратко сослаться. Поэтому он настоял на публикации статьи, так как это «пробудит заметный интерес, а нахождение ошибки приведёт к заметному прогрессу в нашем понимании физики». Статья была напечатана[50], и в результате развернувшейся дискуссии Вуттерсом, Зуреком и Диксом была сформулирована и доказана теорема о запрете клонирования. Так излагается история у Переса в его статье, опубликованной 20 лет спустя после описываемых событий.
Теорема о запрете клонирования утверждает невозможность создания идеальной копии произвольного неизвестного квантового состояния. Весьма упрощая ситуацию, можно привести пример с клонированием живых существ. Можно создать идеальную генетическую копию овцы, но нельзя «клонировать» жизнь и судьбу прототипа.
Учёные обычно скептически относятся к проектам со словом «сверхсветовой» в названии. К этому добавился неортодоксальный научный путь самого Херберта. В 1970-х он вместе с приятелем из Xerox PARC сконструировал «метафазовую печатную машинку» для «коммуникации с бесплотными духами»[51] (результаты интенсивных экспериментов были признаны участниками непоказательными). А в 1985 Херберт написал книгу о метафизическом в физике[52]. В целом, события 1982 года достаточно сильно скомпрометировали идеи квантовой коммуникации в глазах потенциальных исследователей, и до конца XX века существенного прогресса в этом направлении не наблюдалось.
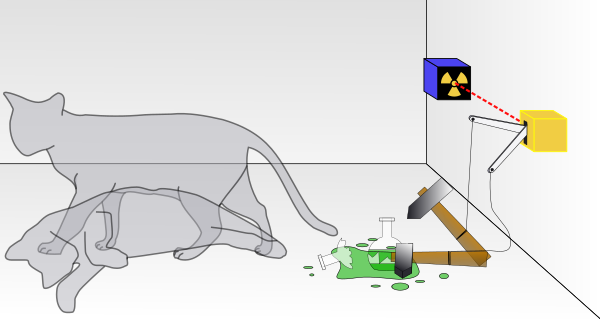
Теория квантовой механики запрещает передачу информации со сверхсветовой скоростью. Это объясняется принципиально вероятностным характером измерений и теоремой о запрете клонирования. Представим разнесённых в пространстве наблюдателей А и Б, у которых имеется по экземпляру квантово-запутанных ящиков с котами Шрёдингера, находящимися в суперпозиции «жив-мёртв». Если в момент t1 наблюдатель А открывает ящик, то его кот равновероятно оказывается либо живым, либо мёртвым. Если живым, то в момент t2 наблюдатель Б открывает свой ящик и находит там мёртвого кота. Проблема в том, что до исходного измерения нет возможности предсказать, у кого именно что окажется, а после один кот жив, другой мёртв, и назад ситуацию не повернуть.
Обход классических ограничений был найден в 2006 году А. Коротковым и Э. Джорданом[53] из Калифорнийского университета за счёт слабых квантовых измерений (англ. weak quantum measurement). Продолжая аналогию, оказалось, что можно не распахивать ящик, а лишь чуть-чуть приподнять его крышку и подсмотреть в щёлку. Если состояние кота неудовлетворительно, то крышку можно сразу захлопнуть и попробовать ещё раз. В 2008 году другая группа исследователей из Калифорнийского университета объявила об успешной экспериментальной проверке данной теории. «Реинкарнация» кота Шрёдингера стала возможной. Наблюдатель А теперь может приоткрывать и закрывать крышку ящика, пока не убедится, что у наблюдателя Б кот окажется в нужном состоянии.[54][55][56]
Открытие возможности «обратного коллапса» во многом перевернуло представления о базовых принципах квантовой механики:
Профессор Влатко Ведрал, Оксфордский университет: «Теперь мы даже не можем сказать, что измерения формируют реальность, — ведь можно элиминировать эффекты замеров и начать всё заново»
Профессор Шлоссхауэр, университет Мельбурна: «Квантовый мир стал ещё более хрупким, а реальность ещё более таинственной».
— Реинкарнация кота Шрёдингера стала возможной. Дата обращения: 15 октября 2011. Архивировано 26 октября 2011 года.
Возникла идея не просто передачи потоков запутанных частиц в разнесённые в пространстве приёмники, но и хранения таких частиц неопределённо долгое время в приёмниках в состоянии суперпозиции для «последующего использования». Ещё из работ Раньяды 1990 года[57] было известно о таких расслоениях Хопфа, которые могли быть топологическими решениями уравнений Максвелла. В переводе на обычный язык это означало, что теоретически (математически) могут существовать ситуации, при которых пучок фотонов или отдельный фотон будет бесконечно циркулировать по сложной замкнутой траектории, выписывая тор в пространстве. До недавнего времени это оставалось просто ещё одной математической абстракцией. В 2008 году американские исследователи занялись анализом получаемых расслоений и их возможной физической реализацией. В результате были найдены[уточнить] стабильные решения. На сентябрь 2011 об успешных лабораторных реализациях не сообщалось, но теперь это вопрос технических трудностей[уточнить], а не физических ограничений[58][59].
Помимо проблемы «складирования» запутанных частиц остаётся нерешённой проблема декогеренции, то есть утраты частицами запутанности со временем из-за взаимодействия с окружающей средой. Даже в физическом вакууме остаются виртуальные частицы, которые вполне успешно деформируют физические тела, как показывает эффект Казимира, и, следовательно, теоретически могут влиять на запутанные частицы.
Квантовая телепортация (не путать с телепортацией), основанная на запутанных квантовых состояниях, используется в таких интенсивно исследуемых областях, как квантовые вычисления и квантовая криптография.
Идея квантовых вычислений была впервые предложена Ю. И. Маниным в 1980 году[60]. На сентябрь 2011 года полномасштабный квантовый компьютер является пока гипотетическим устройством, построение которого связано со многими вопросами квантовой теории и с решением проблемы декогеренции. Ограниченные (в несколько кубитов) квантовые «мини-компьютеры» уже создаются в лабораториях. Первое удачное применение с полезным результатом продемонстрировано международным коллективом учёных в 2009 году. По квантовому алгоритму была определена энергия молекулы водорода[61][62]. Впрочем, некоторыми исследователями высказывается мнение, что для квантовых компьютеров запутанность является, наоборот, нежелательным побочным фактором[63][64].
Квантовая криптография используется для пересылки зашифрованных сообщений по двум каналам связи, квантовому и традиционному. Первый протокол квантового распределения ключа BB84 был предложен[65] Беннетом и Брассардом в 1984 году. С тех пор квантовая криптография являлась одним из бурно развивающихся прикладных направлений квантовой физики, и к 2011 году несколькими лабораториями и коммерческими фирмами были созданы работающие прототипы передатчиков и приёмников[66].
Идея и привлекательность квантовой криптографии базируется не на «абсолютной» криптостойкости, а на гарантированном уведомлении, как только кто-либо попытается перехватить сообщение. Последнее же базируется на известных к началу разработок законах квантовой физики и в первую очередь на необратимости коллапса волновой функции[67]. В связи с открытием и успешным тестированием обратимых слабых квантовых измерений основы надёжности квантовой криптографии оказались под большим вопросом[68][69]. Возможно, квантовая криптография войдёт в историю, как система, для которой прототип «абсолютно надёжного» передатчика и прототип перехватчика сообщений были созданы почти одновременно и до начала практического использования самой системы.
Согласно Хироси Оогури, M. Mарколли и др., квантовая запутанность порождает дополнительные измерения для гравитационной теории. Использование данных о квантовой запутанности в двух измерениях позволяет вычислить плотность вакуумной энергии, которая в трёхмерном пространстве проявляет себя в гравитационном взаимодействии. Это даёт возможность интерпретировать квантовую запутанность как условие, налагаемое на плотность энергии. Эти условия должны удовлетворяться в любой квантовой теории гравитации, согласованной и не противоречащей как ОТО, так и квантовой механике[70][71].
Физическая интерпретация явления
Многомировая интерпретация позволяет[72][73] представить запутанные частицы как проекции всех возможных состояний одной и той же частицы из параллельных вселенных.
Транзакционная интерпретация (TI), предложенная Крамером в 1986 году[74], предполагает наличие исходящих от частиц симметричных стоячих волн, направленных в прошлое и будущее по оси времени. Тогда взаимодействие распространяется по волнам без нарушения лимита скорости света, но для временно́го фрейма наблюдателя событие (транзакция) происходит «мгновенно».
Многочастичная квантовая запутанность
Многочастичная квантовая запутанность — явление квантовой запутанности в квантовой системе, состоящей из трёх и более подсистем или частиц. По сравнению со случаем двух частиц многочастичная квантовая запутанность обладает в общем случае значительно более богатой динамикой. На данный момент многочастичная квантовая запутанность является предметом интенсивного изучения в области квантовой информатики, и является важной составляющей теоретического описания работы квантовых компьютеров.
Квантовая запутанность и кротовые норы
В статье, опубликованной в немецком журнале Fortschritte der Physik в 2013 году, Малдасена и Сасскинд заявили, что червоточина — технически мост Эйнштейна — Розена, или ЭР — является пространственно-временным эквивалентом квантовой запутанности. Это позволило разрешить проблему файервола.[75][76]
Явление в религии и в массовой культуре
Примечания
Литература
- Баргатин И. В., Гришанин Б. А., Задков В. Н. Запутанные квантовые состояния атомных систем // Успехи физических наук : журнал. — М.: Российская академия наук, 2001. — Т. 171, № 6. — doi:10.3367/UFNr.0171.200106c.0625.
- Валиев К. А., Кокин А. А. Квантовые компьютеры: надежды и реальность. — М.: R&C, 2001. — ISBN 5-93972-024-2.
- Килин С. Я. Квантовая информация // Успехи физических наук : журнал. — М.: Российская академия наук, 1999. — Т. 169, № 5. — doi:10.3367/UFNr.0169.199905b.0507.
- Квантовая криптография. Идеи и практика / Под ред. С. Я. Килина, Д. Б. Хорошко, А. П. Низовцева. — Минск: Белорусская наука, 2007. — ISBN 978-985-08-0899-8.
- Нильсен М., Чанг И. Квантовые вычисления и квантовая информация = Quantum Computation and Quantum Information. — М.: Мир, 2006. — ISBN 5-03-003524-9.
- Джордж Массер. Нелокальность. Феномен, меняющий представление о пространстве и времени, и его значение для черных дыр, Большого взрыва и теорий всего = Musser George. Spooky action at a distance. — Альпина Нон-фикшн, 2018. — ISBN 978-5-91671-810-2.
- R. Horodecki, P. Horodecki, M. Horodecki, and K. Horodecki. Quantum entanglement. Rev. Mod. Phys., 81, 865 (2009).
- O. Gühne and G. Tóth. Entanglement detection. Phys. Rep., 474, 1-75 (2009).
- L. Amico, R. Fazio, A. Osterloh, and V. Vedral. Entanglement in many-body systems. Rev. Mod. Phys., 80, 517 (2008).
- Michael Walter, David Gross, Jens Eisert. Multi-partite entanglement (англ.). — 2016. — arXiv:1612.02437.
Ссылки
- Существование объективной реальности вновь поставили под сомнение // Лента.ру, сен 2014
- Физики открыли новый тип квантовой запутанности // Хайтек, янв 2023