Определитель

Определи́тель (детермина́нт) в линейной алгебре — скалярная величина, которая характеризует ориентированное «растяжение» или «сжатие» многомерного евклидова пространства после преобразования матрицей; имеет смысл только для квадратных матриц. Стандартные обозначения определителя матрицы $A$ — $\det(A)$, $|A|$, $\Delta (A)$.

Определитель квадратной матрицы $A$ размеров $n\times n$, заданной над коммутативным кольцом $R$, является элементом кольца $R$. Эта величина определяет многие свойства матрицы $A$, в частности, матрица обратима тогда и только тогда, когда её определитель является обратимым элементом кольца $R$. В случае, когда $R$ — поле, определитель матрицы $A$ равен нулю тогда и только тогда, когда ранг матрицы $A$ меньше $n$, то есть когда системы строк и столбцов матрицы $A$ являются линейно зависимыми.

История

Теория определителей возникла в связи с задачей решения систем линейных уравнений.

К понятию определителя близко подошли авторы древнекитайского учебника «Математика в девяти книгах».

В Европе определители матриц 2 × 2 встречаются у Кардано в XVI веке. Для старших размерностей определение детерминанта дано Лейбницем в 1693 году. Первая публикация принадлежит Крамеру. Теория определителей создана Вандермондом, Лапласом, Коши и Якоби. Термин «определитель» в современном его значении ввёл О. Коши (1815), хотя ранее (1801) «детерминантом» К. Гаусс назвал дискриминант квадратичной формы.

Японский математик Сэки Такакадзу ввёл определители независимо в 1683 году.

Определения

Через перестановки

Для квадратной матрицы $A=(a_{ij})$ размера $n\times n$ её определитель $\det A$ вычисляется по формуле:

$\det A=\sum _{\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}}(-1)^{N(\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})}\cdot a_{1\alpha _{1}}a_{2\alpha _{2}}\dots a_{n\alpha _{n}}$,

где суммирование проводится по всем перестановкам $\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}$ чисел $1,2,\dots ,n$, а $N(\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$ обозначает число инверсий в перестановке $\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}$.

Таким образом, в определитель входит $n!$ слагаемых, которые также называют «членами определителя».

Эквивалентная формула:

$\det A=\sum _{i_{1},i_{2},\ldots ,i_{n}=1}^{n}\varepsilon _{i_{1}i_{2}\dots i_{n}}\cdot a_{1i_{1}}a_{2i_{2}}\dots a_{ni_{n}}$,

где коэффициент $\varepsilon _{i_{1}i_{2}\dots i_{n}}$ — символ Леви-Чивиты — равен:

0, если не все индексы $i_{1},i_{2},\ldots ,i_{n}$ различны,

1, если все индексы $i_{1},i_{2},\ldots ,i_{n}$ различны и подстановка ${\begin{pmatrix}1&2&\dots &n\\i_{1}&i_{2}&\dots &i_{n}\end{pmatrix}}\in S_{n}$ чётна,

−1, если все индексы $i_{1},i_{2},\ldots ,i_{n}$ различны и подстановка ${\begin{pmatrix}1&2&\dots &n\\i_{1}&i_{2}&\dots &i_{n}\end{pmatrix}}\in S_{n}$ нечётна.

Аксиоматическое построение (определение на основе свойств)

Понятие определителя может быть введено на основе его свойств. А именно, определителем вещественной матрицы называется функция $\det :\mathbb {R} ^{n\times n}\rightarrow \mathbb {R}$, обладающая следующими тремя свойствами:

1. $\det(A)$ — кососимметрическая функция строк (столбцов) матрицы $A$.
2. $\det(A)$ — полилинейная функция строк (столбцов) матрицы $A$.
3. $\det(E)=1$, где $E$ — единичная $n\times n$-матрица.

Значение определителя матрицы

Для матрицы первого порядка значение детерминанта равно единственному элементу этой матрицы:

$\Delta ={\begin{vmatrix}a_{11}\end{vmatrix}}=a_{11}$

Матрицы 2 x 2

Схема расчета определителя матрицы 2×2.		Площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма.

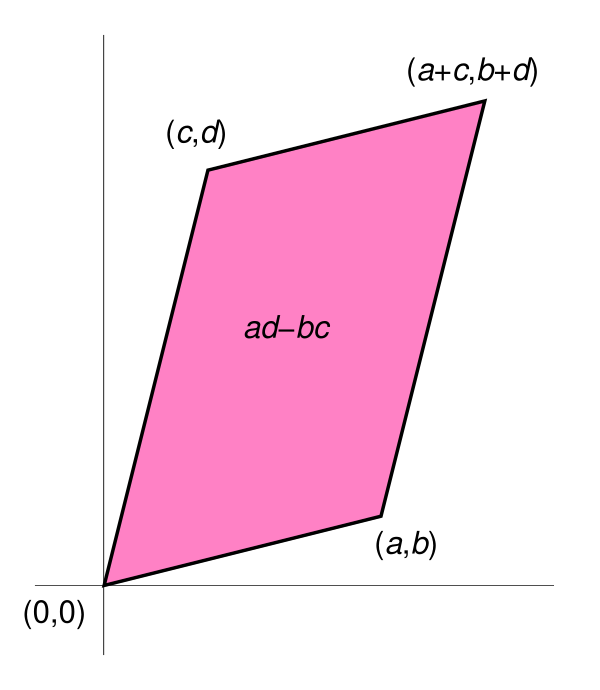
Для матрицы $2\times 2$ определитель вычисляется как:

$\Delta ={\begin{vmatrix}a&c\\b&d\end{vmatrix}}=ad-bc$

Эта матрица A может быть рассмотрена как матрица линейного отображения, преобразующего единичный квадрат в параллелограмм с вершинами (0, 0), (a, b), (a + c, b + d), и (c, d).

Абсолютное значение определителя $|ad-bc|$ равно площади этого параллелограмма, и, таким образом, отражает коэффициент, на который масштабируются площади при преобразовании A.

Значение определителя со знаком (ориентированная площадь параллелограмма) помимо коэффициента масштабирования также показывает, выполняет ли преобразование A отражение.

Матрицы 3 x 3

Определитель матрицы $3\times 3$ можно вычислить по формуле:

$\Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=a_{11}{\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}-a_{12}{\begin{vmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{vmatrix}}+a_{13}{\begin{vmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{vmatrix}}=$

$=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}$

Для более удобного вычисления определителя третьего порядка можно воспользоваться правилом Саррюса или правилом треугольника.

Определитель матрицы, составленной из векторов $\mathbf {a} ,\mathbf {b} ,\mathbf {c}$ равен их смешанному произведению в правой декартовой системе координат и, аналогично двумерному случаю, представляет собой ориентированный объём параллелепипеда, натянутого на $\mathbf {a} ,\mathbf {b} ,\mathbf {c}$. Геометрически определитель матрицы 3х3 означает объем параллелепипеда, построенного на векторах матрицы.

Матрицы N × N

В общем случае, для матриц более высоких порядков (выше 2-го порядка) $n\times n$ определитель можно вычислить, применив следующую рекурсивную формулу:

$\Delta =\sum _{j=1}^{n}(-1)^{1+j}a_{1j}{\bar {M}}_{j}^{1}$, где ${\bar {M}}_{j}^{1}$ — дополнительный минор к элементу $a_{1j}$. Эта формула называется разложением по строке.

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

$\Delta =\sum _{i=1}^{n}(-1)^{i+1}a_{i1}{\bar {M}}_{1}^{i}$

Доказательство

Пусть ${\tilde {\Delta }}=\sum _{i=1}^{n}(-1)^{i+1}a_{i1}{\bar {M}}_{1}^{i}$.

Докажем, что ${\tilde {\Delta }}=\Delta$ по индукции. Видно, что для матрицы $2\times 2$ это верно:

${\tilde {\Delta _{2}}}=\sum _{i=1}^{n}(-1)^{i+1}a_{i1}{\bar {M}}_{1}^{i}=a_{11}a_{22}-a_{21}a_{12}=\Delta _{2}$

Предположим, что для матрицы порядка $n-1$ ${\tilde {\Delta }}_{n-1}=\Delta _{n-1}$ — верно.

${\tilde {\Delta _{n}}}=\sum _{i=1}^{n}(-1)^{i+1}a_{i1}{\bar {M}}_{1}^{i}=a_{11}{\bar {M}}_{1}^{1}+\sum _{i=2}^{n}(-1)^{i+1}a_{i1}{\bar {M}}_{1}^{i}=a_{11}{\bar {M}}_{1}^{1}+\sum _{i=2}^{n}(-1)^{i+1}a_{i1}\sum _{j=2}^{n}(-1)^{j}a_{1j}{\bar {M}}_{1j}^{i1}=$

$=a_{11}{\bar {M}}_{1}^{1}+\sum _{i=2}^{n}\sum _{j=2}^{n}(-1)^{i+j+1}a_{i1}a_{1j}{\bar {M}}_{1j}^{i1}$

${\Delta _{n}}=\sum _{j=1}^{n}(-1)^{1+j}a_{1j}{\bar {M}}_{j}^{1}=a_{11}{\bar {M}}_{1}^{1}+\sum _{j=2}^{n}(-1)^{1+j}a_{1j}{\bar {M}}_{j}^{1}=a_{11}{\bar {M}}_{1}^{1}+\sum _{j=2}^{n}(-1)^{1+j}a_{1j}\sum _{i=2}^{n}(-1)^{i}a_{i1}{\bar {M}}_{j1}^{1i}=$

$=a_{11}{\bar {M}}_{1}^{1}+\sum _{j=2}^{n}\sum _{i=2}^{n}(-1)^{i+j+1}a_{1j}a_{i1}{\bar {M}}_{j1}^{1i}={\tilde {\Delta _{n}}}$ ■

Также справедливо и аналогичное разложение по любой строке (столбцу):

$\Delta =\sum _{j=1}^{n}(-1)^{i+j}a_{ij}{\bar {M}}_{j}^{i}$

Доказательство

Пусть ${\tilde {\Delta }}=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}{\bar {M}}_{j}^{i}$.

Докажем, что ${\tilde {\Delta }}=\Delta$ по индукции. Видно, что для матрицы $2\times 2$ это верно:

${\tilde {\Delta _{2}}}=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}{\bar {M}}_{j}^{i}=-a_{21}a_{12}+a_{22}a_{11}=\Delta _{2}$

Предположим, что для матрицы порядка $n-1$ ${\tilde {\Delta }}_{n-1}=\Delta _{n-1}$ — верно.

${\tilde {\Delta _{n}}}=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}{\bar {M}}_{j}^{i}=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}\left(\sum _{k<j}(-1)^{1+k}a_{1k}{\bar {M}}_{jk}^{i1}+\sum _{k>j}(-1)^{k}a_{1k}{\bar {M}}_{jk}^{i1}\right)$

Соберём коэффициенты при ${\bar {M}}_{j_{0}k_{0}}^{i\,\,1}$:

$j_{0}>k_{0}\colon \;(-1)^{i+j_{0}}a_{ij_{0}}(-1)^{1+k_{0}}a_{1k_{0}}+(-1)^{i+k_{0}}a_{ik_{0}}(-1)^{j_{0}}a_{1j_{0}}=(-1)^{i+j_{0}+k_{0}+1}(a_{ij_{0}}a_{1k_{0}}-a_{ik_{0}}a_{1j_{0}})=$

$=(-1)^{i+j_{0}+k_{0}+1}M_{j_{0}k_{0}}^{1\,\,i}$

$j_{0}<k_{0}\colon \;(-1)^{i+j_{0}}a_{ij_{0}}(-1)^{k_{0}}a_{1k_{0}}+(-1)^{i+k_{0}}a_{ik_{0}}(-1)^{j_{0}+1}a_{1j_{0}}=(-1)^{i+j_{0}+k_{0}+1}(a_{ik_{0}}a_{1j_{0}}-a_{ij_{0}}a_{1k_{0}})=$

$=(-1)^{i+j_{0}+k_{0}+1}M_{j_{0}k_{0}}^{1\,\,i}$

${\tilde {\Delta _{n}}}=\sum _{j\neq k}(-1)^{i+j+k+1}M_{jk}^{1i}{\bar {M}}_{jk}^{1i}$

$\Delta =\sum _{j=1}^{n}(-1)^{1+j}a_{1j}{\bar {M}}_{j}^{1}=\sum _{j=1}^{n}(-1)^{1+j}a_{1j}\left(\sum _{k<j}(-1)^{i+k-1}a_{ik}{\bar {M}}_{jk}^{1i}+\sum _{k>j}(-1)^{i+k-2}a_{ik}{\bar {M}}_{jk}^{1i}\right)$

Соберём коэффициенты при ${\bar {M}}_{j_{0}k_{0}}^{i\,\,1}$:

$j_{0}>k_{0}\colon \;(-1)^{1+j_{0}}a_{1j_{0}}(-1)^{i+k_{0}-1}a_{ik_{0}}+(-1)^{1+k_{0}}a_{1k_{0}}(-1)^{i+j_{0}-2}a_{ij_{0}}=(-1)^{j_{0}+i+k_{0}}(a_{1j_{0}}a_{ik_{0}}-a_{1k_{0}}a_{ij_{0}})=$

$=(-1)^{i+j_{0}+k_{0}+1}M_{j_{0}k_{0}}^{1\,\,i}$

$j_{0}<k_{0}\colon \;(-1)^{1+j_{0}}a_{1j_{0}}(-1)^{i+k_{0}-2}a_{ik_{0}}+(-1)^{1+k_{0}}a_{1k_{0}}(-1)^{i+j_{0}-1}a_{ij_{0}}=(-1)^{k_{0}+i+j_{0}}(a_{1k_{0}}a_{ij_{0}}-a_{1j_{0}}a_{ik_{0}})=$

$=(-1)^{i+j_{0}+k_{0}+1}M_{j_{0}k_{0}}^{1\,\,i}$

${\Delta _{n}}=\sum _{j\neq k}(-1)^{i+j+k+1}M_{jk}^{1i}{\bar {M}}_{jk}^{1i}={\tilde {\Delta _{n}}}$ ■

Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым $k$ строкам (столбцам):

$\Delta =\sum _{1\leqslant j_{1}<\ldots <j_{k}\leqslant n}(-1)^{i_{1}+\ldots +i_{k}+j_{1}+\ldots +j_{k}}M_{j_{1}\ldots j_{k}}^{i_{1}\ldots i_{k}}{\bar {M}}_{j_{1}\ldots j_{k}}^{i_{1}\ldots i_{k}}$

Альтернативные методы вычисления

• Метод конденсации Доджсона, основанный на рекурсивной формуле:

$\Delta ={\frac {{\bar {M}}_{1}^{1}{\bar {M}}_{k}^{k}-{\bar {M}}_{1}^{k}{\bar {M}}_{k}^{1}}{{\bar {M}}_{1,k}^{1,k}}}$.

Основные свойства определителей

Следующие свойства отражают основные результаты теории определителей, применение которых выходит далеко за пределы этой теории:

1. $\det E=1$ (Определитель единичной матрицы равен 1);
2. $\det cA=c^{n}\det A$ (Определитель является однородной функцией степени $n$ на пространстве матриц размера $n\times n$);
3. $\det A^{T}=\det A$ (Определитель матрицы не меняется при её транспонировании);
4. $\det(AB)=\det A\cdot \det B$ (Определитель произведения матриц равен произведению их определителей, $A$ и $B$ — квадратные матрицы одного и того же порядка);
5. $\det A^{-1}=(\det A)^{-1}$, причём матрица $A$ обратима тогда и только тогда, когда обратим её определитель $\det A$;
6. Существует ненулевое решение уравнения $AX=0$ тогда и только тогда, когда $\det A=0$ (или же $\det A$ должен быть нетривиальным делителем нуля в случае, если $R$ — не целостное кольцо).

Определитель как функция строк (столбцов) матрицы

При изучении теории определителей полезно иметь в виду, что в основе этой теории лежит техника манипулирования со строками и столбцами матриц, разработанная К. Ф. Гауссом (преобразования Гаусса). Суть этих преобразований сводится к линейным операциям над строками (столбцами) и их перестановке. Эти преобразования достаточно простым образом отражаются на определителе, и при их изучении удобно «расчленить» исходную матрицу на строки (или столбцы) и считать определитель функцией, определённой над наборами строк (столбцов). Далее буквами ${\hat {A}}_{i}$ обозначаются строки (столбцы) матрицы $A$.

1. Определитель — полилинейная функция строк (столбцов) матрицы. Полилинейность означает линейность функции по каждому аргументу при фиксированных значениях остальных аргументов:

$\det({\hat {A}}_{1},\ldots ,\alpha {\hat {A}}_{i}+\beta {\hat {A'}}_{i},\ldots ,{\hat {A}}_{n})=\alpha \det({\hat {A}}_{1},\ldots ,{\hat {A}}_{i},\ldots ,{\hat {A}}_{n})+\beta \det({\hat {A}}_{1},\ldots ,{\hat {A'}}_{i},\ldots ,{\hat {A}}_{n})$

2. Определитель — кососимметрическая функция строк (столбцов) матрицы, то есть при перестановке двух строк (столбцов) матрицы её определитель умножается на −1:

$\det(\ldots ,{\hat {A}}_{i},\ldots ,{\hat {A}}_{j},\ldots )=-\det(\ldots ,{\hat {A}}_{j},\ldots ,{\hat {A}}_{i},\ldots )$

3. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю:

${\hat {A}}_{i}={\hat {A}}_{j}\Longrightarrow \det(\ldots ,{\hat {A}}_{i},\ldots ,{\hat {A}}_{j},\ldots )=0$

Замечание. Свойства 1-3 являются основными свойствами определителя как функции строк (столбцов), они легко доказываются непосредственно из определения. Свойство 2 (кососимметричность) является логическим следствием свойств 1 и 3. Свойство 3 является логическим следствием свойства 2, если в кольце $R$ элемент 2 (то есть 1 + 1) не совпадает с нулём и не является делителем нуля. Из свойств 1 и 3 вытекают также следующие свойства:

4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя (следствие свойства 1).

5. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю (следствие свойства 4).

6. Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю (следствие свойств 1 и 3).

7. При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится (следствие свойств 1 и 6).

Фактом, имеющим фундаментальное значение, является универсальность определителя как полилинейной кососимметрической функции полного ранга, аргументами которой являются элементы конечномерного векторного пространства $V$ (или $R$-модуля $V$ с конечным базисом). Справедлива следующая

Теорема. Пусть $V$ — свободный $R$-модуль ранга $n$ ($n$-мерное векторное пространство над $R$, если $R$ — поле). Пусть $\varphi (X_{1},X_{2},\dots ,X_{n})$ — $R$-значная функция на $V^{n}$, обладающая свойствами 1-3. Тогда при выборе базиса $E_{1},E_{2},\dots ,E_{n}$ пространства $V$ существует константа $c_{0}=\varphi (E_{1},E_{2},\dots ,E_{n})$ такая, что при всех значениях $X_{1},X_{2},\dots ,X_{n}$ справедливо равенство:

$\varphi (X_{1},X_{2},\dots ,X_{n})=c_{0}\det({\hat {X}}_{1},{\hat {X}}_{2},\dots ,{\hat {X}}_{n})$,

где ${\hat {X}}_{i}$ — столбец координат вектора $X_{i}$ относительно базиса $E_{1},E_{2},\dots ,E_{n}$.

Доказательство

Разложим векторы $X_{1},X_{2},\dots ,X_{n}$ по базису $E_{1},E_{2},\dots ,E_{n}$: $X_{i}=\sum _{j=1}^{n}x_{ij}E_{j}$. Тогда им будут соответствовать следующие столбцы: ${\hat {X}}_{i}=\sum _{j=1}^{n}x_{ij}{\hat {E}}_{j}$.

В силу полилинейности функции $\varphi$ $\varphi (X_{1},X_{2},\dots ,X_{n})=\varphi (\sum _{i_{1}=1}^{n}x_{1i_{1}}E_{i_{1}},\sum _{i_{2}=1}^{n}x_{2i_{2}}E_{i_{2}},\dots ,\sum _{i_{n}=1}^{n}x_{ni_{n}}E_{i_{n}})=\sum _{i_{1},i_{2},\dots ,i_{n}=1}^{n}\varphi (E_{i_{1}},E_{i_{2}},\dots ,E_{i_{n}})\cdot x_{1i_{1}}x_{2i_{2}}\dots x_{ni_{n}}$

В силу свойства 3, если среди индексов $i_{1},i_{2},\dots ,i_{n}$ есть совпадающие, то

$\varphi (E_{i_{1}},E_{i_{2}},\dots ,E_{i_{n}})=0$.

В противном случае, в силу кососимметричности (свойства 2), получается:

$\varphi (E_{i_{1}},E_{i_{2}},\dots ,E_{i_{n}})=\varepsilon _{i_{1}i_{2}\dots i_{n}}\varphi (E_{1},E_{2},\dots ,E_{n})$.

Таким образом, $\varphi (X_{1},X_{2},\dots ,X_{n})=c_{0}\det({\hat {X}}_{1},{\hat {X}}_{2},\dots ,{\hat {X}}_{n})$, где $c_{0}=\varphi (E_{1},E_{2},\dots ,E_{n})$. ■

Одним из важнейших следствий универсальности определителя является следующая теорема о мультипликативности определителя.

Теорема. Пусть $A$ — матрица размера $n\times n$. Тогда $\det(AX)=\det A\cdot \det X$ для любой матрицы $X$ размера $n\times n$.

Доказательство

Рассмотрим на пространстве столбцов $R^{n}$ кососимметрическую полилинейную форму $\varphi ({\hat {X}}_{1},{\hat {X}}_{2},\dots ,{\hat {X}}_{n})=\det(A{\hat {X}}_{1},A{\hat {X}}_{2},\dots ,A{\hat {X}}_{n})=\det(AX)$. Согласно доказанной теореме, эта форма равна $c_{0}\det({\hat {X}}_{1},{\hat {X}}_{2},\dots ,{\hat {X}}_{n})=c_{0}\det X$, где $c_{0}=\varphi (E_{1},E_{2},\dots ,E_{n})=\det({\hat {A}}_{1},{\hat {A}}_{2},\dots ,{\hat {A}}_{n})=\det A$. ■

Определитель и ориентированный объём

Пусть ${\vec {a}},{\vec {b}},{\vec {c}}$ — три вектора в пространстве $\mathbb {R} ^{3}$. Они порождают параллелепипед, вершины которого лежат в точках с радиус-векторами ${\vec {0}},{\vec {a}},{\vec {b}},{\vec {c}},{\vec {a}}+{\vec {b}},{\vec {c}}+{\vec {a}},{\vec {b}}+{\vec {c}},{\vec {a}}+{\vec {b}}+{\vec {c}}$. Этот параллелепипед может быть вырожден, если вектора ${\vec {a}},{\vec {b}},{\vec {c}}$ компланарны (лежат в одной плоскости, линейно зависимы).

Функция ориентированного объёма ${\rm {Vol}}({\vec {a}},{\vec {b}},{\vec {c}})$ определяется как объём параллелепипеда, порождённого этими векторами, и взятый со знаком «+», если тройка векторов $({\vec {a}},{\vec {b}},{\vec {c}})$ положительно ориентирована, и со знаком «-», если она ориентирована отрицательно. Функция ${\rm {Vol}}({\vec {a}},{\vec {b}},{\vec {c}})$ полилинейна и кососимметрична. Свойство 3, очевидно, выполнено. Для доказательства полилинейности этой функции, достаточно доказать её линейность по вектору ${\vec {a}}$. Если вектора ${\vec {b}},{\vec {c}}$ линейно зависимы, значение ${\rm {Vol}}({\vec {a}},{\vec {b}},{\vec {c}})$ будет нулевым независимо от вектора ${\vec {a}}$, и значит, линейно зависящим от него. Если вектора ${\vec {b}},{\vec {c}}$ линейно независимы, обозначим через ${\vec {n}}$ вектор единичной нормали к плоскости векторов ${\vec {b}},{\vec {c}}$, такой, что ${\rm {Vol}}({\vec {n}},{\vec {b}},{\vec {c}})>0$. Тогда ориентированный объём параллелепипеда равен произведению площади основания, построенного на векторах ${\vec {b}},{\vec {c}}$ и независящего от вектора ${\vec {a}}$, и алгебраической величины проекции вектора ${\vec {a}}$ на нормаль к основанию, которая равна скалярному произведению $\langle {\vec {a}},{\vec {n}}\rangle$ и является величиной, линейно зависящей от вектора ${\vec {a}}$. Линейность по ${\vec {a}}$ доказана, и аналогично доказывается линейность по остальным аргументам.

Применяя теорему об универсальности определителя как кососимметрической полилинейной функции, получаем, что при выборе ортонормированного базиса $({\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3})$ пространства $\mathbb {R} ^{3}$

${\rm {Vol}}({\vec {a}},{\vec {b}},{\vec {c}})={\rm {Vol}}({\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3})\det {\begin{pmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{pmatrix}}=\det {\begin{pmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{pmatrix}}$,

где $a_{i},b_{i},c_{i}$ — координаты векторов $({\vec {a}},{\vec {b}},{\vec {c}})$ в выбранном базисе.

Таким образом, определитель матрицы коэффициентов векторов относительно ортонормированного базиса имеет смысл ориентированного объёма параллелепипеда, построенного на этих векторах.

Всё вышесказанное без существенных изменений переносится на пространство $\mathbb {R} ^{n}$ произвольной размерности.

Разложение определителя по строке/столбцу и обращение матриц

Формулы разложения определителя по строке/столбцу позволяют сводить вычисление определителей к рекурсивной процедуре, использующей вычисление определителей меньших порядков. Для вывода этих формул сгруппируем и просуммируем в формуле для определителя матрицы $C=(c_{ij})$, с учётом равенства $\varepsilon _{i_{1}\dots i_{n-1}n}=\varepsilon _{i_{1}\dots i_{n-1}}$, все ненулевые члены, содержащие элемент $c_{nn}$. Эта сумма равна:

$c_{nn}\sum _{i_{1},\dots i_{n-1}=1}^{n-1}\varepsilon _{i_{1}\dots i_{n-1}n}c_{1i_{1}}\dots c_{n-1,i_{n-1}}=c_{nn}\sum _{i_{1},\dots i_{n-1}=1}^{n-1}\varepsilon _{i_{1}\dots i_{n-1}}c_{1i_{1}}\dots c_{n-1,i_{n-1}}=c_{nn}\det C_{n}^{n}$,

где $C_{i}^{j}$ — матрица, получаемая из $C$ удалением строки с номером $i$ и столбца с номером $j$.

Так как произвольный элемент $c_{ij}$ можно $(n-j)$ перестановками соответствующего столбца вправо и $(n-i)$ перестановками соответствующей строки вниз переместить в правый нижний угол матрицы, причём дополнительная к нему матрица сохранит свой вид, то сумма всех членов в разложении определителя, содержащих $c_{ij}$, будет равна

$(-1)^{(n-i)}(-1)^{(n-j)}c_{ij}\det C_{i}^{j}=(-1)^{i+j}c_{ij}\det C_{i}^{j}=c_{ij}A_{i}^{j}$.

Величина $A_{i}^{j}=(-1)^{i+j}\det C_{i}^{j}$ называется алгебраическим дополнением элемента матрицы $c_{ij}$.

Учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из i-ой строки, можно разложить определитель по членам этой строки:

$\det C=\sum _{j=1}^{n}c_{ij}A_{i}^{j}$ — Формула разложения определителя по i-ой строке

Аналогично, учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из j-го столбца, можно разложить определитель по членам этого столбца:

$\det C=\sum _{i=1}^{n}c_{ij}A_{i}^{j}$ — Формула разложения определителя по j-ому столбцу

Если элементы k-й строки матрицы $C$ скопировать в i-ую строку, её определитель станет равен нулю, а по формуле разложения определителя по i-ой строке получится:

$0=\sum _{j=1}^{n}c_{kj}A_{i}^{j}$ — Формула «фальшивого» разложения определителя по i-ой строке ($i\neq k$).

Аналогично для столбцов:

$0=\sum _{j=1}^{n}c_{ik}A_{i}^{j}$ — Формула «фальшивого» разложения определителя по j-ому столбцу ($j\neq k$)

Полученные формулы полезно записать в матричном виде. Введём матрицу алгебраических дополнений к элементам матрицы $C$: $A=(A_{i}^{j})$. Тогда, согласно с полученными формулами,

$CA^{T}=A^{T}C=(\det C)\cdot E$.

Следствие 1 (Критерий обратимости матриц). Квадратная матрица $C$ является обратимой тогда и только тогда, когда $\det C$ — обратимый элемент кольца $R$, при этом $C^{-1}=(\det C)^{-1}\cdot A^{T}$.

Следствие 2. Если произведение матриц равно нулю $CX=0$, и матрица $C$ — квадратная, тогда $(\det C)\cdot X=0$.

Решение систем линейных алгебраических уравнений с помощью определителей

Формула Крамера позволяет выразить решение системы линейных алгебраических уравнений в виде отношения определителей, в знаменателе которого стоит определитель системы, а в числителе — определитель матрицы системы, в которой столбец коэффициентов при соответствующей переменной заменён на столбец из правых частей уравнений.

Формула Крамера. Пусть задана система линейных алгебраических уравнений в матричном виде: $CX=B$, где $C=(c_{ij})$ — матрица коэффициентов системы размера $n\times n$, $B=(b_{1},b_{2},\dots ,b_{n})^{T}$ — столбец из правых частей уравнений системы, и вектор $X=(x_{1},x_{2},\dots ,x_{n})^{T}$ — решение этой системы. Тогда при любых $\lambda _{1},\lambda _{2},\dots ,\lambda _{n}\in R$ справедливо равенство:

$(\lambda _{1}x_{1}+\lambda _{2}x_{2}+\dots +\lambda _{n}x_{n})\cdot (\det C)=-\det {\begin{pmatrix}c_{11}&c_{12}&\dots &c_{1n}&b_{1}\\c_{21}&c_{22}&\dots &c_{2n}&b_{2}\\\dots &\dots &\dots &\dots &\dots \\c_{n1}&c_{n2}&\dots &c_{nn}&b_{n}\\\lambda _{1}&\lambda _{2}&\dots &\lambda _{n}&0\end{pmatrix}}$

Доказательство

Обозначим через $\Lambda X$ сумму $\lambda _{1}x_{1}+\lambda _{2}x_{2}+\dots +\lambda _{n}x_{n}$ и введём

матрицу $D={\begin{pmatrix}c_{11}&c_{12}&\dots &c_{1n}&b_{1}\\c_{21}&c_{22}&\dots &c_{2n}&b_{2}\\\dots &\dots &\dots &\dots &\dots \\c_{n1}&c_{n2}&\dots &c_{nn}&b_{n}\\\lambda _{1}&\lambda _{2}&\dots &\lambda _{n}&\Lambda X\end{pmatrix}}$ и вектор $X'={\begin{pmatrix}x_{1}\\x_{2}\\\dots \\x_{n}\\-1\end{pmatrix}}$.

Тогда $DX'=0$ и согласно следствию 2 из предыдущего раздела $(\det D)X'=0$.

Но так как одна из компонент вектора $X'$ равна -1, это означает, что $\det D=0$. Утверждение доказано, так как

$\det D=\Lambda X\cdot (\det C)+\det {\begin{pmatrix}c_{11}&c_{12}&\dots &c_{1n}&b_{1}\\c_{21}&c_{22}&\dots &c_{2n}&b_{2}\\\dots &\dots &\dots &\dots &\dots \\c_{n1}&c_{n2}&\dots &c_{nn}&b_{n}\\\lambda _{1}&\lambda _{2}&\dots &\lambda _{n}&0\end{pmatrix}}$ ■

Из этой формулы следует, в частности, что если $\det C$ — не вырожден (не является нулём или делителем нуля), система может обладать не более чем одним решением, а если определитель ещё и обратим, то система обладает единственным решением.

Одной из важнейших теорем в теории определителей является следующая теорема о решениях однородной системы линейных уравнений.

Теорема. Пусть $R$ — поле. Однородная система линейных уравнений $CX=0$ имеет нетривиальное (ненулевое) решение тогда и только тогда, когда определитель матрицы коэффициентов равен нулю: $\det C=0$.

Доказательство

Необходимость условия содержится в следствии 2 предыдущего раздела. Докажем необходимость.

Если матрица $C$ — нулевая, любой вектор $X$ является решением. Пусть $C_{0}$ — максимальный невырожденный минор в матрице $C$ имеет размеры $r\times r$. Не ограничивая общности, считаем, что этот минор образован первыми r строками и столбцами (иначе перенумеруем переменные и переставим уравнения в другом порядке.) Введём вектора $X_{0}=(x_{1},x_{2},\dots ,x_{r})^{T}$ и $X_{1}=(x_{r+1},\dots ,x_{n})^{T}$. Тогда первые r уравнений системы в матричном виде записываются так:

$C_{0}X_{0}+C_{1}X_{1}=0$

Поскольку матрица $C_{0}$ обратима, любому значению $X_{1}$ соответствует единственный вектор $X_{0}=-C_{0}^{-1}C_{1}X_{1}$, удовлетворяющий этим уравнениям. Покажем, что при этом остальные уравнения будут выполнены автоматически. Пусть $j>r$.

Введём две матрицы:

$D_{1}={\begin{pmatrix}c_{11}&\dots &c_{1r}&c_{1r+1}x_{r+1}+\dots +c_{1n}x_{n}\\c_{21}&\dots &c_{2r}&c_{2r+1}x_{r+1}+\dots +c_{2n}x_{n}\\\dots &\dots &\dots &\dots \dots \dots \dots \\c_{r1}&\dots &c_{rr}&c_{rr+1}x_{r+1}+\dots +c_{rn}x_{n}\\c_{j1}&\dots &c_{jr}&c_{jr+1}x_{r+1}+\dots +c_{jn}x_{n}\\\end{pmatrix}}$ и $D_{2}={\begin{pmatrix}c_{11}&\dots &c_{1r}&c_{1r+1}x_{r+1}+\dots +c_{1n}x_{n}\\c_{21}&\dots &c_{2r}&c_{2r+1}x_{r+1}+\dots +c_{2n}x_{n}\\\dots &\dots &\dots &\dots \dots \dots \dots \\c_{r1}&\dots &c_{rr}&c_{rr+1}x_{r+1}+\dots +c_{rn}x_{n}\\c_{j1}&\dots &c_{jr}&-(c_{j1}x_{1}+\dots +c_{jr}x_{r})\\\end{pmatrix}}$.

У матрицы $D_{1}$ все столбцы являются частями столбцов из матрицы $C$, а последний столбец есть линейная комбинация столбцов матрицы $C$ с коэффициентами $x_{r+1},\dots ,x_{n}$, поэтому в силу линейности определителя по столбцам $\det D_{1}$ есть линейная комбинация определителей миноров матрицы $C$ размера $(r+1)\times (r+1)$. Так как $C_{0}$ — максимальный по размеру невырожденный минор, все миноры большего размера имеют нулевой определитель, поэтому $\det D_{1}=0$.

Из соотношения $C_{0}X_{0}+C_{1}X_{1}=0$ следует, что $D_{2}Y=0$, где столбец $Y=(x_{1},\dots ,x_{r},1)^{T}\neq 0$. Поэтому $\det D_{2}=0$.

Тогда $0=\det D_{1}-\det D_{2}=(\det C_{0})\cdot (c_{j1}x_{1}+c_{j2}x_{2}+\dots +c_{jn}x_{n})$. И так как $\det C_{0}\neq 0$, то j-ое уравнение системы тоже выполнено. ■

Данная теорема используется, в частности, для нахождения собственных значений и собственных векторов матриц.

Критерий полноты и линейной независимости системы векторов

Тесно связанными с понятием определителя является понятие линейной зависимости и полноты систем векторов в векторном пространстве.

Пусть $R$ — поле, $V$ — векторное пространство над $R$ с конечным базисом ${\vec {e_{1}}},{\vec {e_{2}}},\dots ,{\vec {e_{n}}}$. Пусть задан ещё набор из $n$ векторов ${\vec {v_{1}}},{\vec {v_{2}}},\dots ,{\vec {v_{n}}}$. Их координатами $v_{ij}$ относительно заданного базиса являются коэффициенты разложения ${\vec {v_{i}}}=\sum v_{ij}{\vec {e_{j}}}$. Составим (квадратную) матрицу $A=(v_{ij})$. Справедлива теорема:

Теорема (Критерий полноты и линейной независимости системы векторов).

(1) Система векторов ${\vec {v_{1}}},{\vec {v_{2}}},\dots ,{\vec {v_{n}}}$ линейно зависима тогда и только тогда, когда $\det A=0$.

(2) Система векторов ${\vec {v_{1}}},{\vec {v_{2}}},\dots ,{\vec {v_{n}}}$ полна, тогда и только тогда, когда матрица $A$ не вырождена ($\det A\neq 0$).

Доказательство

(1) Доказательство основано на том, что вектор $\sum x_{i}{\vec {v_{i}}}$ имеет столбец координат, равный $AX$, где $X=(x_{1},x_{2},\dots ,x_{n})^{T}$.

Если $\sum x_{i}{\vec {v_{i}}}=0$, то $AX=0$. Тогда $(\det A)\cdot X=0$ и если $X$ отличен от нуля, то $\det A=0$.

Обратно, если $\det A=0$, существует ненулевой столбец $X$, такой что $AX=0$. Это означает, что $\sum x_{i}{\vec {v_{i}}}=0$.

(2) Если матрица $A$ не вырождена, она обратима. Пусть ${\vec {u}}$ — произвольный вектор, $Y=(y_{1},y_{2},\dots ,y_{n})^{T}$ — столбец его координат, $X=A^{-1}Y=(x_{1},x_{2},\dots ,x_{n})^{T}$. Тогда ${\vec {u}}=\sum x_{i}{\vec {v_{i}}}$. Таким образом, произвольный вектор разложим по системы векторов ${\vec {v_{1}}},{\vec {v_{2}}},\dots ,{\vec {v_{n}}}$, что означает её полноту.

Обратно, пусть матрица $A$ вырождена. Тогда существует ненулевая строка коэффициентов $C=(c_{1},c_{2},\dots ,c_{n})$, такая, что $CA=0$. Это значит, что любой вектор ${\vec {u}}=\sum x_{i}{\vec {v_{i}}}$, разложимый по системе векторов ${\vec {v_{1}}},{\vec {v_{2}}},\dots ,{\vec {v_{n}}}$, удовлетворяет ограничению $c_{1}x_{1}+c_{2}x_{2}+\dots +c_{n}x_{n}=0$. Если какой-то коэффициент $c_{k}$ отличен от нуля, то базисный вектор ${\vec {e_{k}}}$ не разложим по этой системе векторов, и значит, она не полна. ■

Следствие. В векторном пространстве $V$, обладающем конечным базисом из $n$ векторов:

(1) всякая система, состоящая менее, чем из $n$ векторов, не полна;

(2) всякая система, состоящая более, чем из $n$ векторов, линейно зависима;

(3) всякий базис пространства $V$ содержит ровно $n$ векторов.

Таким образом, размерность векторного пространства $V$ с конечным базисом корректно определена.

Некоторые специальные свойства определителей

• Определитель матрицы равен произведению её собственных значений.
• Если квадратная матрица выражает линейное преобразование, то её определитель не меняется при замене базиса линейного пространства.

Алгоритмическая реализация

• Прямые методы вычисления определителя могут быть основаны непосредственно на его определении, как суммы по перестановкам, или на разложении Лапласа по определителям меньшего порядка. Однако такие методы очень неэффективны, так как требуют О(n!) операций для вычисления определителя $n$-го порядка. В то же время они универсальны, применимы в тех случаях, когда элементы матрицы не являются числами (функции, многочлены, дифференциальные формы чётной степени и т. д.), и не требуют выполнения операций деления.
• Можно вычислить определитель и выполнив меньшее количество операций умножения; точнее, можно для матрицы $n\times n$ обойтись лишь количеством слагаемых, равным количеству разбиений числа $n$ вместо $n!$, например 5 вместо 6 для $3\times 3$:

  ${\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=(a_{11}+a_{12})(a_{21}+a_{23})(a_{31}+a_{32})-a_{12}a_{21}(a_{31}+a_{32}+a_{33})-a_{13}(a_{21}+a_{22}+a_{23})a_{31}-(a_{11}+a_{12}+a_{13})a_{23}a_{32}+a_{11}a_{22}a_{33}$.

• Один из наиболее быстрых численных методов вычисления определителя заключается в простой модификации метода Гаусса. Следуя методу Гаусса, произвольную матрицу $A$ можно привести к ступенчатому виду (Верхнетреугольная матрица), используя лишь две следующие операции над матрицей — перестановку двух строк и добавление к одной из строк матрицы другой строки, умноженной на произвольное число. Из свойств определителя следует, что вторая операция не изменяет определителя матрицы, а первая лишь меняет его знак на противоположный. Определитель матрицы, приведённой к ступенчатому виду, равен произведению элементов на её диагонали, так как она является треугольной, поэтому определитель исходной матрицы равен:

  $\det A=(-1)^{s}\cdot \det A_{\mbox{ref}},$

где $s$ — число перестановок строк, выполненных алгоритмом, а $A_{\mbox{ref}}$ — ступенчатая форма матрицы $A$, полученная в результате работы алгоритма. Сложность этого метода, как и метода Гаусса, составляет $O(n^{3})$, для его реализации необходимо использование операции деления.

• Определитель можно вычислить, зная LU-разложение матрицы. Если $A=LU$, где $L$ и $U$ — треугольные матрицы, то $\det A=(\det L)(\det U)$. Определитель треугольной матрицы равен просто произведению её диагональных элементов.
• Если доступен алгоритм, выполняющий умножение двух матриц порядка $n$ за время $M(n)$, где $M(n)\geqslant n^{a}$, для некоторого $a>2$, то определитель матрицы порядка $n$ может быть вычислен за время $O(M(n))$. В частности это означает, что, используя для умножения матриц алгоритм Копперсмита — Винограда, определитель можно вычислить за время $O(n^{2.376})$.

Специальные виды определителей

• Определитель Вронского (Вронскиан)
• Определитель Вандермонда
• Определитель Грама
• Определитель Якоби (Якобиан)

См. также

• Циркулянт
• Перманент
• Пфаффиан
• Результант

Литература

• В. А. Ильин, Э. Г. Позняк Линейная алгебра, М.: Наука — Физматлит, 1999.
• Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2000.
• Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры: Учебник для вузов. М.: Физматлит, 2004.
• Боревич З. И. Определители и матрицы. — М.: Наука, 1988.