Кеплер, Иоганн
Иога́нн Ке́плер (нем. Johannes Kepler; 27 декабря 1571 года, Вайль-дер-Штадт — 15 ноября 1630 года, Регенсбург) — немецкий математик, астроном, механик, оптик, первооткрыватель законов движения планет Солнечной системы.
Именем Кеплера назван космический орбитальный телескоп НАСА[4].
Что важно знать
| Иоганн Кеплер | |
|---|---|
| Johannes Kepler | |
| Имя при рождении | нем. Johannes Kepler |
| Дата рождения | 27 декабря 1571[1] |
| Место рождения | Вайль-дер-Штадт, Священная Римская империя |
| Дата смерти | 15 ноября 1630[2][1][…] (58 лет) |
| Место смерти | Регенсбург |
| Страна | Священная Римская империя |
| Научная сфера | астрономия, математика, механика, физика |
| Место работы | |
| Образование | |
| Учёная степень | бакалавр искусств[2] (1588) и магистр искусств[2] (1591) |
| Научный руководитель | Мёстлин, Михаэль |
| Ученики | Петер Крюгер, Ambrosius Rhode[d][3] и Johann Odontius[d][3] |
| Известен как | автор Законов движения планет |
| Автограф |
|
Биография
Иоганн Кеплер родился в имперском городе Вайль-дер-Штадте (в 30 километрах от Штутгарта, сейчас — федеральная земля Баден-Вюртемберг). Его отец, Генрих Кеплер, служил наёмником в Испанских Нидерландах. Когда юноше было 18 лет, отец отправился в очередной поход и исчез навсегда. Мать Кеплера, Катарина Кеплер, содержала трактир, подрабатывала гаданием и траволечением[5].
Интерес к астрономии появился у Кеплера ещё в детские годы, когда его мать показала впечатлительному мальчику яркую комету (1577), а позднее — лунное затмение (1580). После перенесённой в детстве оспы Кеплер получил пожизненный дефект зрения, который мешал ему проводить астрономические наблюдения, однако любовь к астрономии он сохранил навсегда[6].
В 1589 году Кеплер окончил школу при монастыре Маульбронн, проявив выдающиеся способности[7]. Городские власти назначили ему стипендию для помощи в дальнейшем обучении. В 1591 году поступил в университет в Тюбингене — сначала на факультет искусств, к которым тогда причисляли и математику с астрономией, затем перешёл на теологический факультет. Здесь он впервые услышал (от Михаэля Мёстлина) о разработанной Николаем Коперником гелиоцентрической системе мира и стал её сторонником[8]. Университетским другом Кеплера был Кристоф Безольд, будущий правовед.
Первоначально Кеплер планировал стать протестантским священником, но благодаря незаурядным математическим способностям был приглашён в 1594 году читать лекции по математике в университете города Граца (ныне в Австрии).
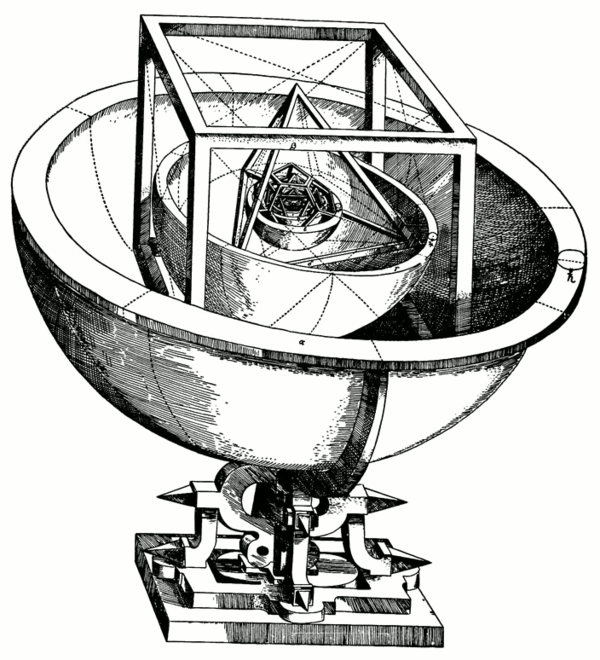
В Граце Кеплер провёл 6 лет. Здесь вышла в свет (1596) его первая книга «Тайна мироздания» (Mysterium Cosmographicum). В ней Кеплер попытался найти тайную гармонию Вселенной, для чего сопоставил орбитам пяти известных тогда планет (сферу Земли он выделял особо) различные «платоновы тела» (правильные многогранники). Орбиту Сатурна он представил как круг (ещё не эллипс) на поверхности шара, описанного вокруг куба. В куб, в свою очередь, был вписан шар, который должен был представлять орбиту Юпитера. В этот шар был вписан тетраэдр, описанный вокруг шара, представлявшего орбиту Марса и т. д. Эта работа после дальнейших открытий Кеплера утратила своё первоначальное значение (хотя бы потому, что орбиты планет оказались не круговыми); тем не менее, в наличие скрытой математической гармонии Вселенной Кеплер верил до конца жизни, и в 1621 году переиздал «Тайну мира», внеся в неё многочисленные изменения и дополнения[9].
Книгу «Тайна мироздания» Кеплер послал Галилею и Тихо Браге. Галилей одобрил гелиоцентрический подход Кеплера, хотя мистическую нумерологию не поддержал. В дальнейшем они вели оживлённую переписку, и это обстоятельство (общение с «еретиком»-протестантом) на суде над Галилеем было особо подчёркнуто как отягчающее вину Галилея[10].
Тихо Браге, как и Галилей, отверг надуманные построения Кеплера, однако высоко оценил его знания, оригинальность мысли и пригласил Кеплера к себе.
В 1597 году Кеплер женился на вдове Барбаре Мюллер фон Мулек. Их первые двое детей умерли во младенчестве, а жена заболела эпилепсией. В довершение невзгод, в католическом Граце начались гонения на протестантов[11]. Кеплер, занесённый в список изгоняемых «еретиков», был вынужден покинуть город и принять приглашение Тихо Браге. Сам Браге к этому времени был выселен из своей обсерватории и переехал в Прагу, где служил у императора Рудольфа II придворным астрономом и астрологом.
В 1600 году оба изгнанника — Кеплер и Браге — встретились в Праге. Проведённые здесь 10 лет — самый плодотворный период жизни Кеплера.
Вскоре выяснилось, что взгляды Коперника и Кеплера на астрономию Тихо Браге разделял только отчасти. Чтобы сохранить геоцентризм, Браге предложил компромиссную модель: все планеты, кроме Земли, вращаются вокруг Солнца, а Солнце вращается вокруг неподвижной Земли (гео-гелиоцентрическая система мира). Эта теория получила большую известность и в течение нескольких десятилетий являлась основным конкурентом системы мира Коперника[12].
После смерти Браге в 1601 году Кеплер стал его преемником в должности. Казна императора из-за нескончаемых войн была постоянно пуста, жалованье Кеплеру платили редко и скудно. Он вынужден был подрабатывать составлением гороскопов. Кеплеру пришлось также вести многолетнюю тяжбу с наследниками Тихо Браге, которые пытались отобрать у него, среди прочего имущества покойного, также и результаты астрономических наблюдений. В конце концов, от них удалось откупиться[13].
В 1604 году Кеплер опубликовал свои наблюдения сверхновой, называемой теперь его именем.
Будучи великолепным наблюдателем, Тихо Браге за много лет составил объёмный труд по наблюдению планет и сотен звёзд, причём точность его измерений была существенно выше, чем у всех предшественников. Для повышения точности Браге применял как технические усовершенствования, так и специальную методику нейтрализации погрешностей наблюдения. Особо ценной была систематичность измерений[14].
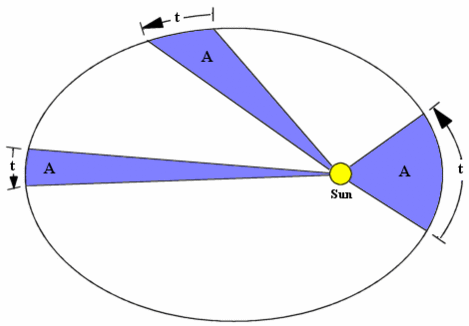
На протяжении нескольких лет Кеплер внимательно изучал данные Браге и в результате тщательного анализа пришёл к выводу, что траектория движения Марса представляет собой не круг, а эллипс, в одном из фокусов которого находится Солнце — положение, известное сегодня как первый закон Кеплера. Анализ привёл и ко второму закону (фактически второй закон был открыт даже раньше первого): радиус-вектор, соединяющий планету и Солнце, в равное время описывает равные площади. Это означало, что чем дальше планета от Солнца, тем медленнее она движется.
Законы Кеплера были сформулированы Кеплером в 1609 году в книге «Новая астрономия», причём, осторожности ради, он относил их только к Марсу[15].
Новая модель движения вызвала огромный интерес среди учёных-коперниканцев, хотя не все они её приняли. Галилей кеплеровы эллипсы решительно отверг[16]. После смерти Кеплера Галилей заметил в письме: «Я всегда ценил ум Кеплера — острый и свободный, пожалуй, даже слишком свободный, но способы мышления у нас совсем разные»[17].
В 1610 году Галилей сообщил Кеплеру об открытии спутников Юпитера. Кеплер встретил это сообщение недоверчиво и в полемической работе «Разговор со Звёздным вестником» привёл несколько юмористическое возражение: «непонятно, к чему быть [спутникам], если на этой планете нет никого, кто бы мог любоваться этим зрелищем»[18]. Но позже, получив свой экземпляр телескопа, Кеплер изменил своё мнение, подтвердил наблюдение спутников и сам занялся теорией линз. Результатом стали усовершенствованный телескоп и фундаментальная работа «Диоптрика».
В Праге у Кеплера родились два сына и дочь. В 1611 году старший сын Фридрих умер от оспы. В это же время душевнобольной император Рудольф II, проиграв войну с собственным братом Матвеем, отрёкся в его пользу от чешской короны и вскоре умер[19]. Кеплер начал сборы для переезда в Линц, но тут после долгой болезни умерла его жена Барбара.
В 1612 году, собрав скудные средства, Кеплер переехал в Линц, где прожил 14 лет. За ним была сохранена должность придворного математика и астронома, но в деле оплаты новый император оказался ничем не лучше старого. Некоторый доход приносили преподавание и гороскопы.
В 1613 году Кеплер женился на 24-летней дочери столяра Сусанне. У них родилось семеро детей, выжили четверо[20].
В 1615 году Кеплер получает известие, что его мать обвинена в колдовстве. Кеплер пишет городским властям; мать вначале отпускают, но затем снова арестовывают. Следствие тянулось 5 лет. Наконец, в 1620 году начался суд. Кеплер сам выступил защитником, и через год измученную женщину, наконец, освободили. В следующем году она скончалась[21].
Тем временем Кеплер продолжал астрономические исследования и в 1618 году открыл третий закон: отношение куба среднего удаления планеты от Солнца к квадрату периода обращения её вокруг Солнца есть величина постоянная для всех планет:
- a3/T2 = const.
Этот результат Кеплер публикует в завершающей книге «Гармония мира», причём применяет его уже не только к Марсу, но и ко всем прочим планетам (включая, естественно, и Землю), а также к галилеевым спутникам[22].
Отметим, что в книге, наряду с ценнейшими научными открытиями, изложены также философские рассуждения о «музыке сфер» и платоновых телах, которые составляют, по мнению учёного, эстетическую суть высшего проекта мироздания.
В 1626 году в ходе Тридцатилетней войны Линц был осаждён и вскоре захвачен. Начались грабежи и пожары; в числе прочих сгорела типография. Кеплер переехал в Ульм и в 1628 году перешёл на службу к Валленштейну.
В 1630 году Кеплер отправился к императору в Регенсбург, чтобы получить хотя бы часть жалованья. По дороге сильно простудился и вскоре умер.
После смерти Кеплера наследникам досталось: поношенная одежда, 22 флорина наличными, 29000 флоринов невыплаченного жалованья, 27 опубликованных рукописей и множество неопубликованных; они позже были изданы в 22-томном сборнике[5].
Со смертью Кеплера его злоключения не закончились. В конце Тридцатилетней войны было полностью разрушено кладбище, где он похоронен, и от его могилы ничего не осталось. Часть архива Кеплера исчезла. В 1774 году бо́льшую часть архива (18 томов из 22) по рекомендации Леонарда Эйлера приобрела Петербургская Академия наук[23], сейчас хранится в Санкт-Петербургском филиале архива РАН[24].
Научная деятельность
Альберт Эйнштейн назвал Кеплера «несравненным человеком» и писал о его судьбе[25]:
Он жил в эпоху, когда ещё не было уверенности в существовании некоторой общей закономерности для всех явлений природы. Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и не понятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения!
Сейчас, когда эти законы уже установлены, трудно себе представить, сколько изобретательности, воображения и неустанного, упорного труда потребовалось, чтобы установить эти законы и со столь огромной точностью выразить их.
В конце XVI века в астрономии ещё происходила борьба между геоцентрической системой Птолемея и гелиоцентрической системой Коперника. Противники системы Коперника ссылались на то, что в отношении погрешности расчётов она ничем не лучше птолемеевской. Напомним, что в модели Коперника планеты равномерно движутся по круговым орбитам: чтобы согласовать это предположение с видимой неравномерностью движения планет, Копернику пришлось ввести дополнительные движения по эпициклам. Хотя эпициклов у Коперника было меньше, чем у Птолемея, его астрономические таблицы, первоначально более точные, чем птолемеевы, вскоре существенно разошлись с наблюдениями, что немало озадачило и охладило восторженных коперниканцев.
Открытые Кеплером три закона движения планет полностью и с превосходной точностью объяснили видимую неравномерность этих движений. Вместо многочисленных надуманных эпициклов модель Кеплера включает только одну кривую — эллипс. Второй закон установил, как меняется скорость планеты при удалении или приближении к Солнцу, а третий позволяет рассчитать эту скорость и период обращения вокруг Солнца.
Хотя исторически кеплеровская система мира основана на модели Коперника, фактически у них очень мало общего (только суточное вращение Земли). Исчезли круговые движения сфер, несущих на себе планеты, появилось понятие планетной орбиты. В системе Коперника Земля всё ещё занимала несколько особое положение, поскольку центром мира Коперник объявил центр земной орбиты. У Кеплера Земля — рядовая планета, движение которой подчинено общим трём законам. Все орбиты небесных тел — эллипсы (движение по гиперболической траектории открыл позднее Ньютон), общим фокусом орбит является Солнце.
Кеплер вывел также «уравнение Кеплера», используемое в астрономии для определения положения небесных тел.
Законы планетной кинематики, открытые Кеплером, послужили позже Ньютону основой для создания теории тяготения. Ньютон математически доказал, что все законы Кеплера являются прямыми следствиями закона тяготения.
Взгляды Кеплера на устройство Вселенной за пределами Солнечной системы вытекали из его мистической философии. Солнце он полагал неподвижным, а сферу звёзд считал границей мира. В бесконечность Вселенной Кеплер не верил и в качестве аргумента предложил (1610) то, что позже получило название фотометрический парадокс: если число звёзд бесконечно, то в любом направлении взгляд наткнулся бы на звезду, и на небе не существовало бы тёмных участков[26][27].
Строго говоря, система мира Кеплера претендовала не только на выявление законов движения планет, но и на гораздо большее. Аналогично пифагорейцам, Кеплер считал мир реализацией некоторой числовой гармонии, одновременно геометрической и музыкальной; раскрытие структуры этой гармонии дало бы ответы на самые глубокие вопросы[28][29]:
Я выяснил, что все небесные движения, как в их целом, так и во всех отдельных случаях, проникнуты общей гармонией, правда, не той, которой я предполагал, но ещё более совершенной.
Оригинальный текст (лат.)[показатьскрыть]Totam Harmonices naturam, quantaquanta est, cum omnibus suis partibus, libro III. explicatis, inter Motus cœlestes reperiri; non eo quidem modo, quem ego conceperam animo; pars hæc est non postrema mei gaudij; sed diversissimo alio, simulque & præstantissimo & perfectissimo.
Например, Кеплер объясняет, почему планет именно шесть (к тому времени были известны только шесть планет Солнечной системы) и они размещены в пространстве так, а не как-либо иначе: оказывается, орбиты планет вписаны в правильные многогранники. Интересно, что исходя из этих ненаучных соображений, Кеплер предсказал существование двух спутников Марса и промежуточной планеты между Марсом и Юпитером.
Законы Кеплера соединяли в себе ясность, простоту и вычислительную мощь, однако мистическая форма его системы мира основательно засоряла реальную суть великих открытий Кеплера. Тем не менее, уже современники Кеплера убедились в точности новых законов, хотя их глубинный смысл до Ньютона оставался непонятным. Никаких попыток реанимировать модель Птолемея или предложить иную систему движения, кроме гелиоцентрической, больше не предпринималось.
Кеплер немало сделал для принятия протестантами григорианского календаря (на сейме в Регенсбурге, 1613, и в Ахене, 1615).
Кеплер стал автором первого обширного (в трёх томах) изложения коперниканской астрономии (Epitome Astronomiae Copernicanae, 1617—1622), которое немедленно удостоилось чести попасть в «Индекс запрещённых книг». В эту книгу, свой главный труд, Кеплер включил описание всех своих открытий в астрономии.
Летом 1627 года Кеплер после 22 лет трудов опубликовал (за свой счёт[30]) астрономические таблицы, которые в честь императора назвал «Рудольфовыми». Спрос на них был огромен, так как все прежние таблицы давно разошлись с наблюдениями. Немаловажно, что труд впервые включал удобные для расчётов таблицы логарифмов. Кеплеровы таблицы служили астрономам и морякам вплоть до начала XIX века[5].
Через год после смерти Кеплера Гассенди наблюдал предсказанное им прохождение Меркурия по диску Солнца[31]. В 1665 году итальянский физик и астроном Джованни Альфонсо Борелли опубликовал книгу, где законы Кеплера подтверждаются для открытых Галилеем спутников Юпитера.
Кеплер нашёл способ определения объёмов разнообразных тел вращения, который описал в книге «Новая стереометрия винных бочек» (1615). Предложенный им метод содержал первые элементы интегрального исчисления[32]. Позднее Кавальери использовал тот же подход для разработки исключительно плодотворного «метода неделимых». Завершением этого процесса стало открытие математического анализа.
Кроме того, Кеплер очень подробно проанализировал симметрию снежинок. Исследования по симметрии привели его к предположениям о плотной упаковке шаров, согласно которым наибольшая плотность упаковки достигается при пирамидальном упорядочивании шаров друг над другом[33]. Математически доказать этот факт не удавалось на протяжении 400 лет — первое сообщение о доказательстве гипотезы Кеплера появилось лишь в 1998 году в работе математика Томаса Хейлса. Пионерские работы Кеплера в области симметрии нашли позже применение в кристаллографии и теории кодирования.
В ходе астрономических исследований Кеплер внёс вклад в теорию конических сечений. Он составил одну из первых таблиц логарифмов[34].
У Кеплера впервые встречается термин «среднее арифметическое»[35].
Кеплер вошёл и в историю проективной геометрии: он впервые ввёл важнейшее понятие бесконечно удалённой точки[36]. Он же ввёл понятие фокуса конического сечения и рассмотрел проективные преобразования конических сечений, в том числе меняющие их тип — например, переводящие эллипс в гиперболу.
Именно Кеплер ввёл в физику термин инерция как прирождённое свойство тел сопротивляться приложенной внешней силе. Заодно он, как и Галилей, формулирует в ясном виде первый закон механики: всякое тело, на которое не действуют иные тела, находится в покое или совершает равномерное прямолинейное движение[37].
Кеплер вплотную подошёл к открытию закона тяготения, хотя и не пытался выразить его математически. Он писал в книге «Новая астрономия», что в природе существует «взаимное телесное стремление сходных (родственных) тел к единству или соединению». Источником этой силы, по его мнению, является магнетизм в сочетании с вращением Солнца и планет вокруг своей оси[38].
В другой книге Кеплер уточнил[38][39]:
Гравитацию я определяю как силу, подобную магнетизму — взаимному притяжению. Сила притяжения тем больше, чем оба тела ближе одно к другому.
Оригинальный текст (лат.)[показатьскрыть]Gravitatem ego definio virtute, magneticæ simili, attractionis mutuæ. Hujus verò attractionis major vis est in corporibus inter se vicinis, quàm in remotis.
Правда, Кеплер ошибочно полагал, что эта сила распространяется только в плоскости эклиптики. Видимо, он считал, что сила притяжения обратно пропорциональна расстоянию (а не квадрату расстояния); впрочем, его формулировки недостаточно ясны.
Кеплер первый, почти на сто лет раньше Ньютона, выдвинул гипотезу о том, что причиной приливов является воздействие Луны на верхние слои океанов[40].
В 1604 году Кеплер издал содержательный трактат по оптике «Дополнения к Вителлию», а в 1611 году — ещё одну книгу, «Диоптрика». С этих трудов начинается история оптики как науки[41]. В этих сочинениях Кеплер подробно излагает как геометрическую, так и физиологическую оптику. Он описывает преломление света, рефракцию и понятие оптического изображения, общую теорию линз и их систем. Вводит термины «оптическая ось» и «мениск», впервые формулирует закон падения освещённости обратно пропорционально квадрату расстояния до источника света. Впервые описывает явление полного внутреннего отражения света при переходе в менее плотную среду.
Описанный им физиологический механизм зрения, с современных позиций, принципиально верен. Кеплер выяснил роль хрусталика, верно описал причины близорукости и дальнозоркости.
Глубокое проникновение в законы оптики привело Кеплера к схеме телескопической подзорной трубы (телескоп Кеплера), изготовленной в 1613 году Кристофом Шайнером. К 1640-м годам такие трубы вытеснили в астрономии менее совершенный телескоп Галилея.
Кеплер и астрология
Отношение Кеплера к астрологии было двойственным. С одной стороны, он допускал, что земное и небесное находятся в некоем гармоничном единстве и взаимосвязи. С другой — скептически оценивал возможность использовать эту гармонию для предсказания конкретных событий.
Кеплер говорил: «Люди ошибаются, думая, что от небесных светил зависят земные дела»[42]. Широко известно также другое его откровенное высказывание[43][44]:
Конечно, эта астрология глупая дочка; но, Боже мой, куда бы делась её мать, высокомудрая астрономия, если бы у неё не было глупенькой дочки! Свет ведь ещё гораздо глупее и так глуп, что для пользы этой старой разумной матери глупая дочь должна болтать и лгать. И жалованье математиков (Mathematicorum salaria) так ничтожно, что мать наверное бы голодала, если бы дочь ничего не зарабатывала.
Оригинальный текст (нем.)[показатьскрыть]Es ist wol diese Astrologia ein närrisches Töchterlin … aber lieber Gott/wo wolt jhr Mutter die hochvernünfftige Astronomia bleiben/wann sie diese Jhre närrische Tochter nit hette/ist doch die Welt noch viel närrischer/und so närrisch/daß deroselben zu jhren selbst frommen diese alte verständige Mutter die Astronomia durch der Tochter Narrentaydung/weil sie zumal auch einen Spiegel hat/nur eyngeschwärzt und eyngelogen werden muß. Und seynd sonsten die Mathematicorum salaria so seltzam und so gering/daß die Mutter gewißlich Hunger leyden müste/wann die Tochter nichts erwürbe.
Тем не менее, Кеплер не порывал с астрологией никогда. Более того, он имел свой собственный взгляд на природу астрологии, чем выделялся среди астрологов-современников. В труде «Гармония мира» он утверждает, что «в небесах нет светил, приносящих несчастья», но человеческая душа способна «резонировать» с лучами света, исходящими от небесных тел, она запечатлевает в памяти конфигурацию этих лучей в момент своего рождения. Сами же планеты, в представлении Кеплера, были живыми существами, наделёнными индивидуальной душой[45].
Благодаря некоторым удачным предсказаниям Кеплер заработал репутацию искусного астролога. В Праге одной из его обязанностей было составление гороскопов для императора. Следует заметить, вместе с тем, что Кеплер при этом не занимался астрологией исключительно ради заработка и составлял гороскопы для себя и своих близких. Так в своей работе «О себе» он приводит описание собственного гороскопа, а когда в январе 1598 года у него родился сын, Генрих, Кеплер составил гороскоп и для него. По его мнению, ближайшим годом, когда жизни его сына угрожала опасность, был 1601 год, но сын умер уже в апреле 1598 года.
Попытки Кеплера составить гороскоп для полководца Валленштейна также далеко разошлись с реальностью. В 1608 году Кеплер составил гороскоп полководцу, в котором предрекал женитьбу на 33-м году жизни, называл опасными для жизни годы 1613, 1625 и 70-й год жизни Валленштейна, а также описал ряд других событий. Когда стало очевидно, что предсказания потерпели неудачу. Валленштейн вернул гороскоп Кеплеру, который, исправив в нём время рождения на полчаса, получил точное соответствие между предсказанием и течением жизни. Однако и этот вариант содержал промахи. Так, Кеплер полагал, что период с 1632 по 1634 год будет благополучным для полководца, и не сулит опасности. Но в феврале 1634 года Валленштейн был убит.
Память
В честь И. Кеплера были названы:
- Кеплер — ударный кратер на Луне
- Кеплер — ударный кратер на Марсе
- (1134) Кеплер — астероид
- Сверхновая Кеплера — сверхновая звезда № 1604 , описанная им.
- Кеплер (телескоп) — орбитальная обсерватория НАСА, выведена на орбиту в 2009 году для поиска и исследования планет за пределами Солнечной системы.
- Университет в Линце.
- Keplerplatz — площадь и станция метро в городе Вена[46].
- Иоганн Кеплер (ATV) — Европейский грузовой космический корабль, 2011 года.
В Вайль-дер-Штадте[47], Праге (см. Музей Кеплера), Граце[48] и Регенсбурге функционируют музеи Кеплера.
Другие мероприятия в память о Кеплере:
- В 1971 году к 400-летию со дня рождения Кеплера в ГДР была выпущена памятная монета достоинством 5 марок.
- В 2009 году к 400-летию открытия Кеплеровских законов в Германии выпущена памятная серебряная монета достоинством 10 евро.
Жизни учёного посвящены художественные произведения:
- Опера и симфония «Гармония мира» композитора Пауля Хиндемита (1956 год).
- Историческая повесть Юрия Медведева «Капитан звёздного океана (Кеплер)», Молодая гвардия, 1972.
- Художественный фильм «Иоганнес Кеплер» режиссёра Франка Фогеля (ГДР, 1974 год).
- Роман Джона Бэнвилла Кеплер, переведённый на русский язык в 2008 году.
- Опера «Кеплер» композитора Филипа Гласса (2009 год).
- Художественный фильм «Глаз астронома» режиссёра Стэна Ньюманна (Франция, 2012 год).
- Опера «Суд Кеплера» композитора Тима Уаттса (2016 год).
Марки в честь 400-летнего юбилея Кеплера (1971)
Труды Кеплера
- Mysterium cosmographicum (Тайна мироздания), 1596
- De Fundamentis Astrologiae Certioribus (О более достоверных основаниях астрологии), 1601
- Astronomiae Pars Optica (Оптика в астрономии), 1604
- Ad Vitellionem paralipomena (Дополнения к Вителлию), физиологическая оптика, 1604
- De Stella nova in pede Serpentarii (О новой звезде в созвездии Змееносца), 1604
- Astronomia nova (Новая астрономия), 1609
- Tertius Interveniens (Третий промежуточный), 1610
- Dissertatio cum Nuncio Sidereo (Разговор со Звёздным вестником), полемика со «Звёздным вестником» Галилея, 1610
- Dioptrice (Диоптрика), 1611
- De nive sexangula (О шестиугольных снежинках), 1611
- De vero Anno, quo aeternus Dei Filius humanam naturam in Utero benedictae Virginis Mariae assumpsit (Об истинном годе, когда вечный Сын Божий воспринял человеческую природу от Пресвятой Девы Марии), 1613
- Eclogae Chronicae, 1615
- Nova stereometria doliorum vinariorum (Новая стереометрия винных бочек), 1615
- Epitome Astronomiae Copernicanae (Коперниканская астрономия, в 3-х томах), 1618—1621
- Harmonices Mundi (Гармония мира), 1619
- Mysterium cosmographicum (Тайна мира, 2-е изд.), 1621
- Tabulae Rudolphinae (Рудольфовы таблицы), 1627
- Somnium («Сон, или Посмертное сочинение о лунной астрономии», фантастический рассказ о полёте на Луну), 1634
- Библиография научных работ Кеплера с ссылками на оригиналы
- Кеплер, Иоганн. Новая стереометрия винных бочек. — М.—Л.: ГТТИ, 1935. — 360 с.
- Кеплер, Иоганн. О шестиугольных снежинках. Сон. Разговор с Звёздным вестником. . — М.: Наука, 1982.
- Разговор с звёздным вестником по изд.: И. Кеплер, О шестиугольных снежинках, М., Наука, 1982.
- Сон, или Посмертное сочинение о лунной астрономии по изд.: И. Кеплер, О шестиугольных снежинках, М., Наука, 1982.
Примечания
Литература
- Белонучкин В. Е. Кеплер, Ньютон и всё-всё-всё. М.: Наука, Серия Библиотечка «Квант», выпуск 78, 1990. 128 с.
- Белый Ю. А. Иоганн Кеплер. — М.: Наука, 1971. — 295 с. — 17 000 экз.
- Белый Ю. А. Вклад Кеплера в развитие математики и его астрономические исследования // Историко-астрономические исследования. Вып. XI. 1972. С. 65—106.
- Бондаренко С. Б. Путь к славе Иоганна Кеплера // Философия науки. — 2016. — № 4. — С. 146—175.
- Бэнвилл, Джон. Кеплер. — Текст, 2008. — 288 с. — (Первый ряд). — ISBN 978-5-7516-0711-1.
- Веселовский И. Н. Кеплер и Галилей // Историко-астрономические исследования. Вып. XI. 1972. С. 19—64.
- Данилов Ю. А. Гармония и астрология в трудах Кеплера] // Прекрасный мир науки. — Традиция, 2008. — 383 с. — ISBN 5-89826-282-2.
- Еремеева А. И., Цицин Ф. А. История астрономии. — М.: Изд-во МГУ, 1989.
- История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Кеплер, Иоганн // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Колчинский И. Г., Корсунь А. А., Родригес М. Г. Астрономы: Биографический справочник. — 2-е изд., перераб. и доп.. — Киев: Наукова думка, 1986. — 512 с.
- Коперник, Галилей, Лаплас, Эйлер, Кетле. Биографические повествования (библиотека Ф. Павленкова). Челябинск, «Урал», 1997.
- Линник В. П. Труды Кеплера в области оптики // Историко-астрономические исследования. Вып. XII. 1975. С. 89—100.
- Лишевский В. П. Рассказы об учёных. М.: Наука, 1986, с. 14—30.
- Лопес, Эдуардо Баттанер. Танцы со звёздами. Кеплер. Движение планет // Наука. Величайшие теории. — М.: Де Агостини, 2015. — Вып. 4. — ISSN 2409-0069.
- Паули В. Влияние архетипических представлений на формирование естественнонаучных теорий у Кеплера // Паули В. Физические очерки. Сб. статей. М., 1975. С. 137—174.
- Филоненко В. С. Кеплер и парадокс Ольберса // Земля и Вселенная. — 1984. — № 2. — С. 63.
- Храмов Ю. А. Кеплер Иоганн (Kepler Johannes) // Физики : Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и доп. — Москва : Наука, 1983. — С. 130. — 400 с. — 200 000 экз.
- Applebaum W. Keplerian Astronomy after Kepler: Researches and Problems. History of Science, 1996, V. 34, p. 451—504.
- Caspar, Max. Kepler. — New York: Dover, 1993. — ISBN 0-486-67605-6.
- Gingerich O. Kepler, Johannes. Complete Dictionary of Scientific Biography.
- Koyre A. The Astronomical Revolution. New York: Dover, 1973.
- Voelkel J. R. Kepler, Johannes. Complete Dictionary of Scientific Biography.
Ссылки
- Kepler’s discovery (анимации на тему «Новой астрономии» Кеплера)
- Daniel A. Di Liscia. «Johannes Kepler» (Stanford Encyclopedia of Philosophy) (англ.)
- Johannes Kepler’s New Astronomy (англ.)
- Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Johannes Kepler (англ.) — биография в архиве MacTutor.
- Davis A. E. L.. «Kepler’s Planetary Laws» (англ.)