Оптимизация (математика)

Задачи оптимизации делятся на два типа в зависимости от того, являются ли переменные непрерывными или дискретными:

• Если переменные дискретны, задача называется дискретной оптимизацией, при этом требуется найти объект, например целое число, перестановка или граф, из счётного множества.
• Если переменные непрерывны, задача относится к непрерывной оптимизации, где оптимальные значения ищутся среди элементов непрерывного множества. Такие задачи могут содержать ограничения и быть мультимодальными.

Задачу оптимизации можно записать так:

Дано: функция ${\displaystyle f:A\rightarrow \mathbb {R} }$ из некоторого множества A в вещественные числа;

Требуется: найти элемент x₀ ∈ A такой, что f(x₀) ≤ f(x) для всех x ∈ A (минимизация) или f(x₀) ≥ f(x) для всех x ∈ A (максимизация).

Такую формулировку называют задачей оптимизации или задачей математического программирования (последний термин не связан напрямую с программированием, но широко применяется, например, в линейном программировании — см. раздел История.) Во многих прикладных и теоретических задачах можно воспользоваться этим общим подходом.

Поскольку справедливо равенство

${\displaystyle f(\mathbf {x} _{0})\geq f(\mathbf {x} )\Leftrightarrow -f(\mathbf {x} _{0})\leq -f(\mathbf {x} ),}$

достаточно рассматривать только минимизационные задачи — максимизационные можно привести к ним через смену знака функции цели.

В физике такие задачи часто называют минимизацией энергии^[5], трактуя значение функции f как энергию системы в заданной модели. В машинном обучении качество модели непрерывно оценивается с помощью функции потерь; её минимум соответствует оптимальному набору параметров.

Обычно A — это подмножество евклидова пространства ${\displaystyle \mathbb {R} ^{n}}$, заданное системой ограничений — равенствами и неравенствами, которым должны удовлетворять допустимые решения. Это множество A называют пространством поиска или множеством допустимых решений, а его элементы — кандидатными решениями или физибильными решениями.

Функция f называется по-разному: функция цели, критериальная функция, функция потерь, функция затрат (при минимизации)^[6], функция полезности или функция приспособленности (при максимизации), а также энергетическая функция или энергетический функционал в ряде научных дисциплин. Физибильное решение, минимизирующее (или максимизирующее) целевую функцию, называется оптимальным решением.

В математике стандартные задачи оптимизации обычно формулируются как задачи минимизации.

Локальный минимум x* — это такой элемент, что существует δ > 0, удовлетворяющий

${\displaystyle \forall \,\mathbf {x} \in A\;{\text{при}}\;\left\Vert \mathbf {x} -\mathbf {x} ^{*}\right\Vert \leq \delta \,}$

выполняется неравенство f('x*) ≤ f(x).

Иначе говоря, в окрестности точки x* функция не принимает меньших значений. Локальные максимумы определяются аналогично.

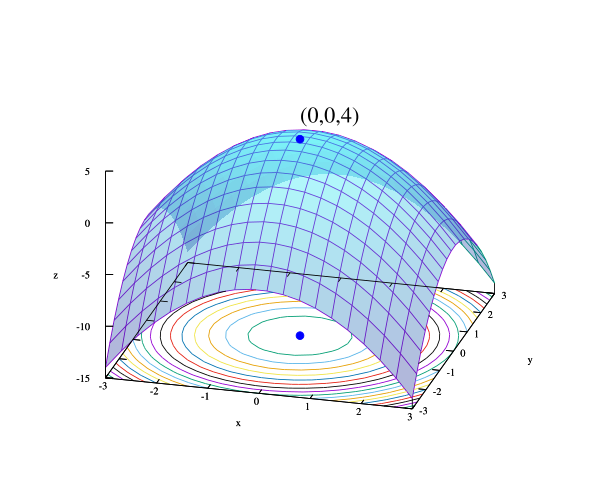
Локальный минимум не обязательно глобален — если функция не выпукла в задаче минимизации, могут существовать несколько локальных минимумов. В выпуклой задаче локальный минимум внутри области допустимых решений всегда глобален, а в невыпуклой — их может быть много и все они не обязаны быть глобальными.

Большинство алгоритмов для невыпуклых задач, в том числе и коммерческие пакеты, не отличают глобальные оптимальные решения от локальных и могут выдать локальный минимум как результат. Глобальная оптимизация — отдельная ветвь прикладной математики и численных методов, занимающаяся построением алгоритмов, гарантирующих сходимость к глобальному оптимуму за конечное число шагов.

Задачи оптимизации часто записывают в специальной форме. Например:

Рассмотрим запись:

${\displaystyle \min _{x\in \mathbb {R} }\;(x^{2}+1)}$

Она означает минимальное значение целевой функции x² + 1 при выборе x из множества вещественных чисел ${\displaystyle \mathbb {R} }$. В этом случае минимум равен 1, достигается при {{{1}}}.

Аналогично,

${\displaystyle \max _{x\in \mathbb {R} }\;2x}$

означает поиск максимального значения функции 2x, где x — любое вещественное число. Максимум не существует, так как функция неограниченна — ответ «бесконечность» или «не определено».

Запись

${\displaystyle {\underset {x\in (-\infty ,-1]}{\operatorname {arg\,min} }}\;x^{2}+1}$

или эквивалентно

${\displaystyle {\underset {x}{\operatorname {arg\,min} }}\;x^{2}+1,\;{\text{при}}\;x\in (-\infty ,-1]}$

означает те значения аргумента x из промежутка (−∞,−1] которые минимизируют функцию x² + 1 (само минимальное значение не спрашивается). В данном случае ответ — {{{1}}}, так как {{{1}}} не принадлежит допустимому множеству.

Аналогично,

${\displaystyle {\underset {x\in [-5,5],\;y\in \mathbb {R} }{\operatorname {arg\,max} }}\,x\cos y}$

или эквивалентно

${\displaystyle {\underset {x,\,y}{\operatorname {arg\,max} }}\,x\cos y,\;{\text{при}}\;x\in [-5,5],\;y\in \mathbb {R} }$

означает нахождение пар {x, y} максимизирующих x\cos y, при дополнительном условии x ∈ [-5, 5]. Решения — пары {5, 2k\pi} и {–5, (2k + 1)\pi}, где k пробегает все целые числа.

Операторы arg min и arg max иногда также записываются слитно: argmin и argmax, и обозначают «аргумент минимума» и «аргумент максимума».

Ферма и Лагранж вывели формулы поиска экстремумов с помощью анализа, Ньютон и Гаусс предложили итерационные методы приближения к оптимуму.

Термин «линейное программирование» для ряда задач оптимизации принадлежит Джорджу Б. Данцигу, хотя теоретическая база была заложена ранее, в частности Леонидом Канторовичем в 1939 году. («Программирование» в данном случае не связано с компьютерным программированием, а происходит от военной терминологии — обозначения расписаний подготовки и снабжения.) Данциг опубликовал симплекс-метод в 1947 году, а также фон Нейман и другие учёные в это же время исследовали теорию линейного программирования (например, двойственность)^[7].

К видным учёным-теоретикам в области оптимизации относятся:

• Выпуклое программирование — частный случай, когда целевая функция выпукла (минимизация) или вогнута (максимизация), а множество ограничений образует выпуклое множество. Это либо частный случай нелинейного программирования, либо обобщение линейного и выпуклого квадратичного программирования.
  • Линейное программирование (ЛП) — частный вид выпуклого программирования, где функция цели линейна, а ограничения — только линейные равенства/неравенства (множество решений образует многогранник или многогранное тело, если оно ограничено).
  • Вторично-конусное программирование — выпуклый случай, включает некоторые типы квадратичных задач.
  • Полуопределённое программирование — частная область выпуклой оптимизации, задачи в которой формулируются с полуопределёнными матрицами.
  • Конусное программирование — обобщённая форма выпуклого программирования. ЛП, SOCP и SDP — подвиды конусных задач по соответствующему типу конусов.
  • Геометрическое программирование — техника, позволяющая сводить задачи, где функции ограничений выражаются через позиномиалы и мониомы, к выпуклым.
• Целочисленное программирование — задачи линейного программирования с дополнительным ограничением: переменные принимают только целые значения. Это невыпуклый, и, как правило, более сложный для вычислений класс задач.
• Квадратичное программирование — функция цели содержит квадратные члены, множество решений — с линейными ограничениями. При определённых условиях задача выпуклая.
• Фракционное программирование — оптимизация отношения двух нелинейных функций; отдельный класс выпуклых фракционных задач может быть сведён к выпуклой оптимизации.
• Нелинейное программирование — наиболее общий случай: нелинейность может содержаться как в целевой функции, так и в ограничениях. Выпуклая или невыпуклая природа задачи определяет, насколько она труднорешаема.
• Стохастическое программирование — часть ограничений или параметров моделируются как случайные величины.
• Робастная оптимизация — моделирование неопределённости в данных задачи, построение решений, устойчивых к различным сценариям из множества неопределённости.
• Комбинаторная оптимизация — решения выбираются из дискретного (или сводимого к таковому) множества.
• Стохастическая оптимизация используется при наличии случайных шумов в измерениях функции или входных данных.
• Бесконечномерная оптимизация — класс задач, где допустимое множество решений — бесконечномерное пространство, например, пространство функций.
• Эвристические методы и метаэвристики — делают минимальные предположения о свойствах задачи и зачастую не гарантируют поиск глобального оптимального решения, но применяются для приближённых решений сложных задач.
• Задача удовлетворения ограничений — частный случай, когда функция цели постоянна (в используется в искусственном интеллекте, автоматизированном выводе).

• • Внутри задач удовлетворения ограничений выделяют программирование с ограничениями — подход, в котором между переменными задаются ограничения, а не функции цели.
• Дизъюнктивное программирование — задачи, где достаточно выполнения по крайней мере одного ограничения из набора.
• Space mapping — концепция моделирования и оптимизации инженерных систем с использованием грубых (коarse) и точных (fine) моделей.

Части методов лежат в области динамической оптимизации (принятие решений с течением времени):

• Вариационное исчисление — поиск экстремумов функционалов, например, поверхности наименьшей площади при заданной границе.
• Оптимальное управление — обобщение вариационного исчисления с вводом управляющих воздействий.
• Динамическое программирование — метод разбиения задачи на подзадачи (ключевое уравнение — уравнение Беллмана).
• Математическое программирование с равновесными ограничениями — ограничения содержат вариационные неравенства или комплементарные условия.

Добавление нескольких критериев приводит к необходимости поиска компромисса — например, при проектировании конструкции требуется минимизировать массу и одновременно увеличить жёсткость. Класс решений, которые улучшают один критерий только за счёт ухудшения другого, называется множеством Парето, а соответствующая кривая — граница Парето.

Решение считается оптимальным по Парето, если оно не доминируется никаким другим (то есть не уступает другому по всем критериям и превосходит по какому-то одному). Выбор между решениями на множестве Парето осуществляется лицом, принимающим решение, и отражает дополнительные предпочтения, которые явным образом не указаны в задаче.

Многокритериальные задачи обобщаются до векторной оптимизации, где частичный порядок может быть шире, чем порядок Парето.

Часто задачи оптимизации мультимодальны — имеют несколько «хороших» решений (глобальных или локальных экстремумов). Их задача — получение хотя бы некоторой части этих решений.

Классические методы (градиентные, итерационные) редко находят разные экстремумы при разных начальных условиях, поэтому для поиска всех решений обычно применяют методы глобальной оптимизации: эволюционные алгоритмы, байесовскую оптимизацию, метод имитации отжига и др.

Задача достижимости допустимого множества (или задача удовлетворимости) является частным случаем оптимизации, где значениями функции цели не интересуются вовсе, а требуется найти хоть одно допустимое решение.

Многие алгоритмы оптимизации начинают с поиска физибильной точки — иногда за счёт введения вспомогательных переменных (слэк/потенциал), проигрывая их до устранения всех ограничений.

Теорема Вейерштрасса утверждает: непрерывная вещественная функция на компакте достигает максимума и минимума. Более общий вариант: нижнеполунепрерывная функция на компакте достигает минимума; верхнеполунепрерывная — максимума.

Теорема Ферма: экстремумы неконстреинтных задач достигаются в стационарных точках, где первая производная или градиент функции цели равны нулю (см. признак первого порядка). В иных случаях — в критических точках, где производная не существует, либо на границе допустимого множества. Описание этих условий называют условиями первого порядка.

Для задач с равенствами ограничения используются множители Лагранжа, а при наличии и равенств, и неравенств — условия Каруша-Куна-Такера.

Признак первого порядка выделяет экстремальные точки, но не отличает минимум от максимума или седловой точки. При наличии вторых производных используются матрица Гессе (неконстреинтные) или её модификации (бордированная) — признак второго порядка (метод второго порядка для экстремума).

Теорема об огибающей описывает, как меняется значение оптимального решения при изменении параметров (раздел сравнительная статика).

Теорема Берже о максимуме (1963) описывает непрерывность оптимальных решений как функции параметров.

Для неконстреинтных задач с дважды дифференцируемыми функциями критические точки ищутся как места, где градиент равен нулю. Для выпуклых функций и локально липшицевых функций наличие нулевого субградиента означает достижение локального минимума. Модификация (положительно-отрицательный момент) может ускорить реальную сходимость к глобальному минимуму^[8].

Тип критической точки анализируется через определённость матрицы Гессе: если она положительно определена — точка локальный минимум, отрицательно определена — максимум, не определена — седловая точка.

Констреинтные задачи сводят к неконстреинтным с помощью множителей Лагранжа; метод лагранжева релаксация позволяет находить приближённые решения трудных задач.

Если функция цели выпуклая, то локальный минимум всегда глобален. Для таких задач существуют эффективные численные методы, например методы внутренней точки.

Если функция цели не квадратична, то используются иные схемы сходимости: линейный поиск (поиск вдоль расписания), доверительная область. Оба подхода распространены в современных методах недифференцируемой оптимизации. Обычно глобальный оптимизатор медленнее локального (например, BFGS), поэтому иногда строят гибридные методы.

Практически задачи решают с помощью:

• алгоритмов, завершающихся за конечное число шагов;
• итерационных методов, сходящихся к решению для всего класса задач;
• эвристик, дающих приближённые решения (без гарантии сходимости).

• Симплекс-метод Данцига, предназначен для линейного программирования
• Обобщения симплекс-метода для квадратичного программирования и линейно-фракционного программирования
• Варианты симплекс-метода, адаптированные для сетевой оптимизации
• Комбинаторные алгоритмы
• Квантовые алгоритмы оптимизации

Выбор итерационного метода для нелинейных задач зависит от того, используются ли градиент, матрица Гессе или только значения функции. Использование Гессе и градиентов ускоряет сходимость, но увеличивает вычислительную сложность каждого шага.

Главный критерий эффективности — число вычислений функции, так как зачастую именно оно доминирует в суммарных вычислениях. Градиенты дают много информации, но их вычисление зачастую сложно (градиент — минимум N+1 вычисление функции; аппроксимация Гессе ~N²). Например, метод Ньютона требует второго порядка производных; простые градиентные методы — только N (но обычно больше итераций). Лучший вариант зависит от конкретной задачи.

Методы:

• Использующие Гессе (или приблизительные Гессе через конечные разности):
  • Метод Ньютона.
  • Последовательное квадратичное программирование — метод Ньютона для малых/средних задач с ограничениями; отдельные версии для задач большой размерности.
  • Методы внутренней точки — широкий класс методов для ограниченных задач; отдельные варианты используют только градиенты/субградиенты, другие — Гессе.
• Градиентные методы и методы с аппроксимацией градиента (или субградиента):
  • Координатный спуск — поочерёдное обновление каждой переменной.
  • Метод сопряжённых градиентов — для больших задач; теоретически конечен для квадратичных функций, но не реализуется на практике на машинах с конечной точностью.
  • Градиентный спуск (или метод наискорейшего спуска) — исторический (медленный) метод, возрождается для гигантских задач.
  • Субградиентный метод — итерационный подход для крупномасштабных задач с липшицевыми функциями (по Борису Поляку схожи с методами сопряжённых градиентов).
  • Bundle-метод спуска — для малых и средних задач с не-гладкими функциями, прежде всего выпуклых.
  • Эллипсоидный метод — для малых задач с квазивыпуклой функцией, важен теоретически (доказательство полиномиальной сложности для ряда комбинаторных задач). Связан с квазиньютоновскими методами.
  • Условный градиент (Франка — Вульфа) — для задач специальной структуры с линейными ограничениями.
  • Квазиньютоновские методы — для средних и больших задач (например, N<1000).
  • Simultaneous perturbation stochastic approximation — стохастическая оптимизация, эффективное случайное приближение градиента.
• Только значения функции (градиенты аппроксимируются разностями):
  • Интерполяционные методы.
  • Методы поиска по образцу — с лучшей сходимостью, чем Нелдер — Мид.
  • Метод зеркального спуска.

Помимо явно сходящихся алгоритмов и итерационных методов, применяются эвристики — алгоритмы без гарантированной сходимости, но полезные в практике. Известные примеры:

При расчётах динамики твёрдых тел и, в частности, динамики сочленённых систем часто применяют математическое программирование: например, динамика тела как решение ОДУ на многообразии ограничений^[9]; ограничения — различные нелинейные геометрические условия («точки совпадают», «поверхности не пересекаются» и т. д.). Добавление контактных сил сводят к решению задач о линейной комплементарности, эквивалентных квадратичным задачам оптимизации.

Многие задачи проектирования, включая инженерную оптимизацию и многодисциплинарную оптимизацию, — это тоже задачи оптимизации. Особенно распространено в авиакосмической отрасли.

Методы оптимизации применяются и в космологии, астрофизике^[10].

Экономика тесно связана с оптимизацией: классическое определение предмета экономики — «наука о человеческом поведении как отношении между целями и ограниченными ресурсами» с альтернативными способами использования^[11]. Современная теория оптимизации включает методы экономического равновесия, входит в сферу игровой теории. В JEL кодах математическое программирование и оптимизационные методы — C61-C63.

В микроэкономике решение задач максимизации полезности и двойственных задач моделируется как оптимизация. Поведение потребителей трактуется как максимизация полезности, а фирм — прибыли; при этом часто модели закладывают отвращение к риску. Многие модели финансов построены на стохастических оптимизационных методах. Оптимизация портфеля — пример мульткритериальной задачи.

С 1970-х годов динамическое принятие решений моделируется с помощью оптимального управления^[12]. Например, модели поиска работы — предмет экономики труда^[13][14][15].

В электротехнике оптимизационные методы применяют для проектирования фильтров^[16], защиты от магнитных полей, space mapping — проектирования СВЧ-структур^[17], проектирования антенн^[18][19], моделирования электромагнитных устройств^[20][21]. Применяют и в анализе потоков мощности^[22].

В гражданском строительстве оптимизация востребована для управления строительством, транспортных задач (проектирование и содержание дорожных сетей, анализ жизненного цикла объектов^[23], распределение ресурсов, управление водными ресурсами, управление движением^[24], оптимального планирования строительства и др.

Исследование операций использует оптимизационные методы повсеместно^[25]. Помимо классических техник, активно применяются стохастическое программирование, моделирование и имитация, крупномасштабная оптимизация.

Оптимизация используется в проектировании современных систем управления. Высокоуровневые регуляторы типа предиктивное управление моделью или оптимизация в реальном времени решают задачи непосредственно в ходе работы процесса с учётом ограничений и моделей системы.

В геофизических задачах оптимизация применяется для оценки параметров среды по косвенным измерениям (например, сейсмическим данным): восстанавливаются физические свойства и структуры подповерхностных слоёв. Задачи обычно нелинейны; используются и детерминированные, и стохастические методы.

Для конформационного анализа молекул широко применяются нелинейные методы оптимизации.

Алгоритмы оптимизации используются в построении биологических моделей, планировании экспериментов, метаболической инженерии и синтетической биологии^[26]. Линейное программирование применяется для расчёта максимальных выходов продуктов^[26] для вывода генетических регуляторных сетей по данным микромассивов^[27], и анализа транскрипционных сетей^[28]. Нелинейное программирование — при анализе энергетического обмена^[29], в метаболической инженерии и параметрической идентификации^[30].