Центральная предельная теорема
Центра́льные преде́льные теоре́мы (ЦПТ) — это совокупность теорем в теории вероятностей, которые играют важную роль в математической статистике и вероятностной теории. ЦПТ формулируют общие закономерности поведения средних значений и сумм случайных величин, подчиняющихся определенным условиям[2].
ЦПТ имеют важное практическое применение в статистике и науке в целом. Они позволяют делать выводы о параметрах совокупности на основе представительной выборки, используя методы статистического вывода. Кроме того, они являются основой для многих статистических методов, включая доверительные интервалы и проверку гипотез[1].
ЦПТ имеют широкое применение в различных областях: от экономики и финансов до медицины и социологии, где столкновение с большими объемами данных является обычным. Они позволяют получить надежные результаты на основе ограниченной выборки, что экономит время и ресурсы и повышает качество научных исследований[2].
Таким образом, центральные предельные теоремы играют важную роль в статистике и науке в целом. Они позволяют делать выводы на основе выборки, строить статистические модели и принимать обоснованные решения в различных областях деятельности[1].
Классическая ЦПТ
Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию . Пусть также
- .
Тогда
- по распределению при ,
где — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Определяя выборочное среднее первых величин как
- ,
мы можем переписать результат центральной предельной теоремы в следующем виде:
- по распределению при .
Скорость сходимости можно оценить с помощью неравенства Берри — Эссеена.
Замечания
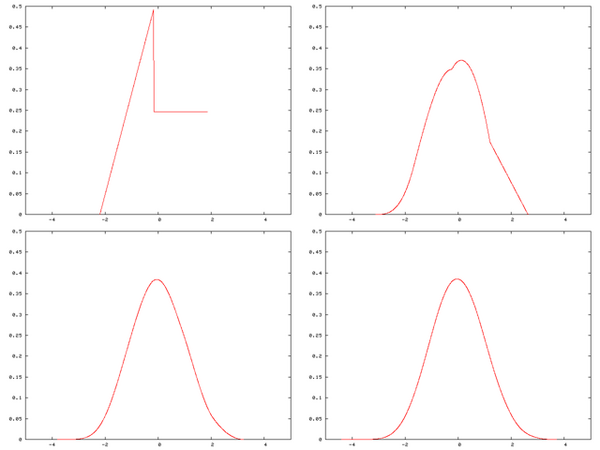
- Неформально говоря, классическая центральная предельная теорема утверждает, что сумма независимых одинаково распределённых случайных величин имеет распределение, близкое к . Эквивалентно, имеет распределение близкое к .
- Так как функция распределения стандартного нормального распределения непрерывна, сходимость к этому распределению эквивалентна поточечной сходимости функций распределения к функции распределения стандартного нормального распределения. Положив , получаем , где — функция распределения стандартного нормального распределения.
- Центральная предельная теорема в классической формулировке доказывается методом характеристических функций (теорема Леви о непрерывности).
- Вообще говоря, из сходимости функций распределения не вытекает сходимость плотностей. Тем не менее в данном классическом случае это имеет место.
Локальная ЦПТ
В предположениях классической формулировки, допустим в дополнение, что распределение случайных величин абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение также абсолютно непрерывно, и более того,
- при ,
где — плотность случайной величины , а в правой части стоит плотность стандартного нормального распределения.
Обобщения
Результат классической центральной предельной теоремы справедлив для ситуаций гораздо более общих, чем полная независимость и одинаковая распределённость.
[2]Пусть независимые случайные величины определены на одном и том же вероятностном пространстве и имеют конечные математические ожидания и дисперсии: .
Пусть .
Тогда .
И пусть выполняется условие Линдеберга:
Тогда
- по распределению при .
Пусть выполнены базовые предположения ЦПТ Линдеберга. Пусть случайные величины имеют конечный третий момент. Тогда определена последовательность
- .
Если предел
- (условие Ляпунова),
то
- по распределению при .
Пусть процесс является мартингалом с ограниченными приращениями. В частности, допустим, что
и приращения равномерно ограничены, то есть
Введём случайные процессы и следующим образом:
и
- .
Тогда
- по распределению при .
Пусть последовательность независимых и одинаково распределённых случайных векторов, каждый из которых имеет среднее и невырожденную матрицу ковариаций . Обозначим через вектор частичных сумм. Тогда при имеет место слабая сходимость распределений векторов
, где имеет распределение .



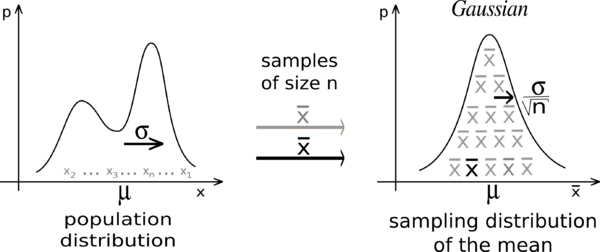




















![{\displaystyle \mathbb {E} [X_{i}]=\mu _{i},\;\mathrm {D} [X_{i}]=\sigma _{i}^{2}}](https://ru.ruwiki.ru/api/rest_v1/media/math/render/svg/e7f5a78381e7a567e4f7572d37a06d18436f45b5)
![{\displaystyle \mathbb {E} [S_{n}]=m_{n}=\sum \limits _{i=1}^{n}\mu _{i},\;\mathrm {D} [S_{n}]=s_{n}^{2}=\sum \limits _{i=1}^{n}\sigma _{i}^{2}}](https://ru.ruwiki.ru/api/rest_v1/media/math/render/svg/f5a237627ac173f9ac6c671f58962f13d8ca7018)
![{\displaystyle \forall \varepsilon >0,\;\lim \limits _{n\to \infty }\sum \limits _{i=1}^{n}\mathbb {E} \left[{\frac {(X_{i}-\mu _{i})^{2}}{s_{n}^{2}}}\,\mathbf {1} _{\{|X_{i}-\mu _{i}|>\varepsilon s_{n}\}}\right]=0,}](https://ru.ruwiki.ru/api/rest_v1/media/math/render/svg/981816483ed048fc438b79a56fe72a0e5e321bf0)



![{\displaystyle r_{n}^{3}=\sum _{i=1}^{n}\mathbb {E} \left[|X_{i}-\mu _{i}|^{3}\right]}](https://ru.ruwiki.ru/api/rest_v1/media/math/render/svg/3331df2595e9e85c82645024f4ad5c790c82a60e)


![{\displaystyle \mathbb {E} \left[X_{n+1}-X_{n}\mid X_{1},\ldots ,X_{n}\right]=0,\;n\in \mathbb {N} ,\;X_{0}\equiv 0,}](https://ru.ruwiki.ru/api/rest_v1/media/math/render/svg/8fab111d7a15486f76b27b8027dfe5888bc9d6a6)



![{\displaystyle \sigma _{n}^{2}=\mathbb {E} \left[(X_{n+1}-X_{n})^{2}\mid X_{1},\ldots ,X_{n}\right]}](https://ru.ruwiki.ru/api/rest_v1/media/math/render/svg/4452cea72a60fdae091fc5cec0fcc7d532cbc362)








