Конический маятник

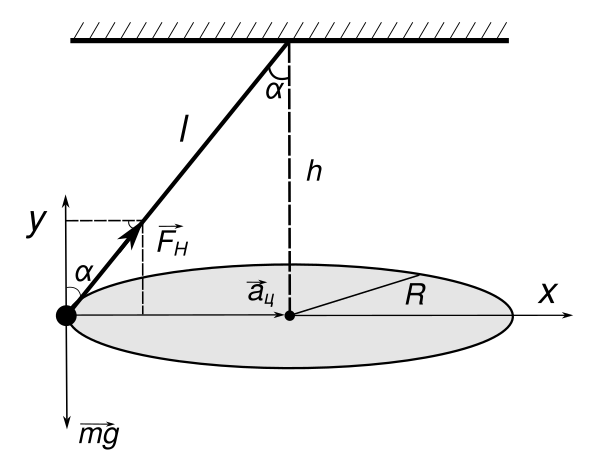
Конический маятник — частный случай физического маятника. Конический маятник представляет собой тонкую нерастяжимую нить длиной ${\displaystyle l}$, на конце которой закреплён груз (обычно тело в виде шара) массой ${\displaystyle m}$. Особенностью его является то, что, в отличие от математического маятника, совершающего колебания в одной плоскости ${\displaystyle xy}$, тело конического маятника совершает вращение в горизонтальной плоскости по окружности радиуса ${\displaystyle R}$. Горизонтальная плоскость отстоит от точки подвеса на расстоянии ${\displaystyle h}$. Нить конического маятника отклонена от вертикали на угол ${\displaystyle \alpha }$, величина которого не изменяется при колебаниях конического маятника. Нить маятника описывает в пространстве коническую поверхность. На тело маятника действуют сила тяжести ${\displaystyle {\vec {mg}}}$ и сила натяжения нити ${\displaystyle {\vec {F_{H}}}}$ (см. рисунок).

Уравнение движения конического маятника имеет вид:

${\displaystyle {\vec {mg}}+{\vec {F_{H}}}={\vec {ma_{c}}}}$.

Проекции на оси ${\displaystyle ox}$, ${\displaystyle oy}$, соответственно, равны:

${\displaystyle ox:F_{H}\sin \alpha =ma=m\omega ^{2}R=m{\Biggl (}{\frac {2\pi }{T}}{\Biggl )}^{2}R}$,

${\displaystyle oy:F_{H}\cos \alpha -mg=0}$.

Центростремительное ускорение ${\displaystyle a_{c}}$ равно:

${\displaystyle a_{c}=g{\frac {R}{h}}=\omega ^{2}R={\Biggl (}{\frac {2\pi }{T}}{\Biggl )}^{2}R}$,

откуда период колебаний конического маятника:

${\displaystyle T=2\pi {\sqrt {\frac {h}{g}}}}$.

Если угол отклонения конического маятника невелик, т. е. ${\displaystyle h\thicksim l}$, формула периода конического маятника принимает вид:

${\displaystyle T\thickapprox 2\pi {\sqrt {\frac {l}{g}}}}$.

Первоначально конические маятники использовались в механических часах. Их преимуществом перед обычными маятниками было движение без рывков (обычным маятником свойственна точка остановки в моменты максимального отклонения). Нашли применение коническим маятникам и в механизмах навигационных маяков (поворотные механизмы отражающей линзы, часто линзы Френеля), и в телескопах, где существенным фактором является плавность движения оптического устройства вокруг своей оси, что позволяло, например, синхронизировать движение Земли и телескопа, обеспечивая неподвижность точки наблюдения. Известно применение конического маятника в машине Дж. Уатта (центробежный регулятор скорости паровых двигателей). Некоторые аттракционы в парках для развлечений являются, по сути, коническими маятниками.