Амплитуда
В физике амплитуда (от лат. amplitūdō) — это характеристика осцилляционного движения, волнового процесса или электромагнитного сигнала, определяющая максимальное отклонение смещения или другой величины, изменяющейся периодически или квазипериодически во времени[1]. Это расстояние между наиболее удалённой точкой волны и точкой равновесия или положением середины.
Определения
Для симметричных периодических волн, таких как синусоидальная волна, прямоугольная волна или треугольная волна, термины «амплитуда пика» и «полуамплитуда» эквивалентны.
В измерениях в области аудиосистем, телекоммуникаций и других областях, где измеряемая величина — это сигнал, колеблющийся выше и ниже некоторого опорного значения, но не обязательно являющийся синусоидой, часто используют амплитуду пика. Если опорное значение — ноль, то речь идёт о максимальном по модулю значении сигнала; если опорным значением является среднее значение (постоянная составляющая), амплитуда пика — это максимальное (по модулю) отклонение относительно этого опорного значения.
Полуамплитуда — это половина амплитуды «пик-пик»[2]. В большинстве научной литературы[3] термин «амплитуда» или «амплитуда пика» часто обозначает полуамплитуду.
Это наиболее используемый параметр при анализе орбитальных колебаний в астрономии, и измерение малых значений радиальной полуамплитуды у ближайших звёзд актуально для поиска экзопланет[4].
Обычно использование «амплитуды пика» однозначно только для симметричных периодических волн (синусоида, прямоугольная или треугольная волна). В случае асимметричных волн (например, периодически повторяющихся односторонних импульсов) понятие амплитуды пика становится неоднозначным. Значение будет различаться в зависимости от того, определяется ли максимальная положительная величина относительно среднего значения, максимальная отрицательная — относительно среднего, или же разница между пиковым положительным и отрицательным значениями (амплитуда «пик-пик»), делённая на два (полуамплитуда). В электротехнике для устранения этой неоднозначности амплитуду обычно измеряют относительно определённого потенциала (например, земли или 0 В). В этом случае речь идёт не столько об амплитуде, сколько о максимальном отклонении относительно произвольного уровня (постоянной составляющей).
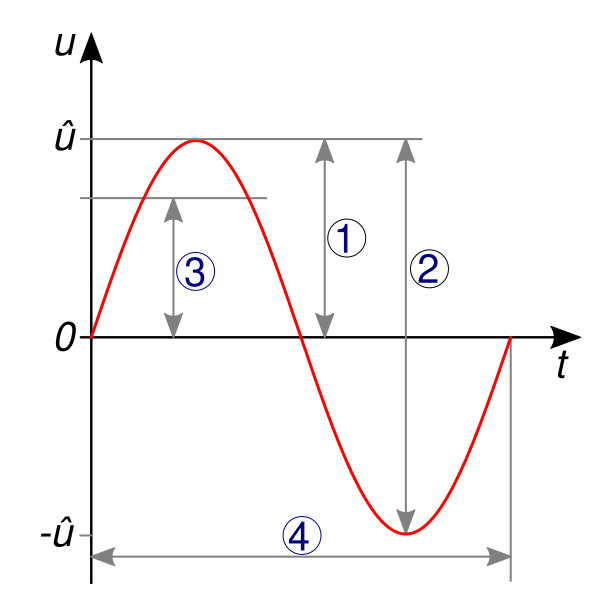
Амплитуда «пик-пик» (сокращённо p-p) — это разность между максимальным (положительным) и минимальным (отрицательным) значениями амплитуды. В соответствующих схемах её можно измерить с помощью приборов или по изображению формы сигнала на осциллографе. На экране осциллографа пики формы сигнала легко распознаются и измеряются по разметке. Такой способ измерения остаётся распространённым, однако в ряде случаев уместнее использовать другие параметры амплитуды.
Среднеквадратическая амплитуда (RMS, от англ. root mean square) широко применяется в электротехнике; она определяется как квадратный корень из среднего по времени квадрата вертикального отклонения графика от состояния покоя[5]; то есть это эффективное значение переменного сигнала (без постоянной составляющей).
Для сложных или нерегулярных форм сигнала (например, шума) часто предпочтительнее применять именно среднеквадратическую амплитуду, так как она уникальна и физически осмысленна. Например, средняя мощность, переносимая акустической, электромагнитной или электрической волной, пропорциональна квадрату среднеквадратической амплитуды (а не, вообще говоря, квадрату амплитуды пика)[6].
В системах переменного тока принято (стандарт во всём мире) указывать именно эффективные (среднеквадратичные) значения синусоидальных напряжений и токов. Особенность RMS-напряжений и токов — в том, что они создают такое же тепловое действие, как и соответствующий постоянный ток на данном резисторе.
Значение «пик-пик» используют, например, при выборе выпрямителей для источников питания или при оценке величины напряжения, максимальную амплитуду которого должен выдерживать изоляционный материал. Многие распространённые вольтметры откалиброваны на RMS-значение, но измеряют среднее значение выпрямленного сигнала. Цифровые вольтметры и все магнитоэлектрические приборы относятся к этой категории. Такая RMS-калибровка корректна только для синусоидальных сигналов, поскольку соотношения между пиковым, средним и RMS-значениями зависят от формы волны. Для сигналов, существенно отличающихся от синусоиды, соотношение между RMS и средним значением изменяется. Истинные RMS-приборы применялись в радиочастотных измерениях, где влияние определялось нагреванием резистора. Появление микропроцессорных приборов для расчёта истинного RMS путём дискретизации формы волны сделало такие измерения стандартом.
В телекоммуникациях термин «амплитуда импульса» означает значение параметра импульса, такого как напряжение, ток, напряжённость поля или мощность.
Амплитуда импульса измеряется относительно заданного уровня, поэтому её сопровождают уточняющими определениями, такими как «среднее», «мгновенное», «пиковое» или «среднеквадратичное».
Также понятие амплитуды импульса используют по отношению к огибающей амплитуды при частотной или фазовой модуляции формы сигнала[7].
Формальное представление
В простейшем случае волновое уравнение записывается как
где:
- — амплитуда (или амплитуда пика),
- — осциллирующая переменная,
- — угловая частота,
- — время,
- и — произвольные постоянные, определяющие фазовый и координатный сдвиги соответственно.
Размерность амплитуды зависит от измеряемой величины:
- для колеблющейся струны — это расстояние;
- для звуковой волны амплитуда соответствует акустическому давлению. Единица измерения — паскаль (Па).
Примечание: измерения часто приводят к выражению уровня акустического давления в децибелах (дБ) относительно эталонной величины 20 мкПа (0 дБ), причём нулевая амплитуда соответствует −∞ дБ. Это значение не связано напрямую с амплитудой, а зависит от формы сигнала (см. кре́ст-фактор). - для электромагнитного излучения — это величина электрического поля;
- для электрического сигнала — это напряжение либо ток.
Амплитуда в приведённом выше понимании не вполне подходит для задач анализа передачи мощности. Например, в акустике и электротехнике используют эффективное значение — среднеквадратичную величину сигнала.
В случае переменной сигнальной формы анализируют также максимальные значения за определённый период: «амплитуда пика» либо «максимальная амплитуда».
| Название | Определение |
|---|---|
| Средняя амплитуда | Среднее арифметическое положительных значений сигнала |
| RMS-амплитуда | Приведённое к постоянной, эффективное значение мощности, также известное как эффективное значение. |
| Амплитуда | Максимальное положительное значение, также известно как максимальное значение. |
| Амплитуда «пик-пик» | Разница между максимальным (положительным) и минимальным (отрицательным) значениями сигнала. |
Амплитуда волны
Волна — это физическое возмущение, распространяющееся в пространстве, например, гармоническая волна. Математически такую волну можно описать функцией , зависящей от времени и координат в пространстве:
Здесь — скорость распространения возмущения. Для плоской волны, распространяющейся по оси x, решение имеет вид:
В этом случае амплитуда определяется как:
Часто интенсивность волны пропорциональна среднему значению квадрата амплитуды:
Для периодической волны с периодом T:
Амплитуда в акустике
В акустике амплитуду обычно измеряют в децибелах SPL ():
- Децибелы характеризуют отношение двух величин и определяются как десятичный логарифм их отношения.
- Аббревиатура SPL (Sound Pressure Level) означает уровень звукового давления.
Если акустическая волна создаёт максимальное избыточное давление в некоторой точке пространства, то амплитуда в децибелах SPL выражается как:
где — опорный уровень звукового давления.
Волны по мере распространения «ослабевают в амплитуде», то есть амплитуда уменьшается с удалением от источника — это называется затухание волны. При этом длина волны и частота волны не изменяются, так как зависят только от характеристик источника.
Падение амплитуды звуковой волны имеет две главные причины:
- Увеличение фронта волны, что приводит к уменьшению амплитуды в соответствии с законом обратных квадратов.
- Поглощение вибраций — диссипативный процесс, при котором часть звуковой энергии уходит в материал, являющийся акустическим изолятором.
Единицы измерения амплитуды
Единицы амплитуды зависят от природы колебательного явления:
- Для переменного тока обычно используют среднеквадратичное значение амплитуды, измеряемое в вольтах или амперах, в зависимости от рассматриваемой величины[8].[9]
- Для электромагнитной волны амплитуда соотносится с квадратным корнем из радиантной интенсивности и определяется величиной электрического поля. Для световой волны важна также световая интенсивность, обычно измеряемая в канделах.
- Для звуковой волны амплитуда определяется избыточным давлением (единицы — паскаль, миллибар и др.)[8][9]
- Для механических волн или вибраций амплитуда — это смещение, выражаемое в единицах длины.
- Для электромагнитного излучения амплитуда отдельного фотона отражает изменения электрического поля волны. При передаче радиосигнала интенсивность или частота такого излучения может модулироваться соответствующим образом (амплитудная модуляция, частотная модуляция).
Полуамплитуда
Полуамплитуда — это половина значения амплитуды «пик-пик»[2]. Это наиболее распространённая характеристика при анализе орбитальных амплитуд в астрономии, и измерение малых полуамплитуд у близких звёзд важно для поиска экзопланет[10]. Для синусоидальной волны амплитуда пика и полуамплитуда совпадают.
Некоторые специалисты[11] используют термины «амплитуда» или «амплитуда пика» для обозначения полуамплитуды (половины амплитуды «пик-пик»), что указывается, в частности, в ряде публикаций[2].
Огибающие переходных амплитуд
Амплитуда в установившемся состоянии во времени не меняется, её можно задать скалярно. В противном случае амплитуда — переходное (временное) явление и должна описываться как непрерывная функция или дискретный вектор. Для аудиосигналов переходные огибающие амплитуды лучше отражают структуру, поскольку многие звуки состоят из фаз атаки, затухания, устойчивой части и релиза.
Огибающие переходных амплитуд или огибающие устойчивых состояний могут быть заданы и для других параметров: модуляции по частоте/амплитуде, гауссовского шума, обертонов и проч.[12]
Нормализация амплитуды
Для сигналов, содержащих множество обертонов, комплексные переходные тембры можно получить, задавая каждой гармонике свою собственную огибающую переходной амплитуды. Это может приводить к дополнительной модуляции громкости. Для независимого контроля над громкостью и тембром огибающие гармоник нормализуют покадрово — то есть каждое мгновение их сумма равна 100 % (или 1). Основная огибающая, управляющая громкостью, остаётся независимой[12].
В задачах распознавания звука максимальная нормализация амплитуды помогает соотнести ключевые гармонические характеристики двух звуков, что позволяет выявлять схожие тембры независимо от их громкости[13].
Примечания
Литература
- Ilja N. Bronstein, Konstantin A. Semendjaev, Gerhard Musiol, Heiner Mühlig. Taschenbuch der Mathematik. 5-е издание. Harri Deutsch, Thun et al., 2001. ISBN 3-8171-2005-2.
- Christian Gerthsen. Physik. Springer-Verlag.



![{\displaystyle x=A\sin(\omega [t-K])+b,}](https://ru.ruwiki.ru/api/rest_v1/media/math/render/svg/658e087c8d361b4d8322e09f8df1d2cc7f0feb29)
















