Регрессионный анализ
Регрессионный анализ (англ. regression analysis) — совокупность статистических методов для оценки зависимости между одной зависимой переменной (также называемой результативной, откликом или, в терминах машинного обучения, меткой) и одной или несколькими независимыми переменными (регрессорами, предикторами, ковариатами, объясняющими переменными или признаками)[1][2].
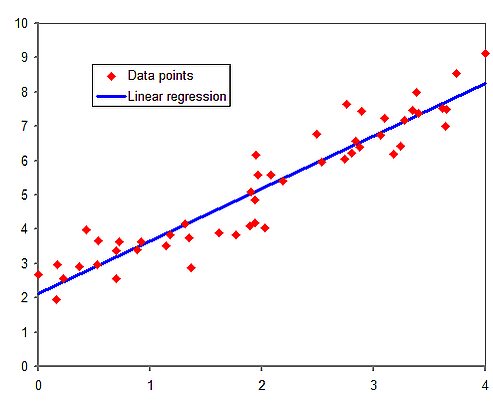
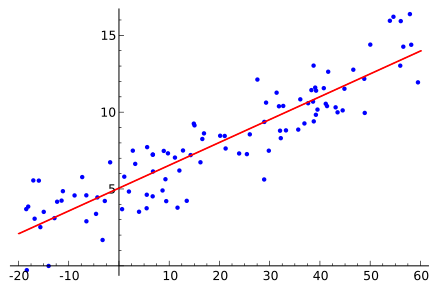
Наиболее распространённой формой регрессионного анализа является линейная регрессия, в которой определяется линия (или более сложная линейная комбинация), наилучшим образом соответствующая данным согласно некоторому математическому критерию. Например, метод наименьших квадратов находит единственную прямую (или гиперплоскость), минимизирующую сумму квадратов отклонений между истинными данными и этой линией (или гиперплоскостью). Такой подход позволяет оценить условное математическое ожидание (или среднее значение по совокупности) зависимой переменной при заданных значениях независимых. Существуют и другие методы регрессии — например, квантильная регрессия или анализ необходимых условий[3] — для оценки альтернативных характеристик, а также непараметрическая регрессия для работы с более широким классом нелинейных моделей.
Регрессионный анализ применяется, главным образом, для двух разных задач: во-первых, для прогнозирования и экстраполяции, где его область существенно пересекается с машинным обучением; во-вторых, для выявления причинно-следственных связей между независимыми и зависимой переменными. Следует помнить, что результаты регрессии сами по себе показывают лишь наличие статистической связи между переменными в фиксированных данных; обоснование предсказательной или причинной силы требует отдельного анализа. Особенно это актуально при работе с обсервационными данными[4][5].
История
Наиболее ранние зачатки регрессионного анализа можно найти в трудах Исаака Ньютона около 1700 года при изучении равноденствий. Ему приписывают введение «эмбрионального анализа линейной регрессии»: не только используя усреднение данных за 50 лет до Тобиаса Майера, но и подводя сумму остатков к нулю, он вынуждал прямую регрессии проходить через среднюю точку. Ещё раньше, в работе 1671 года о кольцах Ньютона, он применял усреднение, что было новшеством для того времени[6][7].
Метод наименьших квадратов был опубликован Лежандром в 1805 году[8] и независимо Гауссом в 1809[9]. Оба ученых применяли этот метод для вычисления орбит небесных тел по астрономическим наблюдениям. В 1821 году Гаусс опубликовал дальнейшее развитие теории наименьших квадратов[10], включая версию теоремы Гаусса — Маркова.
Термин «регрессия» был введён Фрэнсисом Гальтоном в XIX веке для описания биологического явления — возврата роста потомков высоких предков к среднему значению (известно как регрессия к среднему)[11][12]. Сначала термин «регрессия» имел только биологический смысл[13][14], однако работы Юдни Юля и Карла Пирсона расширили идею на статистический анализ[15][16], предполагая нормальное распределение совместного распределения отклика и объясняющих переменных. Это ограничение было ослаблено Р. А. Фишером в работах 1922 и 1925 годов[17][18][19], который предположил лишь условное распределение отклика по нормальному закону.
В 1950–1960-х годах экономисты для проведения регрессии пользовались электромеханическими калькуляторами, и вычисление одного анализа могло занимать до суток[20].
Методы регрессии остаются предметом активных исследований: разработаны робастные методы регрессии, работающие с коррелированными откликами, временными рядами, кривыми роста, с изображениями, графами или другими сложными объектами, а также техники для неполных данных, байесовские методы регрессии, регрессия при ошибках измерения, с количеством признаков большим числа наблюдений и для вывода причинности. Современный анализ осуществляется с помощью статистических и табличных программ на компьютерах и калькуляторах.
Регрессионная модель
На практике исследователь вначале выбирает модель для оценки, а затем с помощью выбранного метода (например, метод наименьших квадратов) определяет параметры. Регрессионные модели содержат следующие компоненты:
- Неизвестные параметры — скаляр (или вектор) .
- Независимые переменные — наблюдаемые данные, часто вектор .
- Зависимая переменная — наблюдаемая, часто скаляр .
- Ошибки модели — не наблюдаются напрямую, обычно .
В разных сферах терминология для зависимых и независимых переменных может отличаться.
Обычно предполагается, что — некоторая функция (регрессионная функция) от и плюс случайная ошибка :
В стандартной модели независимые переменные считаются безошибочными. Если содержат ошибку, используется модель с ошибками в переменных. Варианты моделей существуют и для случаев пропущенных или смешивающих переменных, эндогенности и прочего.
Цель анализа — аппроксимировать функцию , максимально близкую к наблюдаемым данным. Обычно форма функции выбирается исходя из предметной области или удобных допущений: например, простая регрессия предполагает модель .
После выбора статистической модели параметры оцениваются разными методами. Метод наименьших квадратов минимизирует сумму квадратов ошибок и выдаёт оценку . Эта оценка позволяет получить прогноз или анализировать объяснённую моделью вариацию. В линейной регрессии найденная функция приближает условное математическое ожидание [9]. Альтернативные методы (например, квантильная регрессия) могут использовать другие критерии.
Для оценки регрессионной модели данных должны быть достаточно: при строках и параметрах необходимо независимых наблюдений. Если , существует бесконечно много решений, а если , — их нет, которые бы идеально подошли под данные. Задачу можно записать в виде системы уравнений; число называется степенями свободы модели. Также независимые переменные должны быть линейно независимы, чтобы существовало единственное решение .
Основные предположения
Чтобы трактовать регрессию как статистическую модель, часто используются классические статистические предположения:
- Выборка репрезентативна для всей совокупности.
- Независимые переменные измерены без ошибки.
- Ожидаемое значение ошибки при заданных значениях объясняющих переменных равно нулю: .
- Дисперсия ошибок идентична во всех наблюдениях.
- Ошибки не коррелированы между собой (ковариационная матрица диагональна).
При некоторых условиях оценки методом наименьших квадратов являются несмещёнными, состоятельными и эффективными (теорема Гаусса — Маркова). Для учета нарушений классических предположений разработаны подходы: моделирование ошибок в переменных; устойчивые к гетероскедастичности стандартные ошибки; коррелированные ошибки — с помощью кластерных или стандартных ошибок Ньюи — Уэста. В геостатистике способ задания ошибок по пространственным единицам существенно влияет на результаты анализа[21][22]. В эконометрике существует множество методов исправления нарушений предположений на практике.
Линейная регрессия
В линейной регрессии спецификация модели заключается в том, что зависимая переменная выражается линейной комбинацией параметров (но не обязательно линейной по независимым переменным). Например, для простой линейной регрессии:
В случае нескольких независимых переменных (или их функций) используется множественная регрессия. Рассмотрим добавление квадратичного члена:
Это всё ещё линейная регрессия относительно параметров .
В обоих случаях — ошибка, — наблюдение.
Если взять случайную выборку, то оценки параметров дают модель:
Остаток — разница между прогнозируемым и истинным значением. Классический способ оценивания — метод наименьших квадратов, минимизирующий сумму квадратов остатков (SSR):
Минимизация SSR приводит к нормальным уравнениям, из которых можно выражать параметры .
Для простой линейной регрессии оценки:
где и — средние значения соответственно и .
Если вариация ошибок постоянна, её оценка:
Это среднеквадратичная ошибка модели. Размер знаменателя зависит от числа параметров: для одного признака [23].
Стандартные ошибки для оценок:
Если ошибки распределены нормально, по этим оценкам строятся доверительные интервалы и проводятся тесты о параметрах.
В более общей множественной регрессии с независимыми переменными:
Если для всех , — свободный член (перехват).
Параметры находятся решением нормальных уравнений; остаток:
В матричной форме:
Решение:
После построения модели важно проверить качество аппроксимации и значимость оценённых параметров: это R-квадрат, анализ распределения остатков, тесты гипотез. Обычно используется F-критерий для всей модели и t-критерий для отдельных параметров.
Интерпретация результатов диагностик зависит от предположений модели. При больших отклонениях, например, если ошибки не нормальны, анализ усложняется. При больших выборках применим центральная предельная теорема.
Ограниченные зависимые переменные (категориальные или с ограниченным диапазоном) часто встречаются в эконометрике. Если зависимая переменная бинарна, а анализ проводится с помощью линейной регрессии, говорят о линейной вероятностной модели. Нелинейные аналоги — пробит-модель, логит-модель, для многомерного случая — многомерная пробит-модель. Для нескольких категорий используются мультиномиальная логит-модель, для порядковых — упорядоченная логит-модель, упорядоченная пробит-модель. Цензурированная регрессия применяется, если зависимая регистрируется только иногда, а корректировка Хекмана — при нерепрезентативной выборке.
Альтернатива — линейная регрессия на полихорических и полисерийных коэффициентах. В случае положительных счетных данных — пуассоновская регрессия, негативно-биномиальная модель.
Нелинейная регрессия
Нелинейная регрессия применяется, если модель не линейна по параметрам. Минимизация суммы квадратов требует итерационных вычислений, что приводит к целому ряду дополнительных сложностей.
Прогнозирование (интерполяция и экстраполяция)
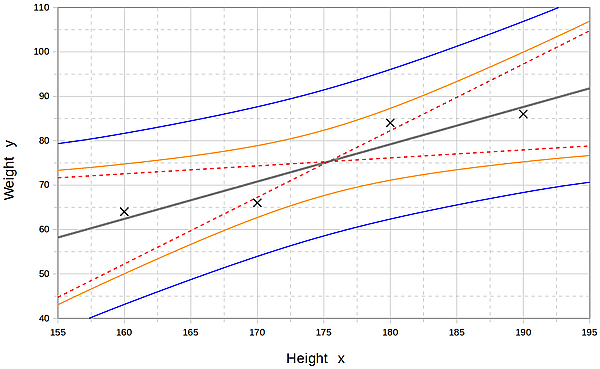
Регрессионные модели позволяют предсказывать значения переменной при известных значениях . Предсказание внутри диапазона исходных данных называют интерполяцией, вне — экстраполяцией. Экстраполяция требует строгого соблюдения предположений модели: чем дальше прогноз выходит за пределы исходных данных, тем менее надежным он становится.
К точечному прогнозу часто добавляют интервал прогнозирования, который быстро расширяется при выходе за пределы исходных данных.
Поэтому многие исследователи не рекомендуют строить экстраполяции[25].
Совпадение формы регрессионной зависимости с реальностью — ещё один источник неопределённости. Даже при хорошем аппроксимировании имеющихся данных экстраполяция сильно зависит от предположенной структуры. Если известно, что зависимая переменная, например, не может принимать значения выше определённого предела, это учитывают при выборе формы модели. Такой подход позволяет сделать экстраполяцию «реалистичной».
Анализ мощности и размера выборки
Нет универсальных правил для числа наблюдений относительно количества независимых переменных модели. Одна из простых эвристик — , где — объём выборки, — количество независимых, — необходимое число наблюдений для одной переменной[26]. Например, чтобы построить линейную регрессию на 1000 пациентов и с 5 наблюдениями на переменную, максимальное число независимых приближённо равно 4, так как
- .
Другие методы
Помимо метода наименьших квадратов, параметры моделей могут оцениваться и другими способами:
- Байесовские методы — например, байесовская линейная регрессия.
- Проценты ошибок (процентная регрессия) — применяется, когда критична минимизация процентных, а не абсолютных ошибок[27].
- Метод наименьших модулей — надёжен при выбросах, приводит к квантильной регрессии.
- Непараметрическая регрессия — требует большого количества наблюдений; ресурсоёмка.
- Сценарная оптимизация — приводит к моделям, выдающим интервальные прогнозы.
Программное обеспечение
Все основные статистические пакеты выполняют регрессионный анализ и статистические тесты на его основе. Простая линейная регрессия и множественная оценка по методу наименьших квадратов доступна даже в табличных процессорах и калькуляторах. Для нелинейных и робастных методов широкой унификации нет: разное ПО реализует разные алгоритмы, иногда отличающиеся даже при одном названии. Существуют специализированные программы для регрессии в областях обследований и нейровизуализации.
Примечания
Литература
- William H. Kruskal, Judith M. Tanur (ред.) (1978), "Linear Hypotheses," International Encyclopedia of Statistics. Free Press, т. 1,
- Evan J. Williams, "I. Regression," c. 523–41.
- Julian C. Stanley, "II. Analysis of Variance," c. 541–554.
- D.V. Lindley (1987). "Regression and correlation analysis", New Palgrave: A Dictionary of Economics, т. 4, c. 120–23.
- Birkes, David; Yadolah Dodge. Alternative Methods of Regression. ISBN 0-471-56881-3
- Chatfield, C. (1993) "Calculating Interval Forecasts," Journal of Business and Economic Statistics, 11: 121–135.
- Draper, N.R. Applied Regression Analysis : [англ.] / N.R. Draper, H. Smith. — 3-е. — John Wiley, 1998. — ISBN 978-0-471-17082-2.
- Fox, J. (1997). Applied Regression Analysis, Linear Models and Related Methods. Sage
- Hardle, W. Applied Nonparametric Regression (1990), ISBN 0-521-42950-1
- Meade, Nigel; Islam, Towhidul (1995). “Prediction intervals for growth curve forecasts”. Journal of Forecasting [англ.]. 14 (5): 413—430. DOI:10.1002/for.3980140502. Дата обращения 2024-06-20.
|access-date=требует|url=(справка) - A. Sen, M. Srivastava. Regression Analysis — Theory, Methods, and Applications. Springer-Verlag, Berlin, 2011 (4-е издание).
- T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). Vieweg+Teubner, ISBN 978-3-8348-1022-9.
- Stulp, Freek; Olivier Sigaud. Many Regression Algorithms, One Unified Model: A Review. Neural Networks, том 69, сентябрь 2015, c. 60–79. https://doi.org/10.1016/j.neunet.2015.05.005.
- Malakooti, B. (2013). "Operations and Production Systems with Multiple Objectives". John Wiley & Sons.
- Chicco, Davide; Warrens, Matthijs J.; Jurman, Giuseppe (2021). “The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation”. PeerJ Computer Science [англ.]. 7 (e623): e623. DOI:10.7717/peerj-cs.623. PMC 8279135. PMID 34307865.
|access-date=требует|url=(справка)
Ссылки
- Earliest Uses: Regression — происхождение термина и справочная информация (англ.)
- Что такое множественная регрессия? (англ.)
- Регрессия слабо коррелированных данных — как ошибки линейной регрессии возникают при меньшем разбросе Y (англ.)