Параметр

Когда система моделируется с помощью уравнений, значения, описывающие систему, называются параметрами. В механике массы, размеры и формы (для твёрдых тел), плотности и вязкости (для жидкостей) выступают в качестве параметров в уравнениях, моделирующих движение. Часто существует несколько вариантов выбора параметров, и подбор удобного набора параметров называется параметризацией.

Если рассматривать движение объекта по поверхности сферы, значительно большей по размеру, чем сам объект (например, Земля), обычно используют две параметризации его положения: угловые координаты (широта/долгота), которые хорошо описывают большие перемещения по окружностям сферы; и направление и расстояние от известной точки (например, «10 км северо-западнее Торонто» или эквивалентно «8 км на север и затем 6 км на запад от Торонто»), что часто проще для перемещений в пределах относительно небольшой области, например, внутри страны или региона. Такие параметризации также важны для моделирования географических областей (например, при построении карт).

Математические функции имеют один или несколько аргументов, связанных с определением переменных. В определении функции также могут присутствовать параметры, но, в отличие от переменных, параметры не перечисляются среди аргументов функции. Если параметры присутствуют, определение фактически задаёт целое семейство функций — по одной для каждого допустимого набора значений параметров. Например, можно определить общую квадратичную функцию так:

${\displaystyle f(x)=ax^{2}+bx+c}$ ;

Здесь переменная x — аргумент функции, а a, b и c — параметры, определяющие, какую именно квадратичную функцию рассматривают. Параметр можно включить в обозначение функции, чтобы подчеркнуть зависимость от него. Например, логарифм по основанию b определяется формулой

${\displaystyle \log _{b}(x)={\frac {\log(x)}{\log(b)}}}$

где b — параметр, указывающий, какой логарифмической функцией пользуются. Это не аргумент функции, и, например, при рассмотрении производной ${\displaystyle \log _{b}'(x)=(x\ln(b))^{-1}}$ b считается постоянным.

В некоторых неформальных ситуациях вопрос о том, какие символы в определении функции считать параметрами, решается по соглашению или исторически. Однако изменение статуса символа между параметром и переменной меняет и саму функцию как математический объект. Например, обозначение падающего факториала

${\displaystyle n^{\underline {k}}=n(n-1)(n-2)\cdots (n-k+1)}$ ,

определяет полиномиальную функцию от n (если k — параметр), но не является полиномиальной функцией от k (если n — параметр). Более того, во втором случае функция определена только для неотрицательных целых аргументов. Более строгие формулировки подобных ситуаций обычно начинаются с функции многих переменных (включая все, что иногда называют «параметрами»):

${\displaystyle (n,k)\mapsto n^{\underline {k}}}$

как с основного объекта, а затем определяют функции с меньшим числом переменных посредством каррирования.

Иногда все функции с определёнными параметрами могут рассматриваться как параметрическое семейство, то есть как индексированное семейство функций.

В контексте математической модели, например распределения вероятностей, Бард описывает различие между переменными и параметрами следующим образом:

Мы называем отношения, которые, как предполагается, описывают определённую физическую ситуацию, моделью. Обычно модель состоит из одного или нескольких уравнений. Величины, встречающиеся в уравнениях, мы делим на переменные и параметры. Различие между ними не всегда очевидно и часто зависит от контекста, в котором появляются переменные. Обычно модель предназначена для объяснения связей между величинами, которые можно независимо измерить в эксперименте (переменные модели). Однако для формулировки этих связей часто вводятся «константы», отражающие присущие природе свойства (или свойства материалов и оборудования, используемых в данном эксперименте). Это и есть параметры^[4].

В аналитической геометрии кривые часто задаются как образ функции. Аргумент функции неизменно называют «параметром». Окружность радиуса 1 с центром в начале координат можно задать несколькими способами:

• Неявная форма: кривая включает все (x, y), удовлетворяющие уравнению

${\displaystyle x^{2}+y^{2}=1}$

• Параметрическая форма: кривая включает все точки (cos(t), sin(t)), когда t пробегает некоторое множество значений, например [0, 2π) или (−∞, ∞):

${\displaystyle (x,y)=(\cos t,\sin t)}$

где t — параметр.

Таким образом, эти уравнения, которые в других областях могли бы называться функциями, в аналитической геометрии характеризуются как параметрические уравнения, а независимые переменные считаются параметрами.

В математическом анализе часто рассматривают интегралы, зависящие от параметра. Они имеют вид

${\displaystyle F(t)=\int _{x_{0}(t)}^{x_{1}(t)}f(x;t)\,dx.}$

В этой формуле t одновременно является аргументом функции F и параметром в правой части, от которого зависит интеграл. При вычислении интеграла t считается постоянным, поэтому его называют параметром. Если требуется узнать значение F при разных t, то t становится переменной. Величина x — это фиктивная переменная или переменная интегрирования (иногда её также называют параметром интегрирования).

В статистике и эконометрике вероятностная основа сохраняется, но акцент смещается на оценивание параметров распределения по наблюдаемым данным или на проверку гипотез о них. В частотной статистике параметры считаются «фиксированными, но неизвестными», тогда как в байесовском подходе они трактуются как случайные величины, а их неопределённость описывается распределением.

В теории статистического оценивания термины «статистика» или оценка относятся к выборке, а «параметр» или оцениваемое значение — к генеральной совокупности, из которой взята выборка. Статистика — это числовая характеристика выборки, которую можно использовать как оценку соответствующего параметра — числовой характеристики генеральной совокупности.

Например, среднее выборки (оценка), обозначаемое ${\displaystyle {\overline {X}}}$, может использоваться как оценка параметра математического ожидания (оцениваемого значения), обозначаемого μ, генеральной совокупности, из которой взята выборка. Аналогично, выборочная дисперсия (оценка), обозначаемая S², может использоваться для оценки параметра дисперсии (оцениваемого значения), обозначаемого σ², генеральной совокупности (выборочное стандартное отклонение (S) не является несмещённой оценкой стандартного отклонения генеральной совокупности (σ)).

Можно проводить статистические выводы, не предполагая конкретного параметрического семейства распределений вероятностей. В этом случае говорят о непараметрической статистике в противоположность параметрической^[5]. Например, критерий, основанный на коэффициенте ранговой корреляции Спирмена, называют непараметрическим, поскольку статистика вычисляется по ранговому порядку данных, а не по их значениям (и, следовательно, независимо от распределения, из которого они взяты), тогда как критерии, основанные на коэффициенте корреляции Пирсона, являются параметрическими, так как вычисляются непосредственно по значениям данных и, следовательно, оценивают параметр, известный как корреляция генеральной совокупности^[6].

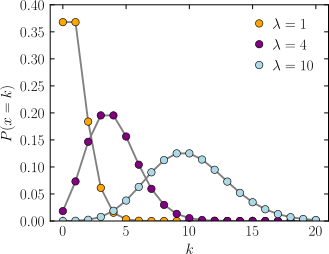
В теории вероятностей распределение случайной величины можно описать как принадлежащее к семейству распределений вероятностей, различающихся между собой значениями конечного числа параметров. Например, говорят о «распределении Пуассона со средним λ». Функция, определяющая распределение (так называемая функция вероятности), имеет вид:

${\displaystyle f(k;\lambda )={\frac {e^{-\lambda }\lambda ^{k}}{k!}}.}$

Этот пример иллюстрирует различие между константами, параметрами и переменными. Здесь e — число Эйлера, фундаментальная математическая константа. Параметр λ — среднее число наблюдаемых событий, характеристика системы. k — переменная, в данном случае число реально наблюдённых событий в конкретной выборке. Если нужно узнать вероятность наблюдать k₁ событий, это значение подставляется в функцию: ${\displaystyle f(k_{1};\lambda )}$. Не изменяя систему, можно брать множество выборок с разными значениями k, но система всегда характеризуется одним и тем же λ.

Например, пусть имеется радиоактивный образец, испускающий в среднем пять частиц за десять минут; измеряют, сколько частиц испускается за каждый десятиминутный интервал. Измерения дадут разные значения k, и если образец подчиняется статистике Пуассона, то каждое значение k будет встречаться с частотой, определяемой функцией вероятности выше. Однако от измерения к измерению λ остаётся постоянным и равным 5. Если система не меняется, параметр λ не изменяется от измерения к измерению; если же заменить образец на более радиоактивный, λ увеличится.

Другое распространённое распределение — нормальное распределение, параметры которого — среднее μ и дисперсия σ².

В приведённых примерах распределения случайных величин полностью определяются типом распределения (Пуассона или нормальным) и значениями параметров (средним и дисперсией). В этом случае говорят о параметризованном распределении.

Можно использовать последовательность моментов (среднее, среднеквадратичное и т. д.) или кумулянтов (среднее, дисперсия и т. д.) в качестве параметров распределения вероятностей^[7].

В информатике параметр определяется как «ссылка или значение, передаваемое функции, процедуре, подпрограмме, команде или программе»^[2]. Например, имя файла (параметр) передаётся компьютерной программе, которая затем выполняет определённую функцию; то есть программе можно передать имя файла, с которым будет производиться определённое действие.

В программировании обычно различают два понятия параметра, известные как параметры и аргументы, или формально — формальные параметры и фактические параметры.

Например, в определении функции

y = f(x) = x + 2,

x — формальный параметр (параметр) определяемой функции.

При вычислении значения функции для конкретного значения, например

f(3): или, y = f(3) = 3 + 2 = 5,

3 — фактический параметр (аргумент) для вычисления функции. Это конкретное значение, подставляемое вместо формального параметра определённой функции. В обычной речи термины «параметр» и «аргумент» могут путать и использовать некорректно.

Эти понятия более строго рассматриваются в функциональном программировании и его фундаментальных дисциплинах — лямбда-исчислении и комбинаторной логике. Терминология различается в разных языках программирования; некоторые, например C, определяют параметры и аргументы, как указано выше, тогда как язык Eiffel использует альтернативную конвенцию.

В инженерии (особенно при сборе данных) термин параметр иногда свободно употребляется для обозначения отдельного измеряемого элемента. Это использование не всегда последовательно, так как иногда термин канал означает отдельный измеряемый элемент, а параметры — информацию о настройках этого канала.

В общем случае свойства — это те физические величины, которые непосредственно описывают физические атрибуты системы; а параметры — это такие комбинации свойств, которые достаточны для определения отклика системы. Свойства могут иметь любые размерности, в зависимости от рассматриваемой системы; параметры же безразмерны, имеют размерность времени или обратную ей^[8].

Однако термин также может использоваться в инженерных контекстах так же, как и в естественных науках^[9].

В экологических науках, особенно в химии и микробиологии, параметр используется для описания дискретной химической или микробиологической сущности, которой можно приписать значение: обычно концентрацию, но также это может быть логическая сущность (наличие/отсутствие), статистический результат, например 95-й перцентиль, или, в некоторых случаях, субъективная оценка^[10].

В лингвистике слово «параметр» почти исключительно используется для обозначения бинарного переключателя в универсальной грамматике в рамках принципов и параметров^[11].

В логике параметры, передаваемые (или обрабатываемые) открытым предикатом, называются параметрами. Локально определённые внутри предиката параметры называют переменными. Это дополнительное различие важно при определении подстановки (в его отсутствие оговаривается избежание захвата переменных). Другие называют параметры, передаваемые открытым предикатам, свободными переменными, и при определении подстановки различают свободные и связанные переменные^[12].

В теории музыки параметр обозначает элемент, который может быть изменён (сочинён) отдельно от других элементов. Термин употребляется для высоты звука, громкости, длительности и тембра, хотя теоретики или композиторы иногда рассматривают и другие музыкальные аспекты как параметры. Термин особенно распространён в сериализме, где каждый параметр может следовать определённой серии. Пол Лански и Джордж Перл критиковали расширение слова «параметр», поскольку оно не связано напрямую с математическим значением, но термин остаётся распространённым. Он также часто используется в музыкальном продюсировании, где функции устройств обработки звука (например, атака, релиз, соотношение, порог и другие переменные в компрессоре) определяются специфическими для устройства параметрами (компрессор, эквалайзер, задержка и т. д.)^[13].

В фотографии параметрами называют совокупность характеристик, определяющих снимок; при съёмке в ручном режиме эти параметры можно изменять для достижения определённой цели.