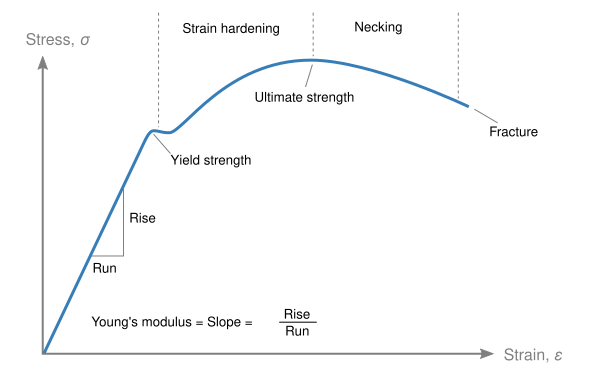
Модуль Юнга

В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.

В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.

Модуль Юнга рассчитывается следующим образом:

${\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}$

где:

• ${\displaystyle F}$ — нормальная составляющая силы,
• ${\displaystyle S}$ — площадь поверхности, по которой распределено действие силы,
• ${\displaystyle l}$ — длина деформируемого стержня,
• ${\displaystyle \Delta l}$ — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина ${\displaystyle l}$).

Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:

${\displaystyle c={\sqrt {\frac {E}{\rho }}},}$

где ${\displaystyle \rho }$ — плотность вещества.

В случае изотропного тела модуль Юнга связан с модулем сдвига ${\displaystyle G}$ и модулем объёмной упругости ${\displaystyle K}$ соотношениями

${\displaystyle G={\frac {E}{2(1+\nu )}}}$

и

${\displaystyle K={\frac {E}{3(1-2\nu )}},}$

где ${\displaystyle \nu }$ — коэффициент Пуассона.

Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости ${\displaystyle M(T)}$ определяется как вторая производная от внутренней энергии ${\displaystyle W(T)}$ по соответствующей деформации ${\displaystyle E(T)={d^{2}W(T) \over d\varepsilon ^{2}}}$ . Поэтому при температурах ${\displaystyle T\leq \Theta _{D}}$ (${\displaystyle \Theta _{D}}$ — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением

${\displaystyle M(T)=M_{0}-M_{1}T-M_{2}T^{2}}$

где ${\displaystyle M_{0}}$ — адиабатический модуль упругости идеального кристалла при ${\displaystyle T\longrightarrow 0K}$; ${\displaystyle M_{1}T}$ — дефект модуля, обусловленный тепловыми фононами; ${\displaystyle M_{2}T^{2}}$ — дефект модуля, обусловленный тепловым движением электронов проводимости^[2].

Значения модуля Юнга для некоторых материалов приведены в таблице.