Биномиальный коэффициент
Биномиа́льный коэффицие́нт в математике — это неотрицательные целые числа, которые появляются в качестве коэффициентов при применении биномиальной теоремы. Как правило, биномиальный коэффициент обозначается парой целых чисел n ≥ k ≥ 0 и записывается как . Он представляет собой коэффициент при xk в разложении бинома в степень: (1 + x)n. Этот коэффициент может быть вычислен по мультипликативной формуле:
или, используя обозначение факториала,
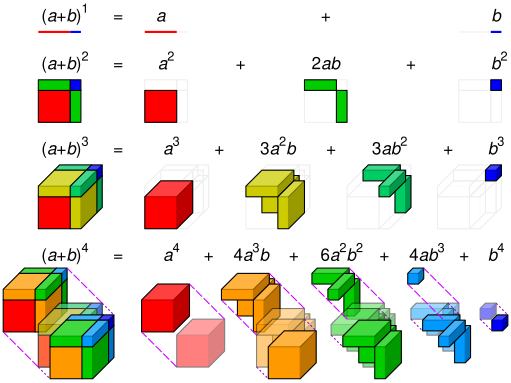
Например, четвёртая степень бинома 1 + x имеет вид:
и биномиальный коэффициент является коэффициентом при x2.
Если расположить числа в строки для {{{1}}}, то получится треугольник Паскаля, удовлетворяющий рекуррентному соотношению:
Биномиальные коэффициенты встречаются во многих областях математики, особенно в комбинаторике. В комбинаторике символ обычно читается как «n выбираем по k», потому что существует способов выбрать неупорядоченное подмножество из k элементов из множества n элементов. Например, есть способов выбрать 2 элемента из множества {1,2,3,4}, а именно: {1,2}, {1,3}, {1,4}, {2,3}, {2,4} и {3,4}.
Мультипликативная формула биномиальных коэффициентов может быть обобщена на для любого комплексного числа z и целого , и многие свойства сохраняются для этого более общего случая.
История и обозначение
Обозначение было введено Андреасом фон Эттингсхаузеном в 1826 году[1], хотя сами числа были известны намного раньше. Около 1150 года индийский математик Бхаскара (санскр. Bhāskara) привёл разъяснение биномиальных коэффициентов в книге «Лилавати»[2].
Альтернативные обозначения включают C(n,k), {}_nC_k, ^nC_k, и другие, в которых C происходит от слова «комбинации» или «выборки» (англ. combinations, англ. choices). Многие калькуляторы используют такие обозначения, поскольку они легко помещаются на однострочном дисплее. Подобные обозначения удобно сравнивать с числами перестановок, обозначаемыми как P(n,k).
Определение и интерпретации
| n\k | 0 | 1 | 2 | 3 | 4 | ⋯ |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | ⋯ |
| 1 | 1 | 1 | 0 | 0 | 0 | ⋯ |
| 2 | 1 | 2 | 1 | 0 | 0 | ⋯ |
| 3 | 1 | 3 | 3 | 1 | 0 | ⋯ |
| 4 | 1 | 4 | 6 | 4 | 1 | ⋯ |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ |
| Первые биномиальные коэффициенты (выравнены по левому краю) | ||||||
Для натуральных чисел (включая 0) n и k, биномиальный коэффициент определяется как коэффициент при мономе Xk в разложении (1+X)^n. Тот же коэффициент возникает (если k \leq n) в биномиальной формуле:
(верно для произвольных элементов x, y коммутативного кольца), — откуда и название «биномиальный коэффициент».
В комбинаторике биномиальный коэффициент выражает количество способов выбрать (без учёта порядка) k объектов из n. Это число можно получить тем же способом, что и определение через разложение бинома, если проанализировать все варианты выбора из n сомножителей выражения (1+X)^n. Существуют и другие комбинаторные интерпретации: например, количество слов из n битов с суммой k равно , а число решений уравнения при неотрицательных целых a_i задаётся формулой .
Вычисление значений биномиальных коэффициентов
Существует несколько способов вычисления без полного разложения бинома или явного перечисления вариантов.
Один из способов — использование рекуррентного соотношения: для целых 1 \leq k < n, с граничными условиями: при n \geq 0.
Эта формула легко объясняется разбиением выбора на те подмножества, которые содержат конкретный элемент, и те, которые не содержат. Для k > n или k < 0 определяют .
Другой метод вычисления биномиальных коэффициентов: где числитель — число способов выбрать упорядоченную последовательность k различных элементов из n, а знаменатель поправляет на неучёт порядка.
Благодаря симметрии по k и n-k, продукт можно ограничить до меньшего из них.
Компактная формула (наиболее используемая в доказательствах): для 0 \leq k \leq n.
Формула также даёт симметрию:
Мультипликативная формула позволяет определять биномиальные коэффициенты для произвольного числа α: для k \in \mathbb{N}.
Обобщённая биномиальная формула: справедлива для произвольных комплексных α, |X| < 1.
Треугольник Паскаля
Треугольник Паскаля строится по правилу:
Строка с номером n содержит числа при 0, …, n — по краям единицы, внутренние числа получаются суммированием двух расположенных выше.
Комбинаторика и статистика
Биномиальные коэффициенты широко используются в комбинаторике:
- — число способов выбрать k элементов из n.
- — количество способов выбрать k элементов с повторениями из n элементов (мультимножества).
- — количество строк из k единиц и n нулей.
- — количество строк из k единиц и n нулей, в которых нет двух подряд стоящих единиц[3].
- Числа Каталана: .
- Биномиальное распределение: .
Биномиальные коэффициенты как многочлены
Для каждого неотрицательного целого k выражение представляет собой многочлен от t с рациональными коэффициентами.
Биномиальные коэффициенты с любым первым аргументом (действительным или комплексным числом) возникают в обобщённых версиях биномиальной теоремы.
Любой многочлен степени не выше d над полем характеристики 0 может быть представлен в виде линейной комбинации биномиальных коэффициентов: .
Основные алгебраические тождества
Из факториальной формулы следуют различные связи соседних биномиальных коэффициентов. Например, .
Сумма биномиальных коэффициентов в строке: Суммы с весом k или k²: .
Также справедлива тождественность Чу-Вандермонда:
Для конкретных значений индексов биномиальные коэффициенты выражаются через числа Фибоначчи: , где F — числа Фибоначчи.
Генерирующие функции
- 0}^{\infty} \binom{n}{k} x^k = (1+x)^n
- Генерирующая по n: 0}^{\infty} \binom{n}{k} y^n = y^k/(1-y)^{k+1
Делимость и сравнения по модулю
Если n — простое, то все внутренние биномиальные коэффициенты делятся на n: . Если n составное, то всегда найдётся значение k, при котором не делится на n.
Делимость и асимптотику биномиальных коэффициентов подробно описывают теорема Куммера и теорема Лукаса. Также биномиальные коэффициенты тесно связаны с наибольшими общими кратными последовательностей целых чисел[4].
См. также
Примечания
Литература
- Ash, Robert B. Information Theory. — Dover Publications, 1990. — ISBN 0-486-66521-6.
- Benjamin, Arthur T. Proofs that Really Count: The Art of Combinatorial Proof / Arthur T. Benjamin, Jennifer J. Quinn. — Mathematical Association of America, 2003. — ISBN 978-0-88385-333-7.
- Bryant, Victor. Aspects of combinatorics. — Cambridge University Press, 1993. — ISBN 0-521-41974-3.
- Graham, Ronald L. Concrete Mathematics: A Foundation for Computer Science / Ronald L. Graham, Donald E. Knuth, Oren Patashnik. — Addison-Wesley Professional, 1994-02. — P. 154–155. — ISBN 0-201-55802-5.
- Shilov, G. E. Linear algebra. — Dover Publications, 1977. — ISBN 978-0-486-63518-7.
- Knuth, Donald E. The Art of Computer Programming, Volume 1: Fundamental Algorithms. — Third. — Addison-Wesley, 1997. — P. 52–74. — ISBN 0-201-89683-4.
- Farhi, Bakir (2007). “Nontrivial lower bounds for the least common multiple of some finite sequence of integers”. Journal of Number Theory. 125 (2): 393—411. arXiv:0803.0290. DOI:10.1016/j.jnt.2006.10.017. S2CID 115167580. Дата обращения 2024-06-20.
|access-date=требует|url=(справка) - Muir, Thomas (1902). “Note on Selected Combinations”. Proceedings of the Royal Society of Edinburgh. Дата обращения 2024-06-20.