Стрелка Пирса
Стре́лка Пи́рса (функция Вебба, отрицание дизъюнкции)[1] — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом в 1880—1881 годах.
Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции ИЛИ-НЕ[2] и задаётся следующей таблицей истинности:
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Таким образом, высказывание «X ↓ Y» означает «(не X) и (не Y)», или, что то же самое, «не (X или Y)». Операция NOR коммутативна: от перемены мест операндов результат операции не изменяется.
Стрелка Пирса, как и штрих Шеффера, образует функционально-полный логический базис для пространства булевых функций от двух переменных. Это означает, что, используя только стрелку Пирса, можно построить все остальные логические операции, например:
- — отрицание;
- — конъюнкция;
- — дизъюнкция;
- — импликация.
В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NOR). С другой стороны, такой подход увеличивает сложность реализующих выражения схем и тем самым снижает их надёжность, а также увеличивает время прохождения сигнала и снижает быстродействие устройства.
Функциональная операция, выполняемая при входах, определяется следующим выражением:
Что важно знать
| Стрелка Пирса | |
|---|---|
| ИЛИ-НЕ, NOR | |
| Определение | |
| Таблица истинности | |
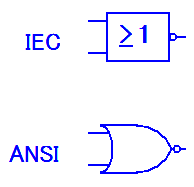
| Логический вентиль |
|
| Нормальные формы | |
| Дизъюнктивная | |
| Конъюнктивная | |
| Полином Жегалкина | |
| Принадлежность предполным классам | |
| Сохраняет 0 | Нет |
| Сохраняет 1 | Нет |
| Монотонна | Нет |
| Линейна | Нет |
| Самодвойственна | Нет |
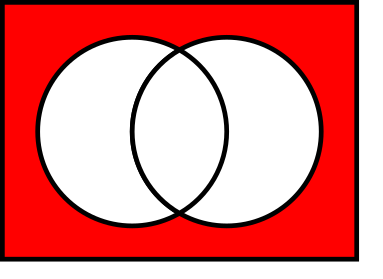
Схемы
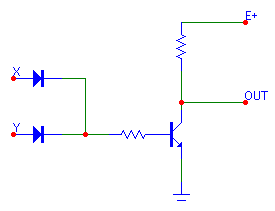
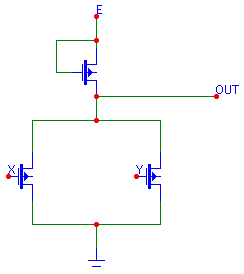
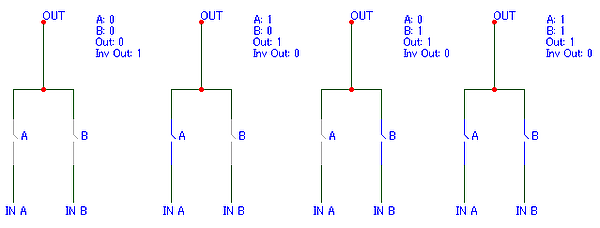
Говоря простым языком, вентиль 2ИЛИ-НЕ — это 2ИЛИ с подключённым к нему инвертором. Для наглядности — ниже приведён пример логической схемы 2ИЛИ-НЕ с выключателями. Как известно, логика 2ИЛИ близка к выражению «или A, или B, или то и другое». Чтобы получить операцию 2ИЛИ-НЕ, результат 2ИЛИ необходимо инвертировать, чтобы получить «не (A или B)». На схеме ниже это выглядит следующим образом: серым отмечены выключатели в состоянии «выключено», синим — в состоянии «включено». На верхней левой схеме оба выключателя находятся в положении «выключено». Таким образом, следуя выражению на выходе, получаем логический 0. Инвертированный результат будет равен 1 и тем самым будет логически удовлетворять выражению «не А, не B». Следующие схемы демонстрируют соответственно «ИЛИ А», «ИЛИ B», «И А, И B» с последующей инверсией результата. Слева представлены варианты реализации вентиля 2ИЛИ-НЕ с помощью диодно-транзисторной логики и с помощью МОП соответственно. Представленная схема на МОП выполнена на однотипных МОП-транзисторах, однако существуют вариант схемы 2ИЛИ-НЕ на комплементарных (дополняющих) МОП-транзисторах. Такую схему получают путём последовательного соединения однотипных транзисторов и параллельного соединения группы транзисторов другого типа.
Литература
- Математический энциклопедический словарь. — М.: «Сов. энциклопедия », 1988. — С. 457—457.
- Белоусов, Аркадий Алгебра логики и цифровые компьютеры
- Д. С. Терещук Логическое моделирование СБИС на переключательном уровне
- Ю. С. Забродин «Промышленная электроника» — С. 221.
- А. О. Маковельский. История логики. — Москва: Кучково поле, 2004. — ISBN 5-86090-081-3.
- Д. Гильберт, В. Aккерман. Основы теоретической логики. — Москва: Иностранная литература, 1947.
- А. И. Попов. Введение в математическую логику. — Ленинград: Ленинградский университет, 1959.