Теория массового обслуживания

Теория массового обслуживания (англ. queueing theory) — это раздел математики, посвящённый изучению очередей и процессов ожидания. Математические модели очередей строятся с целью прогнозирования длины очереди и времени ожидания. Теория массового обслуживания считается частью исследования операций, поскольку её результаты широко используются для обоснования решений о необходимых ресурсах при предоставлении различных услуг.

Истоки теории массового обслуживания связаны с исследованиями Агнера Крарупа Эрланга, который анализировал поступление телефонных вызовов в Копенгагенской телефонной компании. Его работы стали фундаментом для инженерии телетрафика, а сама теория применяется в телекоммуникациях, транспортной инженерии, вычислительной технике, управлении проектами и прежде всего в организации производства, при проектировании заводов, магазинов, офисов и больниц.

Сети массового обслуживания — системы, в которых отдельные очереди соединены маршрутизирующей сетью. На рисунке серверы представлены кругами, очереди — сериями прямоугольников, сеть маршрутизации — стрелками. Обычно задача исследования таких сетей заключается в нахождении стационарного распределения, хотя во многих практических задачах важно и поведение в переходном режиме.

Правописание

В академической литературе чаще встречается написание queueing, а не queuing. Например, один из ведущих журналов области называется Queueing Systems.

Описание

Теория массового обслуживания является одной из ключевых областей науки об управлении. Эта дисциплина позволяет организациям решать широкий круг задач, применяя научные и математические методы. Анализ систем обслуживания опирается на вероятностный подход, а не на детерминированный, что отражается на характеристиках работы системы (либо так называемых эксплуатационных характеристиках). К таким характеристикам относятся вероятность наличия n клиентов в системе, среднее число клиентов в системе, среднее время ожидания в очереди, среднее время пребывания в системе и др Главная цель анализа — вычислить эти показатели для текущей системы и оценить, как они изменятся при различных модификациях. Это помогает принимать решения, повышающие эффективность и снижающие издержки. Основные модели — это системы с одним и несколькими обслуживающими устройствами (сервером или кассами), которые могут учитывать постоянство/случайность времени обслуживания, ограниченность очереди, конечность потока вызовов и другие параметры.

Одноузловые системы обслуживания

Очередь или узел массового обслуживания можно рассматривать как некоторое «чёрный ящик»: задачи (называемые также клиентами или запросами) приходят в очередь, возможно ожидают обслуживания, проходят процесс обслуживания и покидают систему.

Очередь как «чёрный ящик»: задачи поступают и покидают систему.

Однако полностью «чёрным ящиком» узел обслуживания не является: требуется некоторая информация о внутренней структуре. Очередь обслуживают один или несколько серверов, которые по одному подключаются к поступающим задачам. После завершения обслуживания сервер освобождается для нового клиента.

Узел массового обслуживания с тремя серверами: сервер a свободен и получает нового клиента, b занят — обслуживает клиента, c только что завершил обслуживание. Следующий поступивший попадёт к свободному серверу.

Пример: касса в магазине. Покупатели приходят, проходят обслуживание (оплату), уходят. Если касса занята и нет зоны ожидания, клиент уходит (нет буфера); если очередь может включать до n клиентов — очередь с буфером размера n.

Процесс рождения–смерти

См. также: Анализ выживаемости

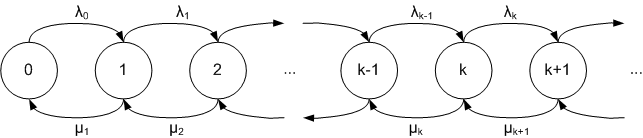
Поведение отдельной очереди (узла обслуживания) обычно моделируется с помощью процесса рождения–смерти, где отмечаются как поступления, так и выбытия клиентов (работ, задач), а состоянием системы является число занятых/ожидающих клиентов k. При поступлении k увеличивается на 1, при выбытии — уменьшается на 1.

Переходы между состояниями происходят с интенситетами поступления $\lambda _{i}$ и обслуживания $\mu _{i}$. В большинстве моделей интенсивности считать постоянными, то есть для всей системы существует среднее $\lambda$ (поступление) и $\mu$ (обслуживание).

Процесс рождения–смерти. В кружках — состояния, которые меняются с теми или иными интенсивностями λ_i и μ_i.

Очередь c одним сервером, интенсивности поступления λ и обслуживания μ.

Уравнения баланса

Стационарные уравнения для процесса рождения–смерти (уравнения баланса):

$\mu _{1}P_{1}=\lambda _{0}P_{0}$

$\lambda _{0}P_{0}+\mu _{2}P_{2}=(\lambda _{1}+\mu _{1})P_{1}$

$\lambda _{n-1}P_{n-1}+\mu _{n+1}P_{n+1}=(\lambda _{n}+\mu _{n})P_{n}$

Например:

$P_{1}={\frac {\lambda _{0}}{\mu _{1}}}P_{0}$

и

$P_{2}={\frac {\lambda _{1}}{\mu _{2}}}P_{1}={\frac {\lambda _{1}\lambda _{0}}{\mu _{2}\mu _{1}}}P_{0}$

В общем виде

$P_{n}={\frac {\lambda _{n-1}\cdots \lambda _{0}}{\mu _{n}\cdots \mu _{1}}}P_{0}=P_{0}\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}$

Требование $\sum _{n=0}^{\infty }P_{n}=1$ даёт:

$P_{0}={\frac {1}{1+\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}}}$

совместно с формулой для $P_{n}$ полностью определяет стационарное распределение.

Обозначения Кендалла

Очереди обычно описываются с помощью обозначения Кендалла в виде A/S/c, где A — распределение поступления, S — распределение времени обслуживания, c — число серверов. Например, M/M/1 — простейшая модель с одним сервером, где входной поток — пуассоновский процесс, времена обслуживания экспоненциальны (M — от Markov). В M/G/1 буква G означает любое распределение вероятностей времени обслуживания.

Пример анализа M/M/1

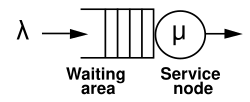
Очередь с одним сервером:

• $\lambda$ — интенсивность поступления (среднее число клиентов в единицу времени)
• $\mu$ — средняя интенсивность обслуживания (обратное среднему времени обслуживания)
• n — число клиентов в системе
• $P_{n}$ — вероятность наличия n клиентов в системе в стационарном режиме

Уравнения баланса:

$\mu P_{1}=\lambda P_{0}$

$\lambda P_{0}+\mu P_{2}=(\lambda +\mu )P_{1}$

$\lambda P_{n-1}+\mu P_{n+1}=(\lambda +\mu )P_{n}$

Отсюда:

$P_{n}=\left(1-\rho \right)\rho ^{n}$, где $\rho ={\frac {\lambda }{\mu }}<1$ — классическое геометрическое распределение.

Простая двухуравневая модель

Базовая система Эрланга (модификация закона Литтла):

$L={\frac {\lambda -\sigma }{\mu }}$,

где λ — интенсивность поступления, σ — интенсивность ухода без обслуживания (отказ, dropout), μ — интенсивность обслуживания, L — средняя длина очереди.

Время ожидания W при экспоненциальных законах определяется как:

${\frac {\mu }{\lambda }}=e^{-W\mu }$

или

$W={\frac {1}{\mu }}\mathrm {ln} {\frac {\lambda }{\mu }}$

Такие модели используются, например, в эпидемиологических задачах.

История

В 1909 году Агнер Краруп Эрланг впервые опубликовал работу по теории массового обслуживания, работая в Копенгагенской телефонной компании. Он применил пуассоновский процесс для моделирования входящего потока вызовов и решил задачу M/D/1 (1917), а затем M/D/k (1920).

• M — «марковский» (memoryless): поступления происходят по пуассоновскому процессу;
• D — «детерминированный»: фиксированное время обслуживания;
• k — число серверов.

При недостатке серверов работы встают в очередь.

Очередь M/G/1 была решена Феликсом Полячеком (1930), а позднее — в вероятностном виде Александром Хинчиным; решение известно как формула Полячека–Хинчина.

С 1940-х теория массового обслуживания активно развивается математиками. В 1953 году Дэвид Джордж Кендалл задал современное обозначение очередей и решил задачу GI/M/k. В 1957 Феликс Полячек исследовал GI/G/1 с помощью интегрального уравнения. Джон Кингман дал оценку среднего времени ожидания в G/G/1 — формула Кингмана.

Леонард Клейнрок применял теорию массового обслуживания к коммутации сообщений (1960-е) и пакетной коммутации (1970-е). Его работы оказали большое влияние на развитие сетей ARPANET — предшественника Интернета.

Разработка матричных методов позволила учитывать фазовые распределения времени обслуживания и прихода.

Модели с связанными орбитами применяются, в частности, в теории беспроводных сетей и обработке сигналов.

Современные приложения теории массового обслуживания охватывают также разработку материальных продуктов с учётом пространственно-временных параметров.

Так, задачи вычисления характеристик для M/G/k-систем во многих случаях до сих пор остаются открытыми.

Дисциплины обслуживания

Возможны различные политики обслуживания клиентов:

Первым пришёл — первым обслужен (FIFO, First come, first served)

Пример работы очереди FIFO

Классический принцип: каждый клиент обслуживается по мере поступления, предпочтение у того, кто ждал дольше.

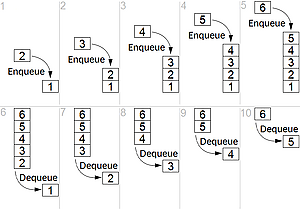
Последним пришёл — первым обслужен (LIFO)

предпочтение новому клиенту с минимальным временем ожидания; модель также называют стеком.

Processor sharing

Совместное разделение ресурсов между всеми клиентами (например, процессорное время делится поровну).

Приоритеты

Особо важные заявки обслуживаются раньше (приоритетные очереди бывают вытесняющими и невытесняющими).

Минимальное время выполнения

обслуживается задача с наименьшим объёмом работы.

Прерываемое обслуживание минимальной задачи

обслуживается задача с минимальным исходным объёмом.

Минимальное оставшееся время

выбирается задача с наименьшим оставшимся временем.

Устройство обслуживания

• Один сервер: одна очередь, один обслуживающий;
• Несколько параллельных серверов с одной очередью: клиенты в общей очереди обслуживаются несколькими серверами;
• Несколько независимых очередей: клиенты сами выбирают, к какому столу встать.

Ненадёжный сервер

отказы происходят случайно (чаще всего по пуассоновскому закону); после отказа требуется настройка или ремонт, клиент ожидает восстановления работы сервера.

Поведение клиентов

• Отказ от входа (balking) — если очередь слишком длинна, клиент не встаёт в очередь;
• Перестановка (jockeying) — клиент меняет очередь, если считает, что в другой обслужат быстрее;
• Ожидание сверх нормы и уход (reneging) — клиент покидает очередь из-за слишком долгого ожидания.

Клиенты, не получившие обслуживание по разным причинам, называются отказниками (dropouts).

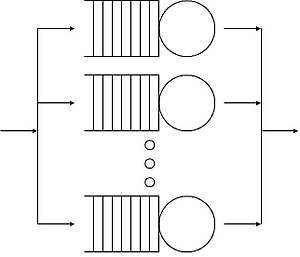
Сети массового обслуживания

Сети массового обслуживания — это системы, состоящие из нескольких взаимосвязанных очередей, между которыми клиенты могут перемещаться после обслуживания. Состояние сети из m узлов описывается вектором из m компонент (x₁, ..., x_m).

Самые простые — тандемные очереди (сети Джексона), для которых найдены эффективные решения (продукт-форма стационарного распределения, анализ средних значений). Если число клиентов в системе постоянно (замкнутая сеть) — работают формулы Гордона–Ньюэлла, которые затем были обобщены для BCMP-сетей, допускающих произвольные режимы обслуживания и модели маршрутизации. Быстрые алгоритмы для вычисления нормирующей константы были предложены Джеффри Бузеном.

Изучались также сети с неоднородным приоритетным обслуживанием (сети Келли), различные типы входных потоков (G-сети по Эролу Геленбе).

Алгоритмы маршрутизации

В дискретных сетях при ограничениях на активность узлов часто используются max-weight-алгоритмы или маршрутизация по обратному давлению для оптимального распределения пропускной способности. Выбор конкретного алгоритма очередей влияет на работу всей сети.

Модель среднего поля

Модель среднего поля рассматривает поведение долей очередей в разных состояниях при бесконечно большом числе узлов. Воздействие остальных очередей на любую фиксированную приближается дифференциальным уравнением. В стационарном случае результат совпадает с изначальной стохастической моделью.

Приближения при высокой загрузке

При больших загрузках систему приближённо описывают с помощью отражённого броуновского движения, орнштейновского процесса и других моделей диффузии. Число измерений процесса соответствует числу очередных узлов.

Детеминированные (флюидные) пределы

Флюидные модели — это определённые (детерминированные) аналоги стохастических моделей, появляющиеся при масштабировании времени и пространства. Для флюидной аппроксимации можно строго доказать устойчивость системы, но возможны ситуации, когда стохастическая сеть устойчива, а её флюидная аппроксимация — нет.

Применение теории массового обслуживания

Теория массового обслуживания широко применяется в компьютерных науках и информационных технологиях. Например, в сетевых устройствах (маршрутизаторах, коммутаторах) анализ очередей позволяет оптимизировать работу при передаче данных и повышать эффективность использования ресурсов.

Принципы теории массового обслуживания актуальны и в повседневной жизни — например, при очередях в магазинах или в общественном транспорте. Понимание закономерностей позволяет оптимизировать процессы и повысить удовлетворённость пользователей. В любой сфере, где возникает ожидание, применимы методы этой теории.

Примечания

Литература

• Gross, Donald. Fundamentals of Queueing Theory / Donald Gross, Carl M. Harris. — Wiley, 1998. — ISBN 978-0-471-32812-4.
• Zukerman, Moshe. Introduction to Queueing Theory and Stochastic Teletraffic Models. — 2013.
• Deitel, Harvey M. An introduction to operating systems. — revisited first. — Addison-Wesley, 1984. — P. 673. — ISBN 978-0-201-14502-1.
• Gelenbe, Erol. Analysis and Synthesis of Computer Systems / Erol Gelenbe, Isi Mitrani. — World Scientific, 2-е изд., 2010. — ISBN 978-1-908978-42-4.
• Newell, Gordron F. Applications of Queueing Theory. — Chapman and Hall, 1971-06-01.
• Leonard Kleinrock. Information Flow in Large Communication Nets, (MIT, Cambridge, 1961)
• Leonard Kleinrock. Information Flow in Large Communication Nets (RLE Quarterly Progress Report, 1961)
• Leonard Kleinrock. Communication Nets: Stochastic Message Flow and Delay (McGraw-Hill, 1964)
• Kleinrock, Leonard. Queueing Systems: Volume I – Theory. — New York : Wiley Interscience, 1975-01-02. — P. 417. — ISBN 978-0-471-49110-1.
• Kleinrock, Leonard. Queueing Systems: Volume II – Computer Applications. — New York : Wiley Interscience, 1976-04-22. — P. 576. — ISBN 978-0-471-49111-8.
• Lazowska, Edward D. Quantitative System Performance: Computer System Analysis Using Queueing Network Models / Edward D. Lazowska, John Zahorjan, G. Scott Graham … [и др.]. — Prentice-Hall, Inc, 1984. — ISBN 978-0-13-746975-8.
• Jon Kleinberg. Algorithm Design / Jon Kleinberg, Éva Tardos. — Pearson, 2013-06-30. — ISBN 978-1-292-02394-6.

Ссылки

• Краткий курс и калькуляторы по теории массового обслуживания (англ.)
• Учебный курс по теории массового обслуживания (Virtamo)
• Страница Майрона Хлынки по теории массового обслуживания (англ.)
• LINE: движок для анализа очередей (англ.)