Цикл Карно

Перейти к материалам ОГЭ/ЕГЭ

РУВИКИ для ОГЭ/ЕГЭ

Читайте краткую версию статьи для подготовки к ОГЭ и ЕГЭ

    
Перейти

Перейти к материалам ОГЭ/ЕГЭ

РУВИКИ для ОГЭ/ЕГЭ

        Читайте краткую версию статьи для подготовки к ОГЭ и ЕГЭ

Перейти

Экспертиза РАН

Проведена экспертиза
Российской Академией Наук

Подробнее

Экспертиза РАН

Проведена экспертиза
Российской Академией Наук

Подробнее

Цикл Карно́ или процесс Карно́ в термодинамике— это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.

Тепловые машины

Николя́ Леона́р Сади́ Карно́
Nicolas Léonard Sadi Carnot
Дата рождения	1 июня 1796(1796-06-01)
Место рождения	Париж
Дата смерти	24 августа 1832(1832-08-24) (36 лет)
Место смерти	Париж
Страна	Франция
Научная сфера	Термодинамика
Известен как	первооткрыватель цикла Карно
Медиафайлы на РУВИКИ.Медиа

Николя́ Леона́р Сади́ Карно́ (фр. Nicolas Léonard Sadi Carnot; 1 июня 1796 (13 прериаля IV года Республики) — 24 августа 1832), более известный как Сади Карно — французский физик и математик, основоположник термодинамики.

Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году. В этой работе Карно сформулировал теорему, названную его именем. Согласно этой теореме, КПД цикла Карно не зависит от природы рабочего тела и конструкции теплового двигателя и является функцией температур нагревателя и холодильника.

Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.

Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах. В реальных тепловых машинах цикл Карно не используют, поскольку практически невозможно осуществить процессы изотермического сжатия и расширения. Кроме того, полезная работа цикла, представляющая собой алгебраическую сумму работ во всех четырёх составляющих цикл частных процессах, даже в идеальном случае полного отсутствия потерь мала по сравнению с работой в каждом из частных процессов, то есть мы имеем дело с обычной ситуацией, когда итоговый результат представляет собой малую разность больших величин. Применительно к математическим вычислениям это означает высокую отзывчивость результата даже на небольшие вариации значений исходных величин, а в рассматриваемом нами случае соответствует высокой чувствительности полезной работы цикла Карно и его КПД к отклонениям от идеальности (потерям на трение). Эта связь с отклонениями от идеальности настолько велика, что с учётом всех потерь полезная работа цикла Карно приближается к нулю.|group=K}}.

Цикл Карно в представлении автора

Вот как описывал рабочий цикл идеальной тепловой машины сам Сади Карно. По сути, эти несколько строк являются своего рода «Манифестом термодинамики», её краеугольным камнем, базой, фундаментом, основанием всех других теоретических изысканий в этой области физики. Описание цикла приведено по «каноническому» переводу трактата Сади Карно на русский язык, выполненному в начале XX века В. Р. Бурсианом и Ю. А. Крутковым с небольшой правкой.

Поясняющий рисунок самого Сади Карно к циклу работы теплового двигателя

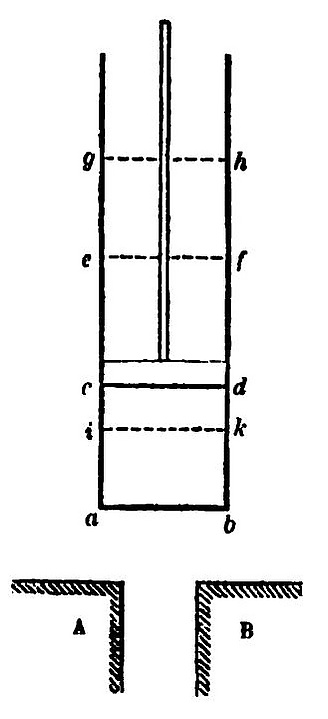
…Вообразим упругий флюид (в переводе — «жидкость»), например, атмосферный воздух, заключённый в цилиндрический сосуд abcd (см. оригинальный рисунок Сади Карно), закрытый подвижной диафрагмой или поршнем cd. Кроме того, предположим два тела A и B, поддерживаемые оба при постоянной температуре, причём A — при более высокой, чем B, затем вообразим следующий ряд операций.

1. Тело A приводится в соприкосновение с воздухом, заключённым в сосуде abcd, или со стенкой сосуда, которая, мы предполагаем, легко пропускает теплород. Благодаря этому соприкосновению, воздух находится при температуре тела A; cd — положение поршня в данный момент.

2. Поршень непрерывно подымается и принимает положение ef. Все время имеет место контакт между телом A и воздухом, который, таким, образом, поддерживается при постоянной температуре во все время разрежения. Тело A даёт теплород, необходимый для поддержания постоянной температуры.

3. Тело A удалено, и воздух больше не находится в соприкосновении с телом, способным его снабжать теплородом; поршень же продолжает своё движение и переходит из положения ef в положение gh. Воздух разрежается, не получая теплорода, и его температура падает. Предположим, что она падает до тех пор, пока не достигнет температуры тела B: в этот момент поршень останавливается и занимает положение gh.

4. Воздух приведён в соприкосновение с телом B; он сжимается движением поршня, который переходит из положения gh в положение cd. Но воздух остаётся при постоянной температуре благодаря контакту с телом B, которому он отдаёт свой теплород.

5. Тело B удалено, продолжается сжатие воздуха; воздух, будучи изолирован, повышает свою температуру. Сжатие продолжается до тех пор, пока воздух не достигнет температуры тела A. Поршень при этом переходит из положения cd в положение ik.

6. Воздух приведён в соприкосновение с телом A; поршень возвращается из положения ik в положение ef; температура остаётся неизменной.

7. Период, описанный в п. 3, повторяется, затем следует 4, 5, 6, 3, 4, 5, 6, 3, 4, 5 и т. д.

После чего Сади Карно делает следующий вывод: В различных положениях поршень испытывает давления более или менее значительные со стороны воздуха, находящегося в цилиндре; упругая сила воздуха меняется как от изменения объёма, так и от изменения температуры, но необходимо заметить, что при равных объёмах, то есть для подобных положений поршня, при разрежении температура будет более высокой, чем при сжатии. Поэтому в первом случае упругая сила воздуха будет больше, а отсюда движущая сила, произведённая движением от расширения, будет больше, чем сила, нужная для сжатия. Таким образом, получится излишек движущей силы, излишек, который можно на что-нибудь употребить. Воздух послужит нам тепловой машиной; мы употребили его даже наиболее выгодным образом, так как не происходило ни одного бесполезного восстановления равновесия теплорода.

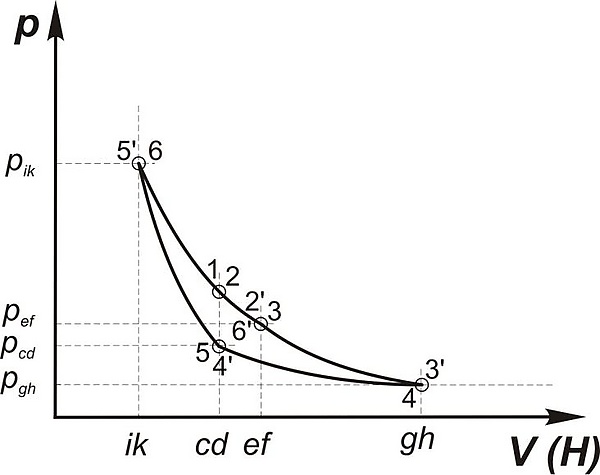
В координатах p(давление) и V (объём) цикл будет выглядеть в виде следующей pV-диаграммы, в которой цифры указывают на пункты описания Сади Карно:

Диаграмма цикла Карно, составленная по описанию автора в цикла в трактате «Размышления о движущей силе огня и о машинах, способных развивать эту силу»

Следует отметить, что сам Сади Карно представлял свой цикл как возможный для использования в реальных паровых машинах.

Описание цикла Карно

Рис. 1. Цикл Карно в координатах T—S

Рис. 2. Цикл Карно в координатах p—V

Рис. 3. Цикл Карно на термодинамической поверхности идеального газа

Пусть тепловая машина состоит из нагревателя с температурой $T_{H}$, холодильника с температурой $T_{X}$ и рабочего тела.

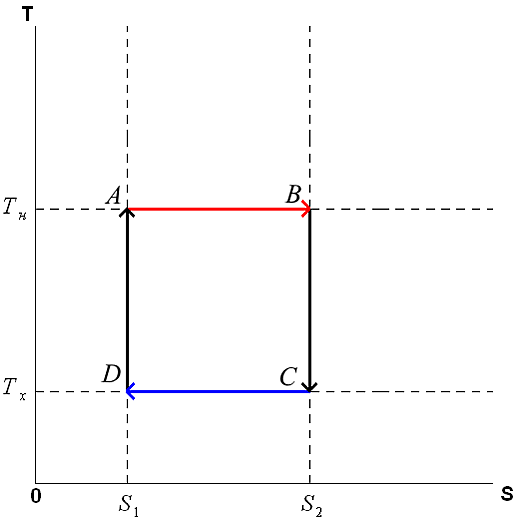
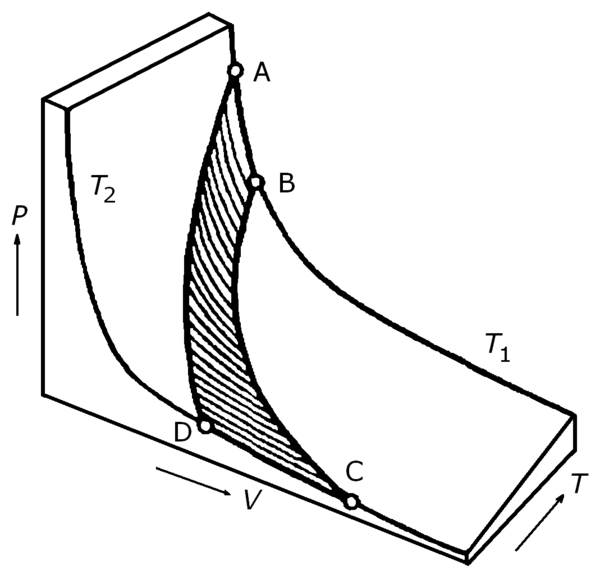
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах $T$ (температура) и $S$ (энтропия).

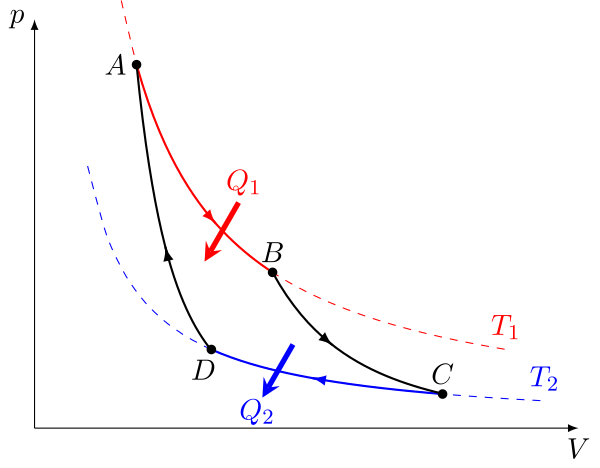
1. Изотермическое расширение (на рис. 1 — процесс A→B). В начале процесса рабочее тело имеет температуру $T_{H}$, то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счёт передачи от нагревателя количества теплоты $Q_{H}$, то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение (на рис. 1 — процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника $T_{X}$, тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие (на рис. 1 — процесс C→D). Рабочее тело, имеющее температуру $T_{X}$, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты $Q_{X}$. Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие (на рис. 1 — процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.

Обратный цикл Карно

В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий: адиабатического сжатия за счёт совершения работы (на рис. 1 — процесс C→B); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 — процесс B→A); адиабатического расширения (на рис. 1 — процесс A→D); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 — процесс D→C).

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

$Q_{H}=\int TdS=T_{H}(S_{2}-S_{1})=T_{H}\Delta S.$

Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

$Q_{X}=T_{X}(S_{2}-S_{1})=T_{X}\Delta S.$

Отсюда коэффициент полезного действия тепловой машины Карно равен

$\eta ={\frac {Q_{H}-Q_{X}}{Q_{H}}}={\frac {T_{H}-T_{X}}{T_{H}}}.$

Первая и вторая теоремы Карно

Основная статья: Теорема Карно (термодинамика)

Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.

Связь между обратимостью цикла и КПД

Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.

Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона, состоящий из двух изобар и двух изотерм.

Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.

См. также

• Термодинамические циклы
• Первое начало термодинамики
• Второе начало термодинамики
• Термодинамическая энтропия
• Термодинамические потенциалы

Примечания

Литература

• Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
• Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. — 2-е изд., испр. — М.: Академия, 2008. — 272 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-4999-1.
• Бэр Г. Д. Техническая термодинамика. — М.: Мир, 1977. — 519 с. (недоступная ссылка)
• Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. — М.—Л.: Госэнергоиздат, 1963. — 280 с.
• Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).
• Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
• Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
• Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. — 2-е изд., испр. и доп. — Новосибирск: Изд-во Носиб. ун-та, 2000. — 608 с. — ISBN 5-7615-0383-2.
• Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
• Кудрявцев П. С. История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
• Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.