Дерево (структура данных)

Это не дерево: присутствуют две несвязанные компоненты (A→B и C→D→E), то есть более одного корня.

Это не дерево: в цикле 1-2-4-3 у узла 4 более одного родителя.

Это не дерево: в цикле B→C→E→D→B у B более одного родителя.

Это не дерево: в цикле A→A узел A является и корнем, и потомком.

Любой линейный список — это тривиальное дерево.

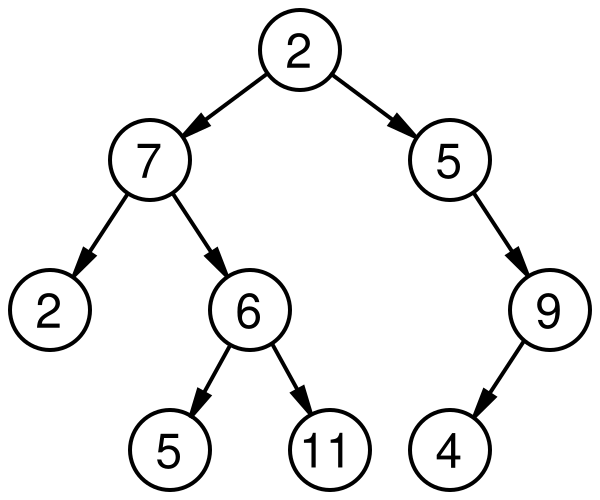
Дерево — это (возможно, нелинейная) структура данных, состоящая из узлов, вершин и рёбер, не содержащая циклов. Дерево без узлов называется пустым или нуль-деревом. Непустое дерево состоит из корневого узла и, возможно, множества других уровней, образующих иерархию.

• Корень: верхний (начальный) узел дерева.
• Потомок: узел, напрямую связанный с другим узлом в направлении от корня.
• Родитель: узел, являющийся прямым предком («обратное» к потомку).
• Братья/сёстры: совокупность узлов с одним родителем.
• Потомок (descendant): узел, достижимый через последовательную цепочку переходов от родителя к потомку.
• Предок (ancestor): узел, достижимый по цепочке переходов от потомка к родителю.
• Лист: узел без потомков.
• Внутренний узел: узел, имеющий хотя бы одного потомка.
• Степень: число поддеревьев (потомков) у узла.
• Ребро: связь между двумя узлами.
• Путь: последовательность узлов и рёбер, соединяющая родителя с одним из потомков.
• Уровень: определяется как 1 + количество рёбер от корня до данного узла.
• Высота узла: количество рёбер на самом длинном пути от узла до листа.
• Высота дерева: высота его корневого узла.
• Глубина: число рёбер от корня дерева до рассматриваемого узла.
• Лес: совокупность из n ≥ 0 попарно непересекающихся деревьев.
• Ветка: путь от корня к любому другому узлу дерева.

Существует различие между деревом как абстрактным типом данных и как конкретной структурой данных, подобно разнице между списком и связным списком. Как абстрактный тип данных дерево содержит значение и потомков, которые, в свою очередь, также являются поддеревьями; значение и потомки дерева рассматриваются как значение корня и поддеревья при нём. Для конечных деревьев допускается либо пустой список потомков, либо возможность наличия пустых деревьев как таковых, при заданной фиксированной степени ветвления (например, дерево с фиксированной степенью, в частности двоичное дерево, если степень равна 2).

Как структура данных, связное дерево — это группа узлов, где каждый узел содержит значение и список ссылок (указателей) на другие узлы (его потомков). Такая структура образует ориентированный граф, поскольку в принципе возможны циклы или множественные ссылки на один и тот же узел, как и в связных списках. Поэтому требуется ограничение: никакие две ссылки не должны указывать на один узел (у каждого узла может быть не более одного родителя; только корень не имеет родителя), а дерево, нарушающее это правило, считается «искажённым» или ошибочным.

Благодаря использованию ссылок в связных деревьях часто подразумевается представление дерева через ссылку на его корень — это стандартная практика при работе с деревьями. Например, вместо пустого дерева часто используют «нулевую ссылку»: дерево формально всегда не пусто, но ссылка на него может быть пустой.

Рекурсивно дерево как абстрактный тип данных определяется как пара: некоторое значение (определённого типа, возможно пустое) и список деревьев (также возможно пустой) — поддеревья при потомках:

t: v [t[1], ..., t[k]]

(Дерево t состоит из значения v и списка других деревьев.)

Более элегантно (через взаимную рекурсию), дерево определяется через лес (список деревьев): дерево состоит из значения и леса (его потомков), а лес — из списка деревьев:

f: [t[1], ..., t[k]]
t: v f

Такое определение актуально для функциональных языков программирования (при референциальной прозрачности); различные деревья независимы друг от друга, это просто списки значений.

Как структура данных, дерево задаётся через узел (корень), включающий значение и список ссылок на другие узлы (иногда допускаются нулевые ссылки и пустые списки):

n: v [&n[1], ..., &n[k]]

(Узел n содержит значение v и список ссылок на других узлов.)

Такая структура реализует ориентированный граф, и для соответствия дереву необходимы дополнительные глобальные ограничения на топологию: не более одной ссылки на любой узел (у каждого — максимум один родитель), ни один узел не может ссылаться на корень. Только корень не имеет родителя, у остальных он один.

Фактически, имея список узлов и, для каждого, список ссылок на детей, нельзя сказать, соответствует ли эта структура дереву без анализа всей глобальной структуры, как это определяется ниже.

В терминах абстрактного типа данных (АТД), абстрактный тип дерева T с элементами типа E определяется с использованием типа леса F (список деревьев) и следующих функций:

значение: T → E

потомки: T → F

пусто: () → F

узел: E × F → T

С аксиомами:

значение(узел(e, f)) = e

потомки(узел(e, f)) = f

В терминах теории типов, дерево — индуктивный тип, заданный конструкторами «пусто» (пустой лес) и «узел» (дерево с корневым значением и потомками).

В совокупности деревовидная структура данных — это упорядоченное дерево, обычно с присвоенными каждому узлу значениями. Более формально, если не допускаются пустые деревья:

• Корневое дерево с ориентацией рёбер от корня (в терминах теории графов — арборесценция):
  • Ориентированный граф.
  • Его неориентированный подлежащий граф — дерево (любые две вершины соединяются единственным простым путём).
  • Задана выделенная вершина (корень).
  • Ориентация рёбер: от корня к потомкам; начало ребра — «родитель», конец — «потомок».

Дополнительно:

• Установлен порядок у потомков каждого узла, и каждому узлу сопоставлено значение.

Часто рассматривают деревья с двумя потомками (допускаются пустые): таковые называют двоичными деревьями.

Допущение пустых деревьев усложняет некоторые определения: дерево с корнем не должно быть пустым, поэтому точнее говорить «пустое дерево ИЛИ корневое дерево такое, что …». Однако пустые деревья делают проще определение деревьев с фиксированной степенью ветвления: двоичное дерево — структура, где каждый узел имеет ровно двух детей (каждый из которых — тоже дерево, возможно пустое). Множество операций над деревом должно включать операцию «разветвления» («вилка»).

Узел — структура, которая может содержать значение или условие либо представлять отдельную структуру данных (в перспективе вырастающую в дерево). Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже него (традиционно дерево рисуют сверху вниз). Узел, имеющий потомка, называется родитель этого потомка (или старший узел). Все узлы, кроме корня, имеют хотя бы одного родителя.

Внутренний узел (также «узел-ветвь» или «внутренний») — любой узел дерева, имеющий потомков. Соответственно, внешний узел (или лист, концевой узел) — узел без потомков.

Самый верхний узел в дереве называют корневым узлом. По одному определению, дерево обязано иметь единственный корень (тогда пустое дерево не допускается); по другому — допускается пустое дерево (не обязательно с корнем). Как старший, корневой узел не имеет родителя. Он служит отправной точкой многих алгоритмов: переход по дереву осуществляется от родителя к потомкам. Некоторые алгоритмы начинают обработку с корня, но сначала посещают листья (сначала получают значения листьев, затем корня). Остальные узлы достижимы по уникальному пути через рёбра («ссылки»). На диаграммах корень располагают вверху. В некоторых типах деревьев (например, кучах) корню придаются особые свойства. Каждый узел дерева может рассматриваться как корень поддерева, порождаемого этим узлом.

Высота узла — длина самого длинного нисходящего пути к листу от этого узла. Высота корня — это высота всего дерева. Глубина узла — длина пути от него до корня (иначе «путь к корню»). Эти понятия важны для работы с самобалансирующимися деревьями (AVL-деревья и пр.): глубина корня — ноль, листья — высота ноль, дерево из одного узла (и корень, и лист) — глубина и высота ноль. Пустое дерево (если допускается) — глубина и высота минус один.

Поддерево дерева T — это дерево, состоящее из некоторого узла в T и всех его потомков в T. Узлы соответствуют поддеревьям (каждому узлу — собственное поддерево из него и всех потомков); поддерево, соответствующее корню, — всё дерево, поддеревья других узлов называют соответствующими поддеревьями (по аналогии с понятием «собственное подмножество»).

Деревья часто изображают на плоскости. Для упорядоченных деревьев возможна их однозначная плоская репрезентация: зафиксировав порядок (например, по часовой стрелке), потомки родителя размещаются в этом порядке, что даёт встраивание (инкрустацию) дерева в плоскость. Обратное тоже верно: такое размещение однозначно определяет порядок потомков.

Если корень помещён наверху (родители выше детей, как в генеалогических деревьях), и все узлы, удалённые от корня на одно и то же число рёбер (уровень), располагаются на одной горизонтальной линии, получается стандартное изображение дерева. В двоичных деревьях левый потомок — левее (это «левый ребёнок»), правый — правее («правый ребёнок»).

Существует множество способов представления деревьев; наиболее распространённые — динамическое хранение каждого узла как структуры с указателями на потомков, родителя или обоих, либо в виде элементов вектора, где отношения определяются по индексам (например, для двоичной кучи).

Двоичное дерево может быть реализовано как список списков (элементы — также списки): голова — левый ребёнок, хвост (оставшиеся элементы) — правый ребёнок. В модификациях типа S-выражений голова списка — значение узла, голова хвоста — левый ребёнок, хвост хвоста — правый.

В общем случае узел может не содержать указателей на родителя, но такую информацию можно включать дополнительно (расширяя структуру или храня отдельно). Альтернативно, обратные ссылки реализуются в данных потомков, как в связных двоичных деревьях.

Если рёбра (к потомкам) интерпретировать как ссылки, то дерево — частный случай графа, а структуру данных дерева можно обобщить до представления направленных графов, устранив ограничение на единственного родителя и отсутствие циклов. Рёбра по-прежнему соединяют пары узлов, однако вместо терминов «родитель» и «потомок» используют, например, «источник» и «приёмник». Существуют различные стратегии реализации: например, граф можно задать так же, как дерево (узлы с данными и списками дочерних ссылок), если считать, что «список детей» — это список ссылок, либо глобально — через структуры типа список смежности.

В теории графов дерево — это связный ациклический граф, причём (если не сказано иное) граф недиректен. Нет однозначного соответствия между деревьями-графами и структурами данных-деревьями. Можно взять любое неориентированное дерево-граф, выделить произвольную вершину как корень, сориентировать все рёбра от корня — получится арборесценция — и задать порядок у всех узлов. Это будет структура данных дерева. При ином выборе корня/порядка получится иной граф.

Потомки узла дерева образуют упорядоченный лес (объединение поддеревьев всех его потомков, или эквивалентно — поддерево узла без корня). Поддеревья естественны для рекурсивных процедур (например, обход в глубину), леса — для корекурсивных (например, обход в ширину).

С помощью взаимной рекурсии лес можно определить как список деревьев (представленных корневыми узлами), а узел дерева состоит из значения и леса (его детей):

f: [n[1], ..., n[k]]
n: v f

Обход элементов дерева по связям «родитель—потомок» называется обходом дерева; соответствующее действие — проход по дереву. Часто при достижении определённого узла выполняется операция. Проход, при котором каждый родитель посещается до посещения его детей, — это проход в прямом порядке; если дети обходятся до родителей — обратный порядок; если левое поддерево, затем сам узел и правое поддерево — симметричный обход. (Последний случай применим к деревьям с двумя потомками — двоичное дерево.) Обход в ширину реализуем через поиск в ширину: уровни дерева обходятся последовательно, сначала корневой узел, затем его прямые дети и их братья, затем внуки и их братья и так далее, пока все элементы не будут посещены.

• Перечисление всех элементов
• Перечисление части дерева
• Поиск элемента
• Добавление нового элемента в заданное место дерева
• Удаление элемента
• Обрезка: удаление целой части дерева
• Прививка: добавление целой части дерева
• Поиск корня для заданного узла
• Представление каждого узла как переменной в памяти с указателями
• Реализация дерева на векторе

• Иерархическое представление данных
• Эффективный поиск информации
• Представление упорядоченных списков данных
• Построение рабочих процессов для композиции цифровых изображений
• алгоритмы маршрутизации