Векторы на плоскости

Ве́ктор — отрезок, для которого указано, какая из его граничных точек считается началом, а какая - концом^[1]. Векторы служат для описания величин, имеющих направление, и широко применяются в геометрии и физике.

Основные понятия

Вектор — направленный отрезок с началом и концом. Обозначается как ${\overrightarrow {AB}}$ , где $A$ — начало, $B$ — конец, или как ${\vec {a}}$ .

Нулевой вектор — вектор, начало которого совпадает с его концом. Его длина равна нулю, направление не определено. На рисунке такой вектор изображается одной точкой и обозначается как ${\overrightarrow {AA}}$ или ${\overrightarrow {0}}$ . Таким образом, любая точка плоскости является вектором.
Длина (модуль) ненулевого вектора ${\overrightarrow {AB}}$ — это длина отрезка $AB$ . Длина вектора ${\overrightarrow {AB}}$ (вектора ${\vec {a}}$ ) обозначается как: $|{\vec {AB}}|$ или ( $|{\vec {a}}|$ ). Длина нулевого вектора считается равной нулю: $|{\vec {0}}|=0$ .
Коллинеарные векторы — векторы, которые лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.
Сонаправленные/противоположнонаправленные векторы — коллинеарные векторы, направленные одинаково/противоположно. Обозначаются как ${\vec {a}}\uparrow \uparrow {\vec {b}}$ / ${\vec {a}}\uparrow \downarrow {\vec {b}}$ соответственно.
Равные векторы — векторы, которые сонаправлены и их длины равны^[2].
Координаты вектора — разность координат конца и начала вектора.

 Если  $A(x_{1},y_{1})$ ,  $B(x_{2},y_{2})$ , то  ${\vec {a}}=(x_{2}-x_{1};\ y_{2}-y_{1})$ .

Длина (модуль) вектора в координатной плоскости

  $|{\vec {a}}|={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$ .

Операции с векторами

Сложение векторов по правилу треугольника и параллелограмма

Сложение векторов

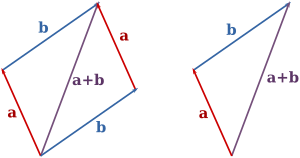
Правило треугольника:

 1. Отложить векторы последовательно, конец первого совмещается с началом второго.
 2. Вектор суммы  ${\vec {c}}={\vec {a}}+{\vec {b}}$  соединяет начало первого вектора с концом второго.

Правило параллелограмма:

 1. Отложить векторы из одной точки.
 2. Построить параллелограмм на этих векторах.
 3. Вектор суммы — диагональ параллелограмма, исходящая из общей точки.

Координатное сложение:

  ${\vec {a}}+{\vec {b}}=(a_{x}+b_{x};\ a_{y}+b_{y})$ .

Вычитание векторов

Правило вычитания:

  ${\vec {a}}-{\vec {b}}={\vec {a}}+(-{\vec {b}})$ , где  $-{\vec {b}}$  — вектор, противоположный  ${\vec {b}}$ .

Координатное вычитание:

  ${\vec {a}}-{\vec {b}}=(a_{x}-b_{x};\ a_{y}-b_{y})$ .

Умножение вектора на число

Увеличивает длину вектора в $|k|$ раз.
Если $k>0$ , направление сохраняется; если $k<0$ , направление противоположно исходному.
Координатная форма:

  $k{\vec {a}}=(ka_{x};\ ka_{y})$ .

Скалярное произведение

Определение:

  ${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}||{\vec {b}}|\cos \varphi$ , где  $\varphi$  — угол между векторами.

В координатах:

  ${\vec {a}}\cdot {\vec {b}}=a_{x}b_{x}+a_{y}b_{y}$ .

Применение:

 Нахождение угла между векторами:
    $\cos \varphi ={\dfrac {{\vec {a}}\cdot {\vec {b}}}{|{\vec {a}}||{\vec {b}}|}}$ .

Применение векторов на плоскости

Решение геометрических задач.
Переход от геометрических объектов к алгебраическим выражениям.
Вычисление расстояний, углов, площадей^[3].

Заключение

Понимание свойств и операций с векторами на плоскости является важной частью изучения математики. Векторы позволяют эффективно решать задачи геометрии и физики, связанные с направленными величинами, и необходимы для успешной подготовки к экзаменам по математике.

Примечания

↑ Атанасян Л. С., Бутузов В. Ф. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений. — М.: Просвещение, 2010. — С. 191. — 384 с.
↑ Атанасян Л. С., Бутузов В. Ф. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений. — М.: Просвещение, 2010. — С. 194. — 384 с.
↑ Атанасян Л. С., Бутузов В. Ф. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений. — М.: Просвещение, 2010. — С. 201. — 384 с.

Литература

Атанасян Л. С., Бутузов В. Ф. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений. — М.: Просвещение, 2010. — С. 191-195. — 384 с.
Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Учебник «Алгебра 7 класс. Учебник для общеобразовательных учреждений» (рус.). — 2013.
Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Учебник «Алгебра 8 класс. Базовый уровень» (рус.). — 2023.
Дорофеев Г. В., Суворова С. Б., Бунимович Е. А., Кузнецова Л. В., Минаева С. С., Рослова Л. О. Учебник «Алгебра. 9 класс» (рус.). — 2014.

[1] Атанасян Л. С., Бутузов В. Ф. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений. — М.: Просвещение, 2010. — С. 191. — 384 с.

[2] Атанасян Л. С., Бутузов В. Ф. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений. — М.: Просвещение, 2010. — С. 194. — 384 с.

[3] Атанасян Л. С., Бутузов В. Ф. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений. — М.: Просвещение, 2010. — С. 201. — 384 с.

[1]

[2]

[3]